1School of Integrated Technology, Yonsei University, Incheon 21983, South Korea
2Korea Aerospace Research Institute, Daejeon 34133, South Korea
†Corresponding Author: Jiwon Seo, E-mail: jiwon.seo@yonsei.ac.kr
Citation: Lee, H., Kim, S., Park, J., Jeong, S., Yu, J., Park, S., Song, J., Choi, H., & Seo, J. 2025, A Comparative Survey of GPS Midi and Reduced Almanacs, Journal of Positioning, Navigation, and Timing, 14, 101-108.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 June, Volume 14, Issue 2, pages 101-108. https://doi.org/10.11003/JPNT.2025.14.2.101
Received on May 11, 2025, Revised on May 19, 2025, Accepted on May 28, 2025, Published on Jun 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
The Global Positioning System (GPS) broadcasts almanac data to assist users in rapidly acquiring satellite signals by providing approximate satellite ephemeris and clock correction information. GPS Civil Navigation (CNAV) messages introduce two types of almanacs: the Midi almanac, identical to the almanac used in the Legacy Navigation (LNAV) message, and the reduced almanac, which is newly defined with a simplified set of parameters. This paper analyzes and compares the Midi and reduced almanacs, focusing on their impact on satellite position estimation accuracy and data transmission efficiency. The results show that the reduced almanac can transmit data for the entire satellite constellation up to seven times faster than the Midi almanac, offering a significant advantage in terms of acquisition time. However, due to its simplified parameter set, the reduced almanac yields lower accuracy in estimating satellite position. When the resulting errors are expressed in angular terms, however, the reduced almanac maintains sufficient precision for identifying satellites above the horizon. These findings suggest that the reduced almanac is suitable for applications where fast signal acquisition is prioritized, such as initial receiver startup, whereas the Midi almanac is more appropriate for scenarios requiring more accurate satellite orbit information.
almanac, Midi almanac, reduced almanac, CNAV
미국의 위성항법시스템인 Global Positioning System (GPS)은 오늘날 군사, 항공, 해운, 차량을 비롯한 다양한 응용 분야에 필수적인 기술로 활용되고 있다. GPS를 통한 위치 추정은 신호 도착 시간(time-of-arrival, TOA)을 기반으로 하는 삼각 측량법을 통해 이루어지며, 이를 위해 모든 GPS 위성은 시각 정보가 포함된 항법메시지(navigation message)를 송신한다 (Misra & Enge 2006).
GPS 항법메시지는 위성 궤도력(ephemeris) 파라미터, 위성 시각 보정(clock correction) 파라미터, 전리층 보정(ionospheric correction) 파라미터, 알마낙(almanac) 등 사용자가 자신의 위치를 계산하는 데 필요한 정보를 포함한다. 이 중, 알마낙은 위성의 대략적인 궤도 정보와 시각 보정 정보를 제공하는 파라미터이다. 위성의 정확한 위치와 시각을 계산하는 데 사용되는 궤도력 및 시각 보정 파라미터와 달리, 알마낙은 위성의 궤도 및 시각 보정 정보 중 일부만을 낮은 정밀도로 제공한다.
사용자는 알마낙 파라미터를 활용하여 warm start 시 GPS 신호 획득(signal acquisition)에 소요되는 시간을 단축할 수 있다 (Misra & Enge 2006, Paonni et al. 2010). 사용자의 대략적인 위치가 알려진 경우, GPS 수신기는 우선 지평선 위의 수신 가능한 위성을 판별한 후, 각 위성의 code delay와 Doppler shift를 추정하여 신호를 획득한다. 이때 알마낙은 위성의 대략적인 궤도 정보와 시각 보정 정보를 제공하여 수신 가능한 위성의 후보군을 효과적으로 좁히는 역할을 한다 (Misra & Enge 2006). 따라서 사용자는 알마낙을 활용함으로써 초기 위치 추정치에 소요되는 시간을 단축할 수 있다.
현재 GPS의 CNAV 메시지에는 두 종류의 알마낙 파라미터(Midi 알마낙과 reduced 알마낙)가 정의되어 있다 (IS-GPS-200N 2022, IS-GPS-705J 2022). 이 중, Midi 알마낙은 기존 LNAV 메시지에 포함되던 알마낙과 동일한 파라미터로, 총 10개의 세부 파라미터를 포함한다. 반면, reduced 알마낙은 GPS 현대화 계획에 따른 CNAV 메시지 도입 (Steigenberger et al. 2015, Lee et al. 2024, GPS Official Website 2025)과 함께 새로 정의된 파라미터로, 총 4개의 세부 파라미터만을 포함한다.
Reduced 알마낙은 포함하는 파라미터 수가 적기 때문에, 전체 위성에 대한 알마낙 정보를 Midi 알마낙 보다 짧은 시간 안에 송신할 수 있다 (IS-GPS-200N 2022, IS-GPS-705J 2022). 그러나 정보가 축소된 만큼, 위성의 대략적인 위치를 예측하는 데 있어 정확도가 떨어질 수 있으며, 이는 GPS 신호 획득 성능에 영향을 미칠 수 있다. 따라서 reduced 알마낙을 사용할 경우, Midi 알마낙과 비교하여 위성 위치 추정 정확도가 어떻게 달라지는지를 분석할 필요가 있다.
이 논문에서는 두 알마낙의 세부 파라미터 구성 차이를 비교하고, 각 알마낙을 통한 위성 위치 예측 정확도 및 파라미터 획득 소요 시간을 분석하였다. 이 논문의 2장에서는 Midi 알마낙과 reduced 알마낙 간 세부 파라미터 구성의 차이를 정리하였고, 3장에서는 각 알마낙 수신에 필요한 시간과 위성 위치 추정 정확도를 분석하였다. 마지막으로, 4장에서는 이 연구의 결론을 제시하였다.
GPS CNAV의 Midi 알마낙은 기존 LNAV 메시지에 포함되던 알마낙 파라미터와 동일한 구성을 가지며, reduced 알마낙에 비해 더 많은 수의 파라미터를 전송한다. 따라서 Midi 알마낙을 이용해 위성 위치를 계산할 경우, reduced 알마낙을 사용할 때보다 더 높은 정확도를 얻을 수 있다.
Midi 알마낙 파라미터는 CNAV 메시지 타입 37에 포함되며, Table 1에 나타난 바와 같이 총 10개의 세부 파라미터로 구성된다 (IS-GPS-200N 2022, IS-GPS-705J 2022). 앞서 언급했듯이, 알마낙 파라미터는 위성 궤도력 및 시각 보정 파라미터의 일부를 낮은 정밀도로 포함한다. 이에 따라, 위성 궤도력 및 시각 보정 파라미터와 Midi 알마낙 파라미터, reduced 알마낙 파라미터의 세부 구성을 비교하면 Table 2와 같다.
Table 1. Midi almanac parameters. All definitions are adapted from the GPS interface control documents (ICD) (IS-GPS-200N 2022, IS-GPS-705J 2022). LSB refers to the least significant bit.
| Parameter | No. of bits | Scale factor (LSB) | Units | Definition |
|---|---|---|---|---|
| toa | 8 | 212 | seconds | Almanac reference time |
| e | 11 | 2−16 | dimensionless | Eccentricity |
| δi | 11 | 2−14 | semi-circles | Relative inclination angle (i0=0.30 semi-circles) |
| $\dot{\Omega}$ | 11 | 2−33 | semi-circles/sec | Rate of right ascension |
| $\sqrt{A}$ | 17 | 2−4 | $\sqrt{meters}$ | Square root of the semi-major axis |
| Ω0 | 16 | 2−15 | semi-circles | Longitude of ascending node of orbit plane at weekly epoch |
| ω | 16 | 2−15 | semi-circles | Argument of perigee |
| M0 | 16 | 2−15 | semi-circles | Mean anomaly at reference time |
| af0 | 11 | 2−20 | seconds | SV clock bias correction coefficient |
| af1 | 10 | 2−37 | sec/sec | SV clock drift correction coefficient |
Table 2. Comparison of broadcast satellite ephemeris and clock correction parameters with Midi and reduced almanac parameters. All definitions are adapted from the GPS ICD (IS-GPS-200N 2022, IS-GPS-705J 2022). The satellite ephemeris and clock correction parameters are based on CNAV, which defines a slightly different parameter set compared to LNAV.
| Parameters | Definitions | Ephemeris & clock correction | Midi almanac | Reduced almanac |
|---|---|---|---|---|
| toe | Ephemeris/almanac data reference time of week | O | O | O |
| $\dot{A}$ | Change rate in semi-major axis | O | X | X |
| ΔA | Semi-major axis difference at reference time | O | O ($\sqrt{A}$) | O (δA) |
| M0-n | Mean anomaly at reference time | O | O (M0) | O (Φ0) |
| en | Eccentricity | O | O (e) | X |
| ωn | Argument of perigee | O | O (ω) | O (Φ0) |
| Δn0 | Mean motion difference from computed value at reference time | O | X | X |
| $\Delta \dot{n}_0$ | Rate of mean motion difference from computed value | O | X | X |
| Ω0-n | Longitude of ascending node of orbit plane at weekly epoch | O | O (Ω0) | O (Ω0) |
| $\Delta \dot{\Omega}$ | Rate of right ascension difference | O | X | X |
| i0-n | Inclination angle at reference time | O | O (δi) | X |
| IDOT | Rate of inclination angle | O | X | X |
| Cis-n | Amplitude of the sine harmonic correction term to the angle of inclination | O | X | X |
| Cic-n | Amplitude of the cosine harmonic correction term to the angle of inclination | O | X | X |
| Crs-n | Amplitude of the sine harmonic correction term to the orbit radius | O | X | X |
| Crc-n | Amplitude of the cosine harmonic correction term to the orbit radius | O | X | X |
| Cus-n | Amplitude of the sine harmonic correction term to the argument of latitude | O | X | X |
| Cuc-n | Amplitude of the cosine harmonic correction term to the argument of latitude | O | X | X |
| af0 | SV clock bias correction coefficient | O | O | X |
| af1 | SV clock drift correction coefficient | O | O | X |
| af2 | SV clock drift rate correction coefficient | O | X | X |
Midi 알마낙 관련 사용자 알고리즘은 위성 궤도력 파라미터를 통해 위성의 위치, 속도, 가속도를 계산하는 데 사용되는 사용자 알고리즘 (IS-GPS-200N 2022, IS-GPS-705J 2022)과 기본적으로 동일하다. 다만, 궤도력 파라미터에는 포함되지만 Midi 알마낙 파라미터에는 포함되지 않은 변수는 모두 0으로 설정하여 계산에 사용한다 (IS-GPS-200N 2022, IS-GPS-705J 2022). 위성 궤도력 파라미터를 통해 위성 위치를 계산하는 사용자 알고리즘을 블록 다이어그램으로 나타내면 Fig. 1과 같다. 또한, Midi 알마낙 파라미터 적용 시 위성 위치 계산 수식의 변화는 Table 3에 정리하였으며, Table 3에 포함되지 않은 위성 위치, 속도, 가속도 계산식은 궤도력 파라미터와 동일하게 적용된다.
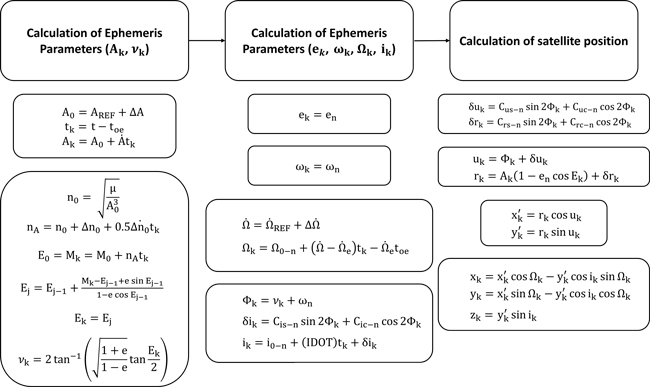
Fig. 1. User algorithm for satellite position calculation using ephemeris parameters. AREF is the reference value of semi-major axis at the reference time (AREF =26,599,710 m), μ is the Earth’s gravitational constant (μ=3.986005×1014 m3/s2), and $\dot{\Omega}$REFis the Earth’s rotation rate ($\dot{\Omega}$REF=7.2921151467×10-5 rad/s). xk , yk , and zk represent the Earth-fixed coordinates of the satellite. All other definitions are provided in Table 2. All equations are adapted from the GPS ICD (ISGPS-200N 2022, IS-GPS-705J 2022).
Table 3. Differences between user algorithms for satellite position calculation using ephemeris parameters and Midi almanac parameters. All equations are adapted from the GPS ICD (IS-GPS-200N 2022, IS-GPS-705J 2022).
| User algorithm using ephemeris parameters | User algorithm using Midi almanac parameters |
|---|---|
| A0 = AREF + ΔA | A0 = AREF |
| Ak = A0 + ($\dot{A}$) tk | Ak = (√A)2 |
| ΔnA = Δn0 + ½ Δṅ0 tk | ΔnA = 0 |
| δuk = Cus-n sin2Φk + Cuc-n cos2Φk | δuk = 0 |
| δrk = Crs-n sin2Φk + Crc-n cos2Φk | δrk = 0 |
| δik = Cis-n sin2Φk + Cic-n cos2Φk | δik = 0 |
| ik = i0-n + (IDOT) tk + δik | ik = i0 (= 0.3 semi-circles) + δi |
| $\dot{\Omega}$= ΩREF + Δ$\dot{\Omega}$ | $\dot{\Omega}$ |
| Ωk = Ω0-n + ($\dot{\Omega}$ − $\dot{\Omega}$e) tk − $\dot{\Omega}$e toe | Ωk = Ω0 + ($\dot{\Omega}$̇ − $\dot{\Omega}$e) tk − $\dot{\Omega}$e toe |
Reduced 알마낙은 Midi 알마낙에 비해 적은 파라미터를 포함한다. 이에 따라, reduced 알마낙은 Midi 알마낙보다 적은 비트를 통해 짧은 시간 내에 전체 위성에 대한 알마낙 정보를 방송할 수 있다.
Reduced 알마낙 파라미터는 CNAV의 메시지 타입 12와 31에 포함되며, Table 4와 같이 총 4개의 세부 파라미터로 구성된다 (IS-GPS-200N 2022, IS-GPS-705J 2022). δA 파라미터는 기준 시각에서의 AREF 값(26,559,710 m)에 상대적인 장반경(semimajor axis) 차(difference)를 의미하며, 위성 궤도의 장반경(A)을 계산하는 데 사용된다. 또한, δA 파라미터는 위성 궤도력 파라미터 중 ∆A에 대응되는 파라미터이다. Ω0 파라미터는 승교점 경도(longitude of ascending node)를 나타내며, 위성 궤도력 파라미터 중 Ω0-n에 대응되는 파라미터이다. 마지막으로, Φ0 파라미터는 기준 시각에서의 적경 편각(argument of latitude)을 나타내며, 이는 평균 근점 이각(mean anomaly; M0 )과 근지점 편각(argument of perigee; ω)의 합과 같다. Φ0 파라미터는 위성 궤도력 파라미터 중 M0-n과 ωn의 합에 대응되며, 위성 위치 계산 사용자 알고리즘에서 현재 시각에서의 적경 편각(Φk ) 대신 사용될 수 있다. 궤도력 파라미터를 이용한 위성 위치 계산 사용자 알고리즘에서는 M0-n, ωn과 함께 전송된 Δn0 , Δ$\dot{n}_0$ , en 파라미터를 통해 정밀하게 계산된 Φk를 얻어서 위치 계산에 사용하지만, reduced 알마낙의 경우 단순히 M0-n과 ωn의 합을 나타내는 Φ0를 통해 Φk를 대신한다 (IS-GPS-200N 2022, IS-GPS-705J 2022).
Table 4. Reduced almanac parameters. All definitions are adapted from the GPS ICD (IS-GPS-200N 2022, IS-GPS-705J 2022). LSB refers to the least significant bit.
| Parameter | No. of bits | Scale factor (LSB) | Units | Definition |
|---|---|---|---|---|
| toa | 8 | 212 | seconds | Almanac reference time |
| δA | 8 | 29 | meters | Relative semi-major axis (Aref = 26,559,710 m) |
| Ω0 | 7 | 2−6 | semi-circles | Longitude of ascending node of orbit plane at weekly epoch |
| Φ0 | 7 | 2−6 | semi-circles | Argument of latitude at reference time (Φ0 = M0 + ω) |
Reduced 알마낙 관련 사용자 알고리즘은 궤도력 파라미터를 통해 위성의 위치, 속도, 가속도를 계산하는 데 사용되는 사용자 알고리즘 (IS-GPS-200N 2022, IS-GPS-705J 2022)과 기본적으로 동일하다. 이 때, Midi 알마낙의 경우와 마찬가지로, 궤도력 파라미터에는 포함되지만 reduced 알마낙 파라미터에는 포함되지 않은 변수는 모두 0으로 설정하여 계산에 사용한다 (IS-GPS200N 2022, IS-GPS-705J 2022). 단, 궤도의 경사각(inclination angle)은 i(55 degrees)+δi (0.0056 semi-circles), 적경 변화율(rate of right ascension, $\dot{\Omega}$)은 -2.6×10-9 semi-circles/second로 고정하여 사용한다 (IS-GPS-200N 2022, IS-GPS-705J 2022).
이번 절에서는 Midi 알마낙과 reduced 알마낙을 사용했을 때, 모든 위성에 대한 전체 알마낙 데이터를 전송하는 데에 소요되는 시간을 분석하였다. 기존 LNAV의 경우, 각 프레임 당 1번부터 5번까지의 subframe을 고정된 순서로 전송하며, 각 subframe의 내용 또한 고정되어 있다 (IS-GPS-200N 2022). 이에 따라, LNAV에서는 모든 위성에 대한 알마낙 파라미터(CNAV의 Midi 알마낙 파라미터와 동일함)를 전송하는데 항상 동일하게 12.5분이 소요된다 (Misra & Enge 2006).
한편, CNAV는 각 패킷의 내용을 유동적으로 교체할 수 있도록 설계되어 있어 보다 유연한 스케줄링이 가능하다. 이로 인해 CNAV에서는 마스터 프레임(master frame)의 구성 방식에 따라 전체 알마낙 데이터 전송에 소요되는 시간이 달라질 수 있다 (Montenbruck et al. 2013).
Fig. 2는 Midi 알마낙이 포함된 L2-CNAV 메시지 타입 37을 나타낸다 (IS-GPS-200N 2022). Fig. 2에서 볼 수 있듯이, 메시지 타입 37을 사용할 경우, 한 패킷에는 위성 1개에 대한 Midi 알마낙 정보만을 포함할 수 있다. Figs. 3과 4는 각각 reduced 알마낙이 포함된 L2-CNAV 메시지 타입 12와 메시지 타입 31을 나타낸다 (IS-GPS-200N 2022). 메시지 타입 12를 사용할 경우, 한 패킷에 최대 위성 7개에 대한 알마낙 정보를 포함할 수 있으며, 메시지 타입 31을 사용할 경우, 한 패킷에 최대 위성 4개에 대한 알마낙 정보를 포함할 수 있다.
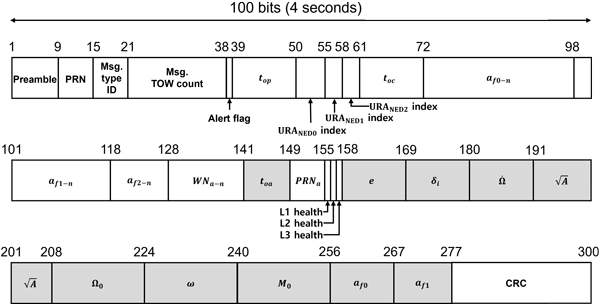
Fig. 2. GPS L2-CNAV message type 37 (reproduced from Fig. 30-10 in ISGPS-200N 2022). Gray shading indicates Midi almanac parameters.
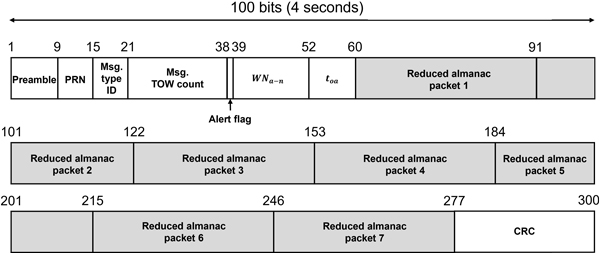
Fig. 3. GPS L2-CNAV message type 12 (reproduced from Fig. 30-10 in ISGPS-200N 2022). Gray shading indicates reduced almanac packets.
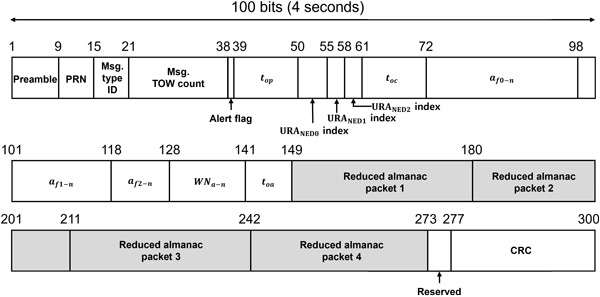
Fig. 4. GPS L2-CNAV message type 31 (reproduced from Fig. 30-10 in ISGPS-200N 2022). Gray shading indicates reduced almanac packets.
이에 따라, reduced 알마낙을 사용할 경우, Midi 알마낙에 비해 최대 7배 빠르게 전체 알마낙 정보를 전송할 수 있다. 예를 들어, Midi 알마낙을 사용할 경우, L2-CNAV를 기준으로 31개의 GPS 위성에 대한 전체 알마낙을 전송하는 데 최소 372초(패킷 31개 × 12초)가 소요된다. 반면, reduced 알마낙은 단 5개의 패킷으로 전체 위성의 알마낙 정보를 전송할 수 있어, L2-CNAV 기준으로 최소 60초(5개 × 12초) 만에 전송을 완료할 수 있다. 참고로, L5-CNAV는 한 패킷의 길이가 6초이므로 (IS-GPS-705J 2022), 동일한 데이터를 전송하는 데 소요되는 시간은 L2-CNAV 대비 절반으로 단축된다.
위와 같이 계산된 데이터 전송 시간은, 다른 항법 메시지 파라미터를 제외하고 알마낙 파라미터만을 전송한다고 가정했을 때의 최소 시간에 해당한다. 앞서 언급한 바와 같이, 실제 CNAV 운용 환경에서는 마스터 프레임의 구성 방식에 따라 알마낙 전송 시간이 달라질 수 있다.
Table 5는 2013년 6월 중 2주간 진행된 CNAV test campaign 당시 사용된 마스터 프레임의 예시를 보여준다 (Montenbruck et al. 2013). CNAV의 메시지 타입 12는 총 7개 위성에 대한 reduced 알마낙 패킷을 포함하므로, 메시지 타입 12를 5번 반복하여 송신하면 모든 GPS 위성에 대한 reduced 알마낙 패킷을 방송할 수 있다. 따라서, Table 5과 같이 마스터 프레임을 설계한 경우, 총 12분 동안 모든 위성에 대한 reduced 알마낙 파라미터를 두차례 반복하여 방송할 수 있다.
Table 5. Sequence of message types in the CNAV master frame during the CNAV test campaign on June 15, 2013 (Montenbruck et al. 2013).
| Sequence | Message type | Sequence | Message type | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 11 | 15 | 30 | 9 | 10 | 11 | 15 | 35 |
| 2 | 10 | 11 | 32 | 33 | 10 | 10 | 11 | 32 | 30 |
| 3 | 10 | 11 | 12 | 35 | 11 | 10 | 11 | 12 | 33 |
| 4 | 10 | 11 | 12 | 30 | 12 | 10 | 11 | 12 | 35 |
| 5 | 10 | 11 | 12 | 33 | 13 | 10 | 11 | 12 | 30 |
| 6 | 10 | 11 | 12 | 35 | 14 | 10 | 11 | 12 | 33 |
| 7 | 10 | 11 | 12 | 30 | 15 | 10 | 11 | 12 | 35 |
| 8 | 10 | 11 | 32 | 33 | |||||
이번 절에서는 Midi 알마낙과 reduced 알마낙을 사용할 경우의 위성 위치 추정 정확도를 분석하였다. GPS interface control documents (ICD) (IS-GPS-200N 2022, IS-GPS-705J 2022)에 따르면, control segment (CS)가 정상적으로 작동하는 경우, LNAV 알마낙(이는 CNAV의 Midi 알마낙과 동일함)은 최소 6일에 한 번, reduced 알마낙은 최소 3일에 한 번 업데이트된다. 이에 따라, 본 논문에서는 알마낙 기준 시각으로부터 최대 6일 경과 시점까지 Midi 및 reduced 알마낙을 기반으로 한 위성 위치 추정 정확도의 변화를 비교하였다.
위성 위치 추정 정확도 분석을 위해, Crustal Dynamics Data Information System (CDDIS)에서 제공하는 GPS 위성의 궤도력 데이터(broadcast ephemeris) (CDDIS 2025)와 United States Coast Guard (USCG) Navigation Center (NAVCEN)에서 제공하는 YUMA 알마낙 데이터 (USCG NAVCEN 2025)를 활용하였다. 2019년 11월 25일자 YUMA 알마낙을 기준으로, 이후 6일 동안의 알마낙 기반 위성 위치 추정 정확도를 분석하였다.
현재 USCG NAVCEN에서는 Midi 알마낙 데이터만을 제공하고 있으며, reduced 알마낙에 대한 공개된 데이터는 확인할 수 없었다. 이에 따라, 본 연구에서는 Midi 알마낙 데이터를 reduced 알마낙 형식에 맞게 가공하여 사용하였으며, 이때 Tables 1과 4에 제시된 각 파라미터의 비트 수 및 스케일 팩터(scale factor)를 고려하였다.
따라서, 본 연구에서 생성한 reduced 알마낙 파라미터는 실제 CNAV 위성에서 전송되는 reduced 알마낙과 정확하게 일치하지 않을 수 있다. 특히, 스케일 팩터 적용 과정에서 소수점 이하 반올림 또는 버림 등 어림 연산이 포함되므로, 이로 인해 추가적인 수치 오차가 유입될 가능성이 존재한다. 이러한 가정과 변환 과정에서의 오차 가능성은 본 연구의 한계로 작용할 수 있다.
Midi 및 reduced 알마낙 기반 위성 위치 추정 정확도를 평가한 결과는 다음과 같다. Fig. 5a는 6일간의 위성 궤도력 파라미터를 바탕으로 계산된 Earth-Centered Earth-Fixed (ECEF) 좌표계에서 PRN 3 위성의 위치를 나타낸다. 또한, Fig. 5b는 동일한 기간 동안 International GNSS Service (IGS)에서 제공하는 정밀 궤도력 (IGS 2025)과 비교하여, 위성 궤도력 파라미터로 계산한 위성 위치의 오차를 나타낸다. Figs. 6a-c는 각각 PRN 1, PRN 3, PRN 17 위성에 대해 위성 궤도력 파라미터로부터 계산된 위성의 위치와, 각 알마낙을 기반으로 추정한 위성 위치 간의 오차를 나타낸다. Fig. 6의 좌측 y축은 해당 위성 위치 추정 오차를 미터 단위로 표현한다. Fig. 6에서 이동 평균(moving average) 필터 적용 시, window size는 24시간으로 설정하였다. 실험 결과, Midi 알마낙을 사용할 경우 수천 미터 수준의 위성 위치 추정 오차가 발생하는 반면, reduced 알마낙을 사용할 경우 수십만 미터에 이르는 큰 위성 위치 추정 오차가 발생하는 것을 확인하였다.
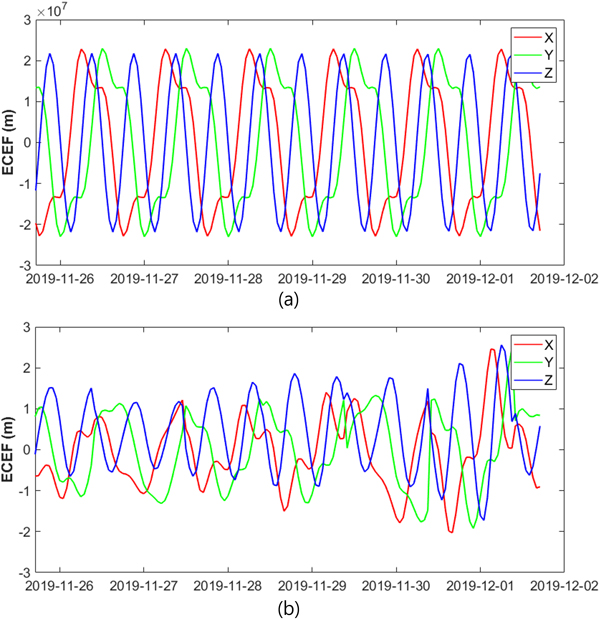
Fig. 5. (a) ECEF position of the PRN 3 satellite computed using the broadcast ephemeris, (b) broadcast ephemeris error evaluated by comparison with the precise orbit provided by the IGS (2025). The IGS final orbit product is used.
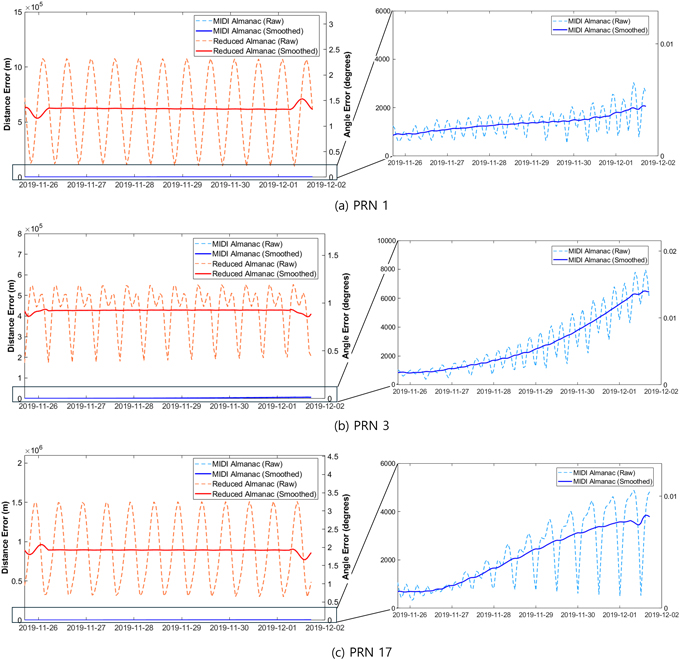
Fig. 6. Satellite position estimation errors calculated using Midi and reduced almanacs for (a) PRN 1, (b) PRN 3, and (c) PRN 17. The right panels show zoomed-in views of the corresponding left panels to highlight detailed variations in the satellite position estimation errors from the Midi almanac.
알마낙 파라미터는 주로 지평선 위에 위치한 수신 가능한 위성을 판별하는 데 사용되므로, 위성 위치 추정 오차를 거리 단위(m)뿐만 아니라 각도 단위(°)로도 평가할 필요가 있다. 따라서 본 논문에서는 Xie et al. (2006)에서 제안된 방법을 적용하여, 위성 위치 오차를 미터에서 도(degree) 단위로 변환하였다. 변환 과정은 Fig. 7과 같다.
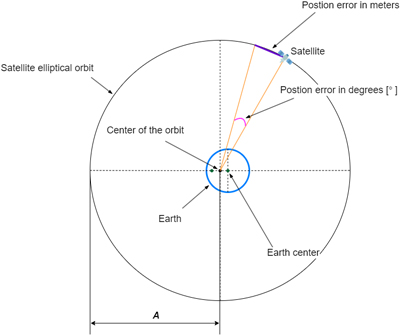
Fig. 7. Satellite position error converted from meters to degrees (reproduced from Fig. 3 in Xie et al. 2006).
Xie et al. (2006)에 따르면, 위성 위치 추정의 각도 오차(angle error, $\theta$)는 거리 오차(distance error, $d$)와 궤도 장반경(A=26,553,409 m)을 바탕으로 Eq. (1)과 같이 계산할 수 있다.
$$\theta = d \times \frac{180}{A \pi}$$
Fig. 6의 우측 y축은 Eq. (1)을 적용하여, 위성 위치 추정 오차를 각도 단위로 변환한 결과를 나타낸다. Fig. 6에서 Midi 및 Reduced 알마낙을 사용하는 두 경우 모두, 위성 위치 추정 오차가 5° 미만의 작은 수준으로 유지됨을 확인할 수 있다. 따라서, 지평선 위의 수신 가능한 위성을 판별하는 용도에는 두 알마낙 모두 충분한 수준의 정확도를 제공할 수 있을 것으로 판단된다.
GPS 항법 메시지의 알마낙은 사용자가 신속히 위치를 추정할 수 있도록 대략적인 위성 궤도력과 시각 보정 정보를 제공하는 파라미터로, GPS CNAV에는 Midi 알마낙과 reduced 알마낙이 정의되어 있다. 본 연구에서는 이 두 알마낙의 세부 파라미터를 분석하고, 이를 활용한 사용자 알고리즘을 조사하였다. 또한, 두 알마낙의 성능을 데이터 전송 소요 시간과 위성 위치 추정 정확도의 관점에서 평가하였다. 평가 결과, 데이터 전송 측면에서는 reduced 알마낙이 Midi 알마낙보다 최대 7배 빠르게 전체 데이터를 전송할 수 있는 것으로 나타났다. 반면, 위성 위치 추정 정확도 측면에서는 reduced 알마낙이 Midi 알마낙보다 다소 낮은 성능을 보였으며, 특히 정확한 위성 위치 추정이 요구되는 상황에서는 그 한계가 분명하게 드러날 수 있다. 다만, 위성 위치 오차를 각도로 환산한 결과, 지평선 위의 수신 가능한 위성을 판별하는 데에는 reduced 알마낙을 사용하더라도 큰 무리가 없는 것으로 확인되었다. 따라서 데이터 전송 효율이 중요한 초기 수신기 구동 단계 등에서는 reduced 알마낙이 유리할 수 있으며, 보다 정확한 위성 위치 정보가 필요한 상황에서는 Midi 알마낙이 더 적합할 수 있다. 이러한 특성을 바탕으로 시스템 설계 및 위성 위치 추정 알고리즘 개발 시, 용도에 따라 알마낙 유형을 선택적으로 활용하는 것이 바람직하다.
본 연구는 과학기술정보통신부의 재원으로 한국연구재단, 무인이동체원천기술개발사업단의 지원을 받아 수행되었음 (2020M3C1C1A01086407). 또한, 본 연구는 2024년 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행되었으며 (RS-2024-00407003, 지상파항법시스템 고도화 기술개발), 우주항공청의 재원으로 지원을 받아 수행된 것임 (과제번호: RS2022-NR067078).
Conceptualization, H. Lee; investigation, H. Lee, S. Kim, and J. Park; resources, H. Lee, S. Kim, J. Park, S. Jeong, J. Yu, S. Park, and J. Song; writing—original draft preparation, H. Lee, S. Kim, J. Park, S. Jeong, J. Yu, and S. Park; writing—review and editing, H. Lee, S. Kim, J. Park, S. Jeong, J. Yu, S. Park, J. Song, H. Choi, and J. Seo; visualization, H. Lee and J. Song; supervision, H. Choi and J. Seo; project administration, H. Choi and J. Seo; funding acquisition, J. Seo.
The authors declare no conflict of interest.
CDDIS 2025, NASA’s Archive of Space Geodesy Data [Internet], National Aeronautics and Space Administration (NASA), cited 2025 Apr 23, available from: https://cddis.nasa.gov/archive/gnss/data
GPS Official Website 2025, Civil Navigation (CNAV) Message [Internet], National Coordination Office for Space-Based Positioning, Navigation, and Timing, cited 2025 Apr 23, available from: https://www.gps.gov/systems/gps/modernization/cnav/
IGS 2025, Precise Orbit and Clock Products [Internet], International GNSS service (IGS), cited 2025 May 16, available from: https://igs.org/products/#orbits_clocks
IS-GPS-200N 2022, Global Positioning System Directorate Systems Engineering & Integration Interface Specification, IS-GPS-200N, Navstar GPS Space Segment / Navigation User Segment Interfaces, USA: Navstar GPS Joint Program Office. https://www.gps.gov/technical/icwg/IS-GPS-200N.pdf
IS-GPS-705J 2022, Global Positioning System Directorate Systems Engineering & Integration Interface Specifi-cation, IS-GPS-705J, Navstar GPS Space Segment / User Segment L5 Interfaces, USA: Navstar GPS Joint Program Office. https://www.gps.gov/technical/icwg/IS-GPS-705J.pdf
Lee, H., Kim, S., Park, J., Jeong, S., Park, S., et al. 2024, A Survey on New Parameters of GPS CNAV/CNAV-2 and Their Roles. Journal of Positioning, Navigation, and Timing, 13, 45-52. https://doi.org/10.11003/JPNT.2024.13.1.45
Misra, P. & Enge, P. 2006, Global Positioning System: Signals, Measurements, and Performance, 2nd ed. (Lincoln: Ganga-Jamuna Press).
Montenbruck, O., Langley, R., & Steigenberger, P. 2013, 2C or Not 2C: The First Live Broadcast of GPS CNAV Messages, GPS World. https://www.gpsworld.com/2c-or-not-2cthe-first-live-broadcast-of-gps-cnav-messages/
Paonni, M., Anghileri, M., Wallner, S., Avila-Rodriguez, J.-A., & Eissfeller, B. 2010, Performance assessment of GNSS signals in terms of time to first fix for cold, warm and hot start, In Proceedings of the 2010 International Technical Meeting of The Institute of Navigation, January 25-27, 2010, San Diego, CA, pp.1051-1066. https://www.ion.org/publications/abstract.cfm?articleID=8885
Steigenberger, P., Montenbruck, O., & Hessels, U. 2015, Performance evaluation of the early CNAV navigation message, Navigation, 62, 219-228. https://doi.org/10.1002/navi.111
USCG NAVCEN 2025, GPS Almanac YUMA Archives [Internet], United States Coast Guard (USCG), cited 2025 Apr 23, available from: https://www.navcen.uscg.gov/archives
Xie, G., Vohra, R., & Yuan, X. 2006, Is It Really Necessary for GPS Receivers to Store Both Satellite Ephemeredes and Almanacs?, In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), 26-29 September 2006, Fort Worth, Texas, pp.1878-1883. https://www.ion.org/publications/abstract.cfm?articleID=6870