1Department of Aerospace Engineering, Korea Advanced Institute of Science and Technology, Daejeon 34141, Korea
2Agency for Defense Development, Daejeon 34060, Korea
†Corresponding Author: Jiyun Lee, E-mail: jiyunlee@kaist.ac.kr
Citation: Kim, J., Kim, N.M., Min, D., Kim, D., & Lee, J. 2025, Development and Analysis of CNAV User Range Accuracy Parameters for WAD-RNSS, Journal of Positioning, Navigation, and Timing, 14, 109-118.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 June, Volume 14, Issue 2, pages 109-118. https://doi.org/10.11003/JPNT.2025.14.2.109
Received on May 10, 2025, Revised on May 15, 2025, Accepted on May 28, 2025, Published on Jun 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Global Navigation Satellite Systems (GNSS) provide worldwide positioning services whereas Regional Navigation Satellite Systems (RNSS) offer services for specific areas. Korea has been developing a RNSS called the Korean Positioning System (KPS), which includes a Wide Area Differential-RNSS (WAD-RNSS) concept that transmits both navigation and correction signals simultaneously. In satellite navigation, Signal-In-Space (SIS) User Range Error (URE) represents errors in navigation signals, while User Range Accuracy (URA) provides a conservative estimate of the standard deviation of the SIS URE. The navigation signals are transmitted in either Legacy Navigation (LNAV) or Civil Navigation (CNAV) formats, with the latter offering advantages including improved flexibility, shorter update intervals, and separate error component representation. CNAV therefore achieves smaller UREs and provides a more sophisticated URA in a format different from that of LNAV. This paper proposes a CNAV URA calculation model for the Korean WAD-RNSS including mathematical expressions for both ElevationDependent (ED) and Non-Elevation-Dependent (NED) URA parameters specifically designed for WAD-RNSS satellite orbital characteristics. Simulation results show that the proposed CNAV URA conservatively bounds the Worst User Location (WUL) URE within the service area. Furthermore, our analysis shows that the proposed CNAV URA allows for a more precise representation compared to the LNAV URA without compromising conservatism. The proposed method can contribute to the development of modernized navigation messages for WAD-RNSS.
global navigation satellite system, user range accuracy, regional navigation satellite system
위성으로부터 송출되는 신호를 활용해 사용자의 위치와 시각 정보를 제공하는 위성항법시스템은 전 지구적 범위의 서비스를 제공하는 글로벌 위성항법시스템(Global Navigation Satellite System, GNSS)과 특정 지역에 최적화된 지역 위성항법시스템(Regional Navigation Satellite System, RNSS)으로 구분된다. 현재 전 세계적으로 운용 중인 GNSS로는 미국의 GPS, 러시아의 GLONASS, 유럽연합의 Galileo, 중국의 BeiDou가 있으며, RNSS로는 일본의 QZSS와 인도의 IRNSS 등이 있다.
RNSS는 특정 지역에 최적화된 가시성과 정확도를 제공하기 위해 정지궤도(Geostationary Earth Orbit, GEO) 위성과 경사 지구동기궤도(Inclined Geosynchronous Orbit, IGSO) 위성을 주로 활용한다. 이러한 궤도 구성은 해당 지역에서 위성 가시성을 극대화하여 도심지나 산악 지형에서도 안정적인 항법 서비스를 가능하게 한다. 대한민국에서도 한반도 지역에 최적화된 위성항법 서비스 제공을 목표로 한국형 위성항법시스템(Korean Positioning System, KPS) 구축을 추진 중이며 (Ahn et al. 2020, Joo & Heo 2020), 이는 기존 GPS와 달리 IGSO 및 GEO 위성을 조합한 위성군 구성을 통해 한반도 지역에서의 우수한 가시성과 정확도를 제공하는 것을 목표로 한다.
최근 Kim et al. (2021)은 KPS의 성능 향상을 위한 새로운 접근법으로 광역 보정 지역 위성항법시스템(Wide Area DifferentialRNSS, WAD-RNSS)을 제안했다. 이 시스템은 지역 위성항법과 광역 보정항법 기술을 통합하여 한반도 및 인근 지역에서 더욱 정밀한 측위 서비스를 제공할 수 있는 발전된 형태의 RNSS 시스템이다. WAD-RNSS는 지역 위성항법시스템의 장점인 우수한 가시성과 광역 보정항법의 높은 정확도를 결합함으로써, 기존 글로벌 GNSS 서비스에 의존하지 않고도 독자적인 고정밀 항법 서비스 구현을 가능하게 한다.
WAD-RNSS와 같은 위성항법시스템이 안정적으로 운용되기 위해서는 시스템의 정확도와 무결성을 보장할 수 있는 항법 메시지 설계가 요구된다. 위성항법시스템의 Signal-In-Space (SIS) 항법 신호는 위성의 궤도력 및 시계 정보 등이 포함된 항법 메시지와 의사거리 측정을 위한 Pseudo Random Noise (PRN) 코드로 구성된다. 이러한 SIS 항법 신호는 우주 공간에서 대기권을 통과하여 사용자에게 도달하는 과정에서 다양한 오차가 발생하는데, 그중 위성 궤도력 및 시계 추정에 기인하는 오차를 SIS User Range Error (URE)라 정의한다.
SIS URE는 통계적으로 0을 평균으로 하는 정규 분포를 따르는 것으로 가정되며, 보수적으로 추정된 SIS URE의 표준편차를 User Range Accuracy (URA)라 한다. URA는 위성 궤도력 및 시계 정보와 함께 항법 메시지를 통해 사용자에게 제공되어, 위성 신호의 예상 오차 범위를 알려줌으로써 위치 결정 과정에서의 무결성 감시와 측정치 가중치 결정에 활용된다. 이처럼 URA는 위성항법 서비스의 정확도와 신뢰성을 평가하는 중요한 지표로, 사용자가 위성항법 신호의 품질을 판단하고 안전한 항법 솔루션을 도출하는 데 핵심적인 역할을 한다. 따라서 WAD-RNSS와 같은 지역 위성항법시스템의 설계에 있어 URA 산출 방법론의 개발은 시스템의 안정적 운용과 서비스 품질 보장을 위한 필수 요소라 할 수 있다.
GPS에서는 Legacy Navigation (LNAV) 또는 Civil Navigation (CNAV) 포맷의 항법 메시지를 제공하며, 각 포맷은 고유한 URA 표현 및 파라미터 산출 방식을 채택하고 있다. LNAV 포맷은 GPS 운용 초기부터 사용되어 왔으며, URA는 4비트 크기로 0~15의 단일 인덱스로 표현된다. U.S. DoD (2020)는 LNAV 포맷의 URA 파라미터 산출식을 공개하였으나, 이는 GPS 위성 궤도에 한정된 수식으로, 다른 궤도를 활용하는 위성군에는 그 특성에 적합한 URA 파라미터 산출식이 적용되어야 한다. 이러한 필요성에 따라 Kim et al. (2025)은 한반도 지역 WAD-RNSS 시스템에 대해 LNAV 형식 기반의 URA 파라미터 산출식을 도출하고, 다양한 운용 시나리오에서 산출된 URA 파라미터 값을 분석하여 그 유효성을 검증하였다.
그러나 LNAV URA는 4비트 크기의 단일 인덱스 표현 방식, 고도각에 따른 방향성 변화 반영의 어려움, 궤도 및 시계 오차를 통합적으로 표현하는 구조 등으로 인해 일정한 제약이 존재한다. GPS 현대화 프로그램의 일환으로 도입된 CNAV 메시지 포맷은 이러한 부분을 개선하여, 더 유연한 데이터 구조, 짧은 정보 갱신 주기, 고도각에 따른 URA 파라미터 세분화 등의 특징을 갖추고 있다. 이러한 CNAV의 발전된 구조는 더 정밀한 URA 제공을 가능하게 한다. 따라서 WAD-RNSS와 같은 지역 위성항법시스템의 성능 향상을 위해서는 LNAV URA와 함께, CNAV URA 파라미터 산출 모델의 개발을 통한 메시지 체계 다양화가 필요하다.
CNAV URA 파라미터 산출 방식에 대한 공식적인 세부 정보는 아직 공개되어 있지 않다. 또한, CNAV의 URA 표현 방식이 LNAV와 상이하기 때문에, 선행 연구 (Kim et al. 2025)에서 제안된 LNAV URA 파라미터 산출 모델을 그대로 적용하는 데 한계가 있다. 이에 본 논문에서는 한반도 지역의 WAD-RNSS 환경에 적합한 CNAV URA 파라미터 산출 모델을 새롭게 제안하며, GEO 및 IGSO 위성의 궤도 특성을 반영한 고도각 의존(ElevationDependent, ED) 및 고도각 비의존(Non-Elevation-Dependent, NED) 파라미터 산출 기법을 함께 제시한다. 제안된 모델의 검증을 위해, WAD-RNSS 시뮬레이션 데이터셋을 바탕으로 CNAV URA를 산출하고, 이를 최악 사용자 위치(Worst User Location, WUL)에서의 URE와 비교하였다. 또한, 기준국 네트워크의 분포에 따른 URE 예측 표준 편차 수준이 CNAV URA 산출 방식의 효용성에 미치는 영향을 분석하였다. 마지막으로, Kim et al. (2025)이 제안한 LNAV URA 파라미터와도 비교하였다. 본 연구는 KPS와 같은 지역 위성항법시스템의 현대화된 항법 메시지 설계에 기여할 것으로 기대된다.
본 논문의 구성은 다음과 같다. 2장에서는 CNAV 메시지의 특징을 설명하며, 3장에서는 CNAV URA의 전달 형식과 ED 및 NED 파라미터에 대해 기술한다. 4장에서는 WAD-RNSS를 위한 CNAV URA 파라미터 산출 방법을 제시하고 검증한다. 5장에서는 WAD-RNSS 시뮬레이션 데이터셋을 바탕으로 LNAV 및 CNAV URA을 산출하고 비교한다. 마지막으로 6장에서는 연구의 결론과 향후 연구 방향을 제시한다.
본 장에서는 GPS 시스템의 Interface Control Document (ICD)에 기술되어 있는 CNAV 항법 메세지에 대한 내용을 간략히 정리하였다 (U.S. DoD 2022a, 2022b). 2.1절에서는 CNAV의 특징을 설명하고, 2.2절과 2.3절에서는 CNAV 항법 메시지로 전달되는 궤도력 파라미터와 시계 보정 파라미터에 대해 각각 기술한다.
CNAV는 기존 LNAV 항법메시지의 제한된 데이터 용량, 낮은 데이터 해상도, 전송 신뢰성을 개선하기 위해 도입되었다. CNAV 메시지는 2014년 4월 28일부터 공식 방송을 개시하였으며, GPS Block IIR-M, IIF 및 III 위성에서 L2C 및 L5 채널을 통해 사용자에게 전달된다.
기존 LNAV 메시지가 5개 서브프레임 구조로 전송되는 반면, CNAV 메시지는 Fig. 1과 같이 300비트 길이의 독립 패킷 단위로 전송되는 패킷 기반 프로토콜로 설계되었다. 각 패킷은 최대 전송 주기만 알려져 있으며, 최대 주기 안에서 전송 간격을 유연하게 설정할 수 있다 (U.S. DoD 2022a). 이러한 패킷 기반 구조는 전송 유연성, 스케줄 제어, 신속한 재송신을 가능케하여 서비스 안정성과 정확도를 크게 향상시킨다 (Noh et al. 2022, Kim et al. 2024).
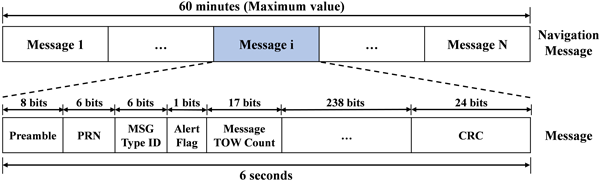
Fig. 1. Structure of CNAV packet (Navipedia 2011).
또한 CNAV 메시지는 전송 전 전진 에러 수정(Forward Error Correction)을 적용하여 수신 측에서 패킷 내의 비트 오류를 교정하고, 이어서 24비트 CRC를 통해 남은 오류를 검출할 수 있도록 설계되었다 (U.S. DoD 2022a). 이러한 향상된 오류 검출 및 복원 능력을 통해 다중경로 및 신호 간섭이 심한 환경에서도 전송 신뢰성을 확보할 수 있다. 2.2절과 2.3절에서는 CNAV 메시지의 주요 구성 요소 중 URE와 URA에 직접적인 영향을 미치는 궤도력 파라미터와 시계 보정 파라미터에 대해 설명한다.
위성의 궤도력 파라미터는 사용자가 위성의 정확한 위치를 계산하는 데 필요한 요소이다. CNAV 메시지는 기존 LNAV 형식과 유사한 궤도력 변수들을 포함하고 있으나, 더 높은 정밀도를 제공하기 위해 비트 할당량이 증가되었으며 일부 새로운 파라미터들도 추가되었다 (Lee et al. 2024). CNAV 메시지에서는 기존 LNAV 메시지와 공유하는 변수들 또한 더 많은 비트 수와 더 작은 단위(scale factor)를 사용하여 정밀도를 개선하였다 (U.S. DoD 2022a). 예를 들어, 경사각(inclination angle)의 경우 LNAV에서는 32비트가 할당되고 scale factor로 2-31 semi-circles를 사용하는 반면, CNAV에서는 33비트가 할당되고 scale factor는 2-32 semi-circles을 사용한다 (U.S. DoD 2022a).
Table 1은 CNAV 메시지에 새롭게 도입된 궤도력 파라미터들을 정리한 것이다. 신규 궤도력 파라미터로는 기준 시점에서 장반경의 차이(ΔA), 장반경 변화율(A · ), mean motion 차이의 변화율(Δn ·), 그리고 right ascension 차이의 변화율(ΔΩ · )이 있다 (U.S. DoD 2022a). 이러한 추가 파라미터들은 위성 궤도의 시간적 변화를 더 정확하게 모델링할 수 있게 하여, 장시간 예측에서 LNAV 대비 향상된 위성 위치 정확도를 제공한다 (U.S. DoD 2022a). 궤도력 파라미터를 적용하는 알고리즘은 U.S. DoD (2022a)의 30.3.3.1.3절에 자세히 기술되어 있다.
Table 1. Newly introduced ephemeris parameters in CNAV message (U.S. DoD 2022a).
| Parameter | Description | No. of bits | Scale factor | Units |
|---|---|---|---|---|
| ΔA | Semi-major axis difference at reference time | 26 | 2−9 | meters |
| $\dot{A}$ | Change rate in semi-major axis | 25 | 2−21 | meters/sec |
| Δ$\dot{n}$ | Rate of mean motion difference from computed value | 23 | 2−57 | semi-circles/sec2 |
| Δ$\dot{\Omega}$ | Rate of right ascension difference | 17 | 2−44 | semi-circles/sec |
Table 2. Satellite clock correction parameters in CNAV message (U.S. DoD 2022a).
| Parameter | Description | No. of bits | Scale factor | Units |
|---|---|---|---|---|
| af0 | SV clock bias correction coefficient | 26 | 2−35 | seconds |
| af1 | SV clock drift correction coefficient | 20 | 2−48 | sec/sec |
| af2 | SV clock drift rate correction coefficient | 10 | 2−60 | sec/sec2 |
| TGD | Inter signal biases between L1 P(Y) and L2 P(Y) | 13 | 2−35 | seconds |
| ISCL1CA | Inter signal biases between L1 P(Y) and L1CA | 13 | 2−35 | seconds |
| ISCL2C | Inter signal biases between L1 P(Y) and L2C | 13 | 2−35 | seconds |
| ISCL5I5 | Inter signal biases between L1 P(Y) and L5I5 | 13 | 2−35 | seconds |
| ISCL5Q5 | Inter signal biases between L1 P(Y) and L5Q5 | 13 | 2−35 | seconds |
CNAV 메시지의 주요 변화 중 하나는 Inter-Signal Correction (ISC) 파라미터의 추가이다. ISC는 서로 다른 주파수 대역 간 하드웨어 지연 차이를 보정하기 위한 파라미터로, 사용자가 더 정확한 시계 보정을 수행할 수 있게 한다 (U.S. DoD 2022a). LNAV에서는 단일 TGD 값만 제공하여 L1 P(Y)와 L2 P(Y) 간의 신호 지연만을 보정할 수 있었다. 반면 CNAV 메시지는 TGD와 더불어 L1, L2, L5 주파수 대역 간 그룹 지연 차이를 보정할 수 있도록 ISCL1CA , ISCL2C , ISCL5I5 등 채널 별 ISC 파라미터를 전송한다 (U.S. DoD 2022a). 위성 시계 보정 파라미터를 적용하는 알고리즘은 U.S. DoD (2022a)의 30.3.3.3절에 자세히 기술되어 있다.
2장에서 언급한 바와 같이 CNAV 메시지의 궤도력과 시계 보정 파라미터는 LNAV에 비해 더 정교하게 모델링되고 더 정밀한 값을 갖는다. 이로 인해 CNAV는 LNAV에 비해 더 작은 위성 궤도 및 시계 오차를 제공할 수 있으며, 더 개선된 URE를 달성할 수 있다 (GPS Official Website 2023). CNAV URA는 기존 LNAV URA의 최소값인 2.4 m보다 더 작은 값까지 표현이 가능하도록 설계되었으며, 고도각에 영향을 받는 ED URA와 영향을 받지 않는 NED URA를 구분하여 전송한다 (U.S. DoD 2022a). 3.1절과 3.2절에서는 GPS 시스템의 ICD에 명시된 CNAV 메시지의 ED와 NED URA에 대해 각각 설명한다 (U.S. DoD 2022a).
위성의 고도각에 따라 변화하는 ED URA는 Scale factor 표현 및 절삭 오차, Along-track 및 Cross-track 위성 궤도 오차를 포함한다 (U.S. DoD 2022a). 이 요소는 -16에서 +15 범위를 갖는 5비트 인덱스로 전송되며, URA 인덱스에 해당하는 구간은 Table 3에서 확인할 수 있다 (U.S. DoD 2022a). 방송된 인덱스는 해당 궤도력 피팅 구간 내에서 유효하며, 피팅 구간과 위성 가시영역(footprint)에 따라 변할 수 있다 (U.S. DoD 2022a). ED URA는 위성 직하점(nadir)에서는 0에 가까우며, 위성 가시영역 가장자리에서 최대값을 가진다. 따라서 ED URA 인덱스는 위성 가시영역 내 최악의 위치(가시영역 가장자리)에서 궤도력 피팅 구간 동안 예상되는 최대 ED URA를 바운드해야 한다 (U.S. DoD 2022a).
Table 3. CNAV URAED index (N) and corresponding ranges (U.S. DoD 2022a).
| URAED Index (N) | URAED (meters) |
|---|---|
| 15 | 6144.00 < URAED (or no accuracy prediction is available) |
| 14 | 3072.00 < URAED ≤ 6144.00 |
| ⋮ | |
| 1 | 2.40 < URAED ≤ 3.40 |
| 0 | 1.70 < URAED ≤ 2.40 |
| −1 | 1.20 < URAED ≤ 1.70 |
| ⋮ | |
| −15 | URAED ≤ 0.01 |
| −16 | No accuracy prediction is available |
사용자는 수신한 URA 인덱스를 활용해 두 가지 URA, 즉 nominal URA와 Integrity Assured URA (IAURA)를 계산할 수 있다 (U.S. DoD 2022a). IAURA는 주어진 URA 구간의 최댓값을 사용하며, SIS 무결성 감시에 주로 사용된다. 반면 nominal URA는 측정치 가중치 결정과 같은 정확도 관련 기능에 활용된다 (U.S. DoD 2022a). 두 값 모두 위성 고도각(E)의 영향 고려하여 cos(E)를 곱한 조정값을 계산함으로써 ED URA를 보다 정확하게 모델링한다 (U.S. DoD 2022a). 본 연구는 IAURA에 집중하여 분석을 진행하며, 이후 본문에서 언급되는 URA는 별도의 언급이 없는 한 모두 IAURA를 의미한다. 조정된 ED URA는 식 (1)과 같으며, nominal URA의 상세 내용은 U.S. DoD (2022a)의 30.3.3.1.1.4절에서 확인할 수 있다.
$$\textit{Adjusted } URA_{ED} = URA_{ED} \cdot \cos(E)$$
위성의 고도각에 영향을 받지 않는 NED URA는 scale factor 표현 및 절삭 오차, 시계 보정 오차, ISC 오차, radial 위성 궤도 오차, 비등방성 안테나 오차, 신호 왜곡 오차 등을 포함된다 (U.S. DoD 2022a). URANED는 시간에 대한 2차 다항식으로 모델링되며, 각 항의 계수 URANED0, URANED1 및 URANED2가 CNAV 메시지로 방송된다. URANED0 인덱스는 URAED와 마찬가지로 -16에서 +15 범위를 갖는 5비트 인덱스로 전송되고 Table 4에 따라 URA 값으로 변환된다 (U.S. DoD 2022a).
Table 4. CNAV URANED0 index (N) and corresponding ranges (U.S. DoD 2022a).
| URANED0 Index (N) | URANED0 (meters) |
|---|---|
| 15 | 6144.00 < URANED0 (or no accuracy prediction is available) |
| 14 | 3072.00 < URANED0 ≤ 6144.00 |
| ⋮ | |
| 1 | 2.40 < URANED0 ≤ 3.40 |
| 0 | 1.70 < URANED0 ≤ 2.40 |
| −1 | 1.20 < URANED0 ≤ 1.70 |
| ⋮ | |
| −15 | URANED0 ≤ 0.01 |
| −16 | No accuracy prediction is available |
URANED1과 URANED2 인덱스는 각각 0에서 7 범위의 3비트로 전송되며, 각 인덱스는 구간 변환이 아닌 식 (2, 3)에 따라 URA 값으로 변환된다. 방송된 인덱스는 해당 궤도력 피팅 구간 내에서 유효하며, 위성 가시영역 내 최악의 위치에서 예상되는 최대 NED URA를 바운드해야 한다 (U.S. DoD 2022a).
$$URA_{NED1} = \frac{1}{2^{N_1}} \; (\text{meters/second}), \\
\text{where } N_1 = 14 + URA_{NED1} \text{ Index}.$$
$$URA_{NED2} = \frac{1}{2^{N_2}} \; (\text{meters/second}^2), \\
\text{where } N_2 = 21 + URA_{NED2} \text{ Index}.$$
수신기는 전송된 세 개의 NED URA 인덱스를 활용해 식 (4)와 같이 Adjusted URANED를 계산할 수 있다. t는 GPS 시간(초), 은 GPS 주 번호이며, 과 는 Clock, Ephemeris, Integrity (CEI) 피팅 기준 시각을 나타낸다. 는 CEI 데이터 경과 시간을 의미하며, 가 93,600 초(26 시간) 이하일 때는 1차 항만, 이를 초과하면 2차 항까지 포함해 URANED를 계산한다. 여기서 26 시간은 GPS의 연장 운영(extended navigation) 모드에서 허용된 최대 피팅 구간이다 (U.S. DoD 2022a).
$$\textit{Adjusted } URA_{NED} =
\begin{cases}
URA_{NED0} + URA_{NED1} \cdot \Delta t, & \Delta t \leq 93{,}600 \text{ seconds}, \\
URA_{NED0} + URA_{NED1} \cdot \Delta t + URA_{NED2} \cdot (\Delta t)^2, & \Delta t > 93{,}600 \text{ seconds},
\end{cases} \\
\text{where } \Delta t = t – t_{OP} + 604{,}800 \cdot (WN – WN_{OP})$$
본 절에서는 WAD-RNSS 환경에 적합한 CNAV URA 산출 방법론을 제안한다. 또한, 제안된 방법론을 WAD-RNSS 위성의 정밀 궤도력 데이터셋에 적용하여 CNAV URA를 산출하고, WUL URE와의 비교를 통해 그 타당성을 검증한다.
CNAV URA는 CNAV 항법 정보의 정확도를 나타내는 핵심 지표 중 하나로, 고도각에 영향을 받는 ED URA와 그렇지 않은 NED URA로 구성된다. 항법 메시지 갱신 이후 시간이 경과함에 따라 위성의 궤도 및 시계 오차가 점진적으로 증가하면서 URE도 함께 증가한다. 따라서 URA는 예측 표준편차로서 다음 메시지 갱신 시점까지 발생 가능한 URE를 보수적으로 바운드하도록 설계된다.
Kim et al. (2025)는 식 (5)와 같이 WAD-RNSS의 LNAV URA 산출식을 제안하였다:
$$URA_{LNAV} = \sqrt{ \frac{1}{36} \left( \sigma_A^2(T) + \sigma_C^2(T) \right) + \sigma_R^2(T) + \sigma_T^2(T) + \sigma_m^2 }$$
여기서 $\sigma_{\scriptscriptstyle A}$, $\sigma_{\scriptscriptstyle C}$, $\sigma_{\scriptscriptstyle R}$는 Along-track, Cross-track, Radial 궤도 오차의 예측 표준편차, $\sigma_{\scriptscriptstyle T}$는 위성 시계 오차의 예측 표준편차, $\sigma_m$은 기타 모델링 오차의 표준편차를 나타낸다. 예측 표준편차는 방송된 항법 메시지의 최대 피팅 기간 또는 최대 유효 기간에 해당하는 시각($T$)에서 예측되는 표준편차를 의미한다 (Rivers 2000). GPS LNAV URA 산출 식에서는 GPS 위성의 운용 고도 및 가시영역을 고려하여 수평(Along/Cross-track) 궤도 오차의 투영 계수를 1/16으로 설정하였다. 반면, 한반도 지역 WAD-RNSS 위성의 고도는 GPS 위성보다 상대적으로 높고 가시영역은 좁기 때문에 Kim et al. (2025)에서는 식 (5)와 같이 수평 궤도 오차의 투영 계수를 1/36로 조정하였다.
CNAV URA는 식 (1)의 Adjusted URAED와 식 (4)의 Adjusted URANED의 제곱합 제곱근으로 계산되며, 식 (6)과 같다:
$$URA_{CNAV} = \sqrt{( \textit{Adjusted } URA_{ED})^2 + ( \textit{Adjusted } URA_{NED})^2 }$$
여기서 URAED는 위성의 고도각에 따라 변화하는 오차 성분을 모델링하며, 수평 궤도 오차가 주요 요소이다. 본 연구에서는 식 (7)과 같이 URAED를 설정할 것을 제안한다:
$$\frac{1}{6} \sqrt{ \sigma_A^2(T) + \sigma_C^2(T) } = URA_{ED}$$
식 (7)의 좌변은 수평 궤도 오차가 최대로 투영되는 WUL에 대한 값이며, LNAV URA는 이 값을 WUL 이외의 모든 고도각에 동일하게 적용한다. 반면 CNAV URA는 고도각이 높아질수록 사용자에게 투영되는 오차가 감소한다는 점을 반영하여, 식 (1)과 같이 ED URA에 고도각 보정을 적용한다. 이때 LNAV의 수평 궤도 오차 항을 URAED로 설정하면, Adjusted URAED는 어떤 고도각에서도 실제 투영 오차를 보수적으로 바운드할 수 있게 된다. 따라서 식 (7)을 만족하면 URAED는 WUL에서는 LNAV와 동일하며, 그 외 위치에서는 고도각 영향을 반영해 LNAV보다 작으면서도 보수적인 URA를 제공할 수 있다.
URANED는 위성의 고도각과 무관한 오차 성분을 모델링하며, 주로 시계 오차와 Radial 궤도 오차가 주요 요소이다. 본 연구에서는 식 (8)과 같이 URANED를 설정할 것을 제안한다.
$$\sqrt{ \sigma_R^2(\Delta t) + \sigma_T^2(\Delta t) + \sigma_m^2 } = URA_{NED}$$
식 (8)의 좌변은 LNAV URA의 Radial 궤도, 시계 및 모델링 오차의 표준편차를 제곱합의 제곱근한 것이다. 이를 만족하도록 URANED를 결정하면, Adjusted URANED는 모든 예측 시간에 대해 Radial 궤도, 시계 및 모델링 오차를 바운드할 수 있다:
$$URA_{NED} \leq URA_{NED0} + URA_{NED1} \cdot \Delta t, \quad \forall \Delta t \in [0, T]$$
예측 시간이 93,600초를 초과하는 구간의 경우, 2차항을 포함한다:
$$URA_{NED} \leq URA_{NED0} + URA_{NED1} \cdot \Delta t + URA_{NED2} \cdot (\Delta t)^2, \quad \Delta t \in [93{,}600, T]$$
결과적으로 URAED 인덱스는 Table 3에 따른 구간별 인덱싱으로 결정된다. 반면, URANED 인덱스는 먼저 식 (8)의 URANED를 계산한 후, 이를 가장 타이트하게 바운드할 수 있는 NED URA 인덱스 조합을 결정한다. 이때 URANED0는 Table 4를 따르며, URANED1과 URANED2는 각각 식 (2, 3)에 따라 인덱스로 변환된다. 본 연구에서는 가능한 모든 조합을 전수 조사하여 해당 시간 범위 내에서 URANED을 가장 타이트하게 바운드하는 최적의 조합을 선택하였다. Fig. 2는 식 (6-10)에 기반한 CNAV URA 산출과 관련된 변수들의 관계를 개념적으로 도식화한 것이다. 이는 본 연구에서 제안한 방식으로 ED와 NED URA 값이 적절히 설정된다면, 최종 CNAV URA가 모든 고도각 및 시간 조건에서 실제 URA를 보수적으로 바운드하도록 설계되었음을 보여준다. 실제 데이터를 기반으로 처리한 결과는 4.2절에서 제시하였다.
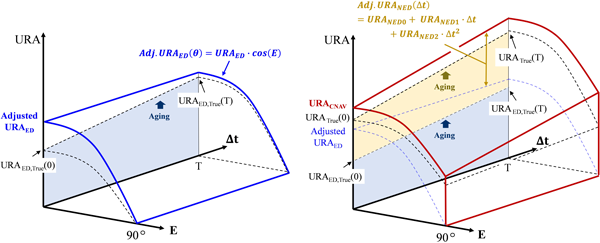
Fig. 2. Visualization of CNAV URA components and their dependence on elevation angle (E) and prediction time (Δt). The left panel illustrates the ElevationDependent (ED) component, with the blue line representing Adjusted URAED . The right panel shows the combined ED and Non-Elevation-Dependent (NED) components, with the solid red line representing the final URACNAV . URAED,True (0) and URAED,True (T) indicate the true ED URA values at prediction times 0 and T, respectively, while URATrue (0) and URATrue (T) denote the true values of the final URA at those times.
본 연구에서는 scale factor 표현 및 절삭 오차, 비등방성 안테나 패턴 오차, 신호 변형에 의한 오차는 다루지 않았으나, 실제 cm급 정밀도의 URA 구현을 위해서는 이들 오차 요인에 대한 추가적인 연구가 필요할 것이다.
본 절에서는 개발된 방법론의 유효성을 검증하기 위해 WAD-RNSS 데이터셋을 활용하여 제안된 기법을 통해 산출된 CNAV URA 값과 실제 URE를 비교 분석한다. 본 연구에서는 Kim et al. (2025)에서 활용한 WAD-RNSS 시스템 시뮬레이션 데이터셋을 동일하게 적용하였다. 이 데이터셋은 총 48시간(24시간 결정 구간, 24시간 예측 구간)에 대한 궤도 및 시계 오차 정보를 포함하며, 국내 기준국만 사용한 경우와 국내외 기준국을 모두 활용한 두 가지 시나리오로 구성되어 있다. 데이터셋의 세부 사항은 Park et al. (2023)과 Kim et al. (2025)에 상세히 기술되어 있다. 해당 연구에서는 한반도 지역에 최적화된 3개의 GEO 위성과 4개의 IGSO 위성으로 구성된 위성군에 대한 시뮬레이션을 수행하였다. 특히, 위성 시계 모델링에는 루비듐 원자시계 특성을 반영한 Galleani 모델이 적용되었으며, 지상 기준국 시계는 세슘 원자시계의 특성을 고려한 모델이 활용되었다 (Park et al. 2023). 이러한 구성을 통해 얻은 궤도 및 시계 오차의 결정 및 예측 결과를 본 연구의 검증에 활용하였다.
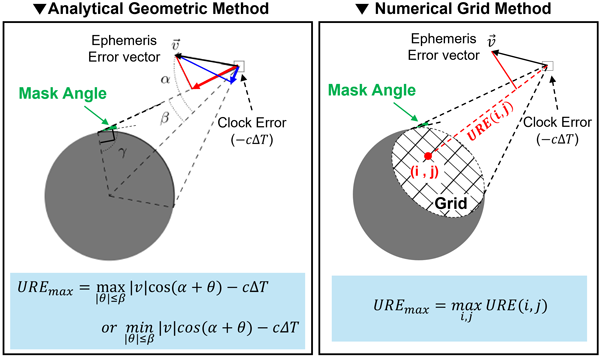
Fig. 3. Worst user location URE derivation: Analytic geometric (right) and numerical grid method (left) (Heng et al. 2012, Kim et al. 2025). Here, v is the ephemeris error vector, and cΔT is the clock error. In the analytical method, α is the angle between the beam centerline and the error vector, while β is the beamwidth angle. θ is the user location angle relative to the centerline. In the numerical grid method, URE(i, j) is the computed URE at each grid point within the beamwidth constrained by the mask angle. The maximum URE corresponds to the worst user location.
검증 과정에서는 위성 가시영역 내 최대 오차를 나타내는 WUL URE를 기준으로 적용하였다. WUL URE는 Fig. 3에 제시된 바와 같이 Heng et al. (2012)의 연구를 기반으로 두 가지 방식으로 산출할 수 있다. 첫째, 해석적 기하법은 위성 가시영역 가장자리에 위치한 사용자를 최악 조건으로 간주하여 위성 위치 오차를 해당 위치로 투영함으로써 WUL URE를 기하학적으로 계산한다. 둘째, 수치적 격자법은 가시영역 전체를 격자로 분할하여 각 지점에서의 URE를 계산한 후 최댓값을 WUL URE로 결정하는 방식으로, 격자 간격에 따라 정확도가 달라질 수 있다.
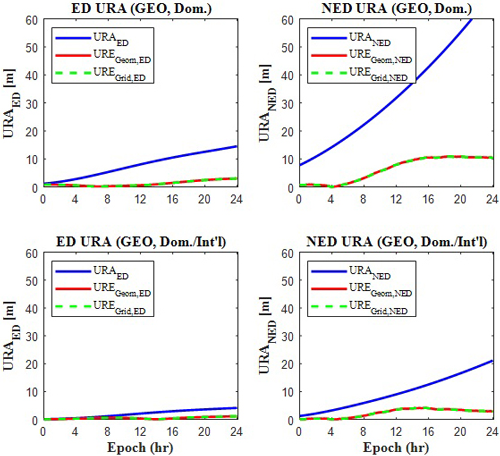
Fig. 4. Comparison of the proposed URAED and URANED with the ED and NED components of the worst user location UREs for GEO satellite.
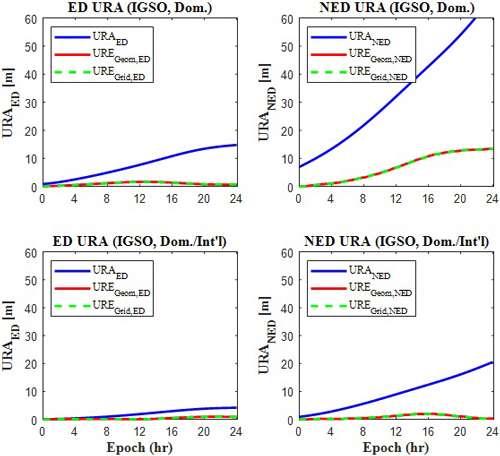
Fig. 5. Comparison of the proposed URAED and URANED with the ED and NED components of the worst user location UREs for IGSO satellite.
Figs. 4와 5는 본 연구에서 제안한 URAED, URANED와 WUL URE의 ED 및 NED 성분을 비교한다. Fig. 4는 GEO에 대해, Fig. 5는 IGSO에 대한 결과이다. 그래프의 Dom.은 국내 기준국만 사용한 경우, Dom./Int’l은 국내외 기준국을 모두 사용한 경우이다. 그래프의 URAED와 URANED는 각각 식 (7)과 (8)에 따라 계산되었다. UREGeom은 해석적 기하법으로 계산된, UREGrid는 수치적 격자법으로 계산된 WUL URE이다. 여기서 WUL URE의 ED 성분은 수평 궤도 오차를, NED 성분은 시계 오차, Radial 궤도 오차, 그리고 모델링 오차를 포함한다.
본 분석에서는 보수적 검증을 위해 모델링 오차($\sigma_m$ = 0 m)는 제외하였으며, 실제 운용 환경에서는 해당 오차가 존재하므로 실제 URA 값은 더 증가하게 된다. Figs. 4와 5에 따르면, 제안된 URAED와 URANED는 모든 예측 구간에서 WUL URE를 바운드하고 있다. 결과적으로, 본 연구에서 제안한 CNAV URA는 WAD-RNSS 위성 가시영역 내 모든 사용자의 SIS URE를 바운드하며, 실제 운용 환경에서도 신뢰성 있게 적용 가능할 것으로 판단된다.
추가 분석 결과, Figs. 4와 5에서 URANED가 URAED보다 전반적으로 큰 값을 보였다. 이는 CNAV URA 산출 시 NED URA의 비중이 더 크다는 것을 의미한다. 또한, 해석적 기하법과 수치적 격자법으로 계산한 WUL URE 값은 거의 일치했는데, 이는 두 방식 모두 위성 가시영역 가장자리에서 최악 사용자 위치를 도출했기 때문이다. 마지막으로 국내외 기준국을 함께 사용하는 경우에 비해 국내 기준국만 사용하는 경우 URA가 더 크게 산출되어, 기준국의 지리적 분포가 URE 성능에 영향을 미친다는 사실을 확인할 수 있었다.
이번 장에서는 제안된 CNAV URA의 인덱싱 결과를 제시하고, 이를 LNAV URA와 비교 분석한다. 분석 과정에서 IGSO와 GEO 위성의 URA 결과가 유사한 경향을 보였기 때문에, WAD-RNSS 위성군에서 위성수가 더 많고 동적 궤도 특성을 갖는 IGSO 위성을 대표 사례로 선정하여 분석을 수행하였다. 또한, CNAV URA의 낮은 인덱스 구간에 대한 심층적 분석을 위해 모델링 오차의 표준편차는 1 m로 설정하였다. Fig. 6은 IGSO 위성의 URAED와 URANED 산출 결과를 보여준다. 좌측 그래프는 ED URA를, 우측 그래프는 NED URA를 나타낸다. 또한, 상단 그래프는 국내 기준국만 사용한 경우이며, 하단 그래프는 국내외 기준국을 모두 사용한 경우이다. 각 그래프의 오른쪽 축(분홍색 눈금)은 CNAV URA 인덱스를 나타내며, 인덱스 구간의 최대값에 해당 구간 인덱스를 표기하였다. 인덱스는 URAED와 URANED0에 적용된다. 예를 들어, 국내 기준국만 사용하는 경우, 예측 시간 12시간에서 URAED 인덱스는 5가 되며, URANED0 인덱스는 7이 된다. 반면, 국내외 기준국을 모두 사용하는 경우, 예측 시간 12시간에서 URAED 인덱스는 1이 되며, URANED0 인덱스는 4가 된다.
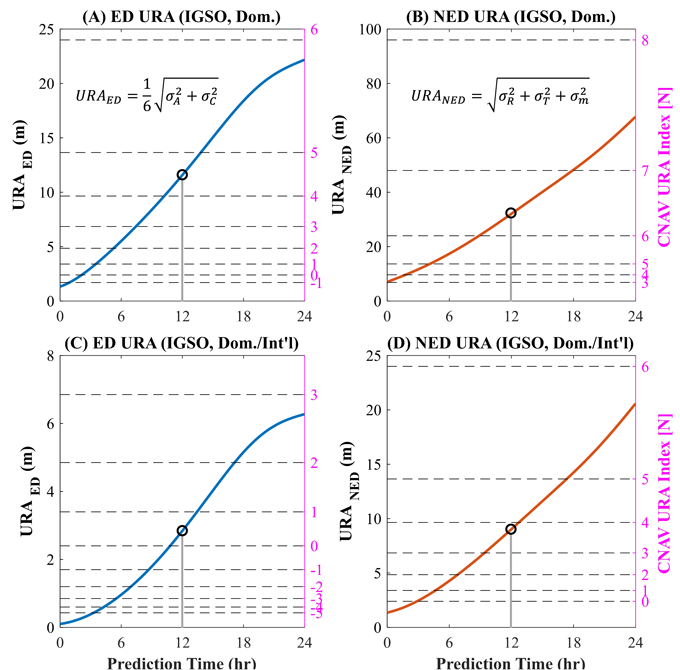
Fig. 6. URAED and URANED of IGSO satellite: Domestic-only (top) and domestic/international (bottom) reference ground stations.
Fig. 7은 예측 시간 경과에 따른 IGSO 위성의 LNAV 및 CNAV URA 변화를 나타낸다. 좌측 그래프는 국내 기준국만 사용한 시나리오를, 우측은 국내외 기준국 모두 사용한 시나리오의 결과를 각각 보여준다. 그래프에서 검정 실선은 식 (5)에 따라 산출된 URALNAV 값이다. 이는 고도각 0도일 때 URACNAV와 같으며, URACNAV의 최댓값에 해당한다. 그래프에서 LNAV URA와 CNAV URA는 각각 일점쇄선과 실선으로 나타냈다. 이번 분석에서는 4시간, 8시간, 16시간, 24시간의 URA 갱신 주기를 예시로 사용하였으며, 이를 그래프에서 서로 다른 색상으로 구분하여 도시하였다.
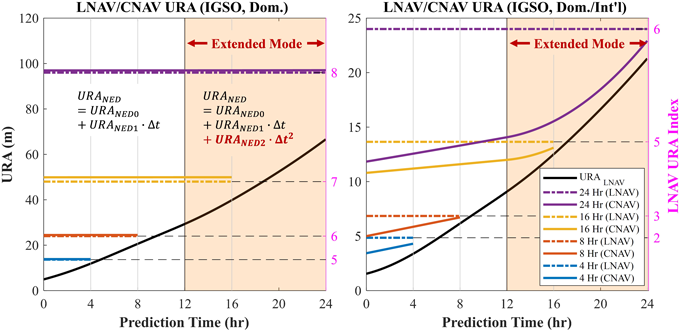
Fig. 7. LNAV and CNAV URA of ISGO satellite: Domestic-only (left) and domestic/international (right) reference ground stations.
이 연구에서 활용된 데이터셋은 24시간으로 제한되어 있어, GPS 표준에서 규정한 연장 운영 기준(26시간)을 그대로 적용하기 어려운 한계가 있었다. 이에 따라 연장 운영에 따른 성능 변화를 분석하기 위해 GPS 기준 대신 12시간을 대체 기준점으로 설정하여 분석을 수행하였다. 연장 운영 전에는 URANED는 1차항까지 적용되며, 연장 운영이 적용될 경우 2차항까지 포함한다. URANED의 1차 및 2차항을 나타내는 URANED1과 URANED2는 구간 인덱싱을 하지 않으며, 0과 7 사이에서 URANED를 가장 타이트하게 바운드하는 값으로 결정된다. Table 5에 예측 시간별 LNAV 및 CNAV URA 인덱스를 요약하였다.
Table 5. LNAV and CNAV URA indices across various prediction time.
| Message type | Index (N) | Prediction time (hr) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Domestic only | Domestic/International | ||||||||
| 4 | 8 | 16 | 24 | 4 | 8 | 16 | 24 | ||
| LNAV | URA | 5 | 6 | 7 | 8 | 2 | 3 | 5 | 6 |
| CNAV | URAED | 2 | 4 | 6 | 6 | −4 | −1 | 2 | 3 |
| URANED0 | 5 | 6 | 7 | 8 | 1 | 2 | 4 | 4 | |
| URANED1 | 7 | 7 | 7 | 7 | 0 | 1 | 1 | 0 | |
| URANED2 | N/A | 7 | 7 | N/A | 0 | 0 | |||
Fig. 7의 좌측 그래프를 보면, 국내 단독 기준국의 경우 CNAV URA가 LNAV URA보다 약간 크게 결정되는 현상이 관찰되었다. 다만, 그 차이가 최대 2 m 정도에 불과하여, 큰 오차 수준을 고려했을 때 두 값은 사실상 동일한 것으로 볼 수 있다. CNAV URA에서 지배적인 비중을 차지하는 것은 NED URA로, 오차 수준이 큰 환경에서는 CNAV의 URANED0와 LNAV URA가 동일한 인덱스 값을 갖게 된다. 이는 오차 규모가 URANED1과 URANED2의 표현 범위를 초과하여 이 두 항의 영향력이 제한되기 때문이다. 오히려 URANED0를 제외한 URANED1 , URANED2와 UREED에 따른 증가분으로 인해 CNAV URA가 LNAV URA보다 약간 크게 산출되는 결과가 나타났다.
반면, 오차 수준이 낮은 국내외 기준국 환경에서는 URA 변화량이 URANED1과 URANED2의 표현 범위 내에 포함되어, 이들 항을 통한 NED 오차 변화율의 효과적인 모델링이 가능해진다. 이로 인해 URANED0가 LNAV URA보다 작은 값으로 결정되며, 최종적으로 Fig. 7의 우측 그래프와 같이 CNAV URA가 LNAV URA보다 더 작게 산출되는 결과를 보인다. 또한, Table 5의 국내외 기준국 활용 시나리오 결과에서 볼 수 있듯이, CNAV URA는 초기 예측 구간에서 음수 인덱스를 활용함으로써 LNAV URA 인덱스보다 더 정밀한 예측 값을 제공한다.
본 연구 결과를 통해 CNAV URA는 URA 값이 작고 예측 시간에 따른 변화율이 낮은 조건에서 효과적으로 적용될 수 있음을 확인하였다. 이러한 조건을 만족시키기 위해서는 국내외 지상국 네트워크의 확보와 고성능 ODTS 알고리즘이 필요하다고 판단된다. 아울러 위성 궤도 및 시계 보정 정보의 정확도와 정밀도가 향상될 경우, CNAV URA의 장점을 보다 효과적으로 활용할 수 있을 것으로 기대된다.
본 연구에서는 한반도 지역 WAD-RNSS 환경에 적합한 CNAV URA 산출 모델을 새롭게 제안하고 검증하였다. 특히, 고도각에 영향을 받는 ED URA 파라미터와 영향을 받지 않는 NED URA 파라미터의 산출 방법을 제시하였다. 한국형 WAD-RNSS 시뮬레이션을 통해 생성된 위성 궤도 및 시계 오차의 예측 표준편차 데이터에 제안된 CNAV URA 결정 방법을 적용하였으며, WUL URE와 비교하여 산출된 URA가 보수적으로 WUL URE를 바운드하는 것을 확인하였다. 또한, 국내 기준국만 사용한 경우와 국내외 기준국을 모두 사용한 경우에 대해 24시간 예측 시간 동안의 CNAV URA를 산출하였고, 예측 시간에 따른 LNAV와 CNAV URA 인덱스를 비교 분석하였다. 분석 결과 CNAV URA 포맷 적용 시, LNAV에 비해 URA 값의 보수성을 완화할 수 있음을 확인하였다. 향후 연구에서는 장시간 데이터셋을 활용한 추가 분석과, cm급 URA 구현을 위한 CNAV 궤도 및 시계 보정 파라미터별 민감도 분석을 수행할 계획이다.
이 논문은 2023년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임 (UD230018TD).
Conceptualization, J. Kim and N. M. Kim; methodology, J. Kim and N. M. Kim; software, J. Kim and D. Kim; validation, N. M. Kim, D. Min, D. Kim, and J. Lee; formal analysis, J. Kim, N. M. Kim, and D. Min; investigation, J. Kim, N. M. Kim, and D. Min; resources, J. Kim, N. M. Kim, and D. Min; data curation, J. Kim and D. Kim; writing—original draft preparation, J. Kim, N. M. Kim, and D. Min; writing—review and editing, J. Kim, N. M. Kim, D. Min, and D. Kim; visualization, J. Kim and D. Kim; supervision, J. Lee; project administration, J. Lee; funding acquisition, J. Lee.
The authors declare no conflict of interest.
Ahn, H., Song, C., Yu, J., & Kim, T. 2020, A study on strategy of securing international resources for establishment of the Korean Positioning System, STEPI Final Report
GPS Official Website 2023, Civil Navigation (CNAV) Message [Internet] National Coordination Office for Space-Based Positioning, Navigation, and Timing, cited 2025 May 7, available from: https://www.gps.gov/systems/gps/modernization/cnav/
Heng, N., Gao, G., Walter, T., & Enge, P. 2012, GPS Signal-in-Space Integrity performance evolution in the last decade, IEEE Transactions on Aerospace and Electronic Systems, 48, 2932-2946. https://doi.org/10.1109/taes.2012.6324670
Joo, J. & Heo, M. 2020, Korean Positioning System development plan, in Proceedings 2020 IPNT Conference, Yeosu, Korea, 11-13 Nov 2020, pp.29-30. https://ipnt.or.kr/2020proc/110
Kim, D., So, H., & Park, J. 2021, Performance Analysis of Wide-Area Differential Positioning based on Regional Navigation Satellite System, Journal of Positioning Navigation and Timing, 10, 35-42. https://doi.org/10.11003/jpnt.2021.10.1.35
Kim, J., Kim, M., Min, D., Kim, D. & Lee, J. 2025, Analysis of User Range Accuracy in LNAV Message Format for WAD-RNSS, Journal of Positioning Navigation and Timing, 14, 53-62. https://doi.org/10.11003/JPNT.2025.14.1.53
Kim, K., Jo, Y., Park, B., & Kim, O. 2024, An Experimental Investigation on Broadcast Intervals and Sequences of GPS CNAV, QZSS LNAV/CNAV, and BDS CNAV/CNAV-2, Journal of Positioning Navigation and Timing, 13, 319-329. https://doi.org/10.11003/JPNT.2024.13.3.319
Lee, H., Kim, S., Park, J., Jeong, S., Park, S., et al. 2024, A Survey on New Parameters of GPS CNAV/CNAV-2 and Their Roles, Journal of Positioning Navigation and Timing, 13, 45-52. https://doi.org/10.11003/JPNT.2024.13.1.45
Navipedia 2011, GPS Navigation Message, Retrieved May 7, 2025, from https://gssc.esa.int/navipedia/index.php/GPS_Navigation_Message
Noh, J., Jo, G., Lee, J., & Lee, S. 2022, Performance Analysis of GNSS Navigation Messages in the Structure Viewpoint, Journal of Positioning Navigation and Timing, 11, 135-46. https://doi.org/10.11003/JPNT.2022.11.2.135
Park, J., Kim, B., Kee, C., & Kim, D. 2023, Performance Analysis of Real-time Orbit Determination and Prediction for Navigation Message of Regional Navigation Satellite System, Journal of Positioning, Navigation, and Timing, 12, 167-176. https://doi.org/10.11003/JPNT.2023.12.2.167
Rivers, M. H. 2000, The 2 SOPS User Range Accuracy (URA) improvement and Broadcast Inter-Frequency Bias (TGD) updates, Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2000), Sep 19-22, 2000, Salt Lake City, UT, pp.2551-2555. https://www.ion.org/publications/abstract.cfm?articleID=1681
U.S. Department of Defense 2020, Global Positioning System Standard Positioning Service Performance Standard, 5th, available from: https://www.gps.gov/technical/ps/
U.S. Department of Defense 2022a, Interface Control Documents, IS-GPS-200N, available from: https://www.gps.gov/technical/icwg/
U.S. Department of Defense 2022b, Interface Control Documents, IS-GPS-705J, available from: https://www.gps.gov/technical/icwg/