1Republic of Korea Air Force Academy, Cheongju 28187, Korea
2Department of Aerospace Engineering and the Institute of Advanced Machines and Design, Seoul National University, Seoul 08826, Korea
3Republic of Korea Army College, Daejeon 34059, Korea
†Corresponding Author: Changdon Kee, E-mail: kee@snu.ac.kr
Citation: Kang, M., Jeong, H., Park, J., Song, J., & Kee, C. 2025, Design of Navigation Satellite Constellation for Lunar South Pole PNT, Journal of Positioning, Navigation, and Timing, 14, 131-138.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 June, Volume 14, Issue 2, pages 131-138. https://doi.org/10.11003/JPNT.2025.14.2.131
Received on May 12, 2025, Revised on May 24, 2025, Accepted on May 29, 2025, Published on Jun 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
The Lunar Navigation Satellite System (LNSS) is designed to provide precise positioning information to users on the lunar surface, similar to the Global Navigation Satellite System (GNSS) on Earth. However, various perturbative forces can cause the orbits of lunar navigation satellites to change over time, degrading navigation performance. Given the high cost of lunar orbit insertion, maintaining stable orbits is critically important. This paper presents the design of satellite orbits that offer longterm, reliable navigation services at the lunar south pole. To maintain orbital stability, we analytically derived the conditions for lunar frozen orbits, considering the dominant perturbative influence of Earth’s three-body gravity using the Lagrange planetary equations. Additionally, we analyzed the stability changes of Frozen orbits when additional perturbative forces due to the Moon’s oblateness are considered, specifically incorporating the J2 term. Among the candidate stable frozen orbits that account for both Earth’s three-body gravity and lunar perturbations, we selected the optimal orbits based on their superior navigation performance, which was evaluated using the Dilution of Precision (DOP) metric. The long-term navigation performance at the lunar south pole was then verified through orbital propagation simulations.
lunar navigation satellite system, frozen orbit, ELFO, dilution of precision
달은 차세대 우주거점으로서 국제사회의 전략적 관심이 집중되고 있으며 NASA, ESA, JAXA 및 KASA 등 주요 우주기관들이 다양한 달 탐사 임무를 추진 중이다. 이러한 임무를 안정적으로 수행하기 위해서는 달에서도 정확한 위치정보를 제공할 수 있는 항법 시스템의 구축이 필수적이다. 현재 달에는 항법 인프라가 존재하지 않기 때문에 지구 기반의 통신 네트워크에 의존하거나 또는 탐사선 탑재 센서를 이용하여 제한적으로 위치를 추정하고 있으며 대표적으로 Terrain Relative Navigation (TRN), Deep Space Network (DSN), 지구 Global Navigation Satellite System (GNSS) 방식이 있다. TRN은 실시간으로 획득한 영상과 사전에 확보된 고해상도 지형 데이터를 비교하여 위치를 추정하는 기법으로, 항법 신호가 도달하지 않는 지역에서도 활용 가능하다는 장점이 있다. 그러나 어두운 지역이나 음영 지형처럼 시각적 정보가 제한된 환경에서는 정확도가 저하되며, 고성능 센서와 복잡한 영상 처리 연산이 필요하다는 점에서 실시간 처리에 한계가 존재한다 (Johnson & Montgomery 2008). DSN은 지구의 대형 안테나 네트워크를 활용하여 양방향 통신을 통해 탐사선의 위치를 추적할 수 있다. 그러나 심우주 임무의 수요 증가로 인해 DSN 채널의 가용성이 제한되고 있으며, 특히 달 뒷면처럼 지구와 가시선이 확보되지 않는 지역에서는 신호 수신이 불가능하다. 또한 지구와 달 간 거리로 인한 신호 지연은 실시간 항법 정보 제공에 불리하게 작용한다. GNSS 신호는 원래 지구 기반 사용자를 위해 설계된 것이기 때문에 달까지 도달하는 신호는 매우 약하고, 제한적인 각도에서만 수신이 가능하다. NASA의 Magnetospheric Multiscale (MMS) 임무를 통해 지구에서 약 18만 km 거리까지는 신호 수신이 가능함이 입증되었지만 (Winternitz et al. 2017), 달 표면 전역을 안정적으로 커버하기에는 신호 세기, 위성의 기하학적 배치, 가시성 측면에서 여전히 많은 제약이 존재한다.
달 궤도 기반의 위성 항법시스템인 Lunar Navigation Satellite System (LNSS)은 이러한 기존 항법 방식들의 한계를 극복하고 달에서 독립적이고 안정적인 PNT 서비스를 제공하기 위한 항법 방식이다. LNSS는 지구와의 시각 동기화를 수행하는 주 위성과 항법 신호를 방송하는 복수의 초소형급 항법 위성으로 구성되며, 달 궤도 상에 위성을 배치하여 달 사용자에게 안정적인 위치정보를 제공한다. 이는 달 탐사 단계에 따라 항법 서비스 지역을 점진적으로 확장하는 방안이 제안되고 있다. 달 남극 지역에는 충돌 크레이터 내부에 위치한 영구 음영 지역 (permanently shadowed region)이 다수 분포하고 있으며, 이들 지역은 극저온 환경 특성으로 인해 얼음 형태로 물이 존재할 가능성이 높은 곳으로 평가되고 있다. 또한 크레이터의 가장자리 (crater rims) 지역은 일정한 일조 조건을 갖추고 있어 태양광을 활용한 전력 생산에 유리한 환경을 제공한다 (Speyerer & Robinson 2013). 이러한 조건은 장기 유인 탐사 및 기지 건설에 필수적인 물과 에너지원 확보 측면에서 전략적 이점을 가지며, 이에 따라 남극점은 달 탐사의 초기 거점으로서 높은 우선순위를 지닌다. 따라서 달 위성 항법시스템은 2020년대 후반까지 달 남극점 지역을 중심으로 항법 서비스를 우선적으로 제공하고, 이후 2030년대에 달 전역으로 항법 커버리지를 확대하는 단계적인 구상 (NASA & ESA 2022)이 계획되고 있으며, 이를 위한 항법위성 궤도군 설계가 다수 선행연구에서 제안되었다 (Israel et al. 2020, Pereira & Selva 2020, Giordano et al. 2022, Murata et al. 2022, 2024).
LNSS 항법 위성의 궤도는 궤도가 크게 변하지 않는 안정한 궤도로 설계되어야 한다. 달 궤도는 지구보다 불균일한 달의 중력장과 삼체 중력 등 다양한 섭동 (perturbation) 요인의 영향을 받아 위성 궤도가 시간에 따라 변화하게 된다. Fig. 1은 지구 궤도 (Urrutxua & Lara 2016)와 달 궤도에서 고도별로 궤도에 작용하는 힘을 나타낸 것으로, 지구와 달리 달에서는 삼체 중력 (third body)인 지구의 섭동영향이 우세하다. 궤도의 안정성이 높을수록 섭동 환경 속에서도 궤도 수정을 위한 연료 소모를 최소화하여 위성 수명을 연장할 수 있으며, 항법 메시지 생성을 위한 방송 궤도력 생성에도 유리하다. 또한, 사용자에게 제공되는 위치 정확도는 항법 위성들의 기하학적 배치에 따라 결정되므로, 궤도 안정성과 함께 양호하게 배치되도록 궤도군을 설계해야 한다. 이와 같은 궤도 안정성과 항법 성능은 LNSS 궤도군 설계에 있어 핵심 요소이다.
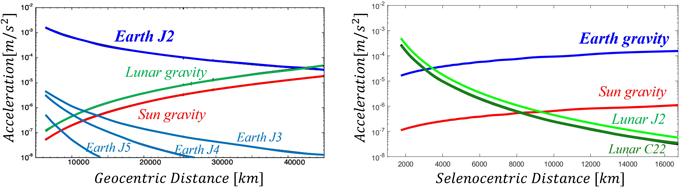
Fig. 1. Perturbation environment in Earth orbit (left) and Lunar orbit (right).
본 연구에서는 LNSS의 초기 단계에서 위성 수를 최소화하면서도 달 남극점 지역에서 요구되는 항법 성능과 궤도 안정성을 동시에 만족할 수 있는 항법 위성 궤도군을 설계하였다. 장기적으로 안정적인 궤도 요소를 유지할 수 있도록 Elliptical Lunar Frozen Orbit (ELFO)를 기반으로 궤도군을 구성하였으며, 서울대학교 GNSS 연구실에서 개발한 달 궤도 설계 시뮬레이션 툴 (Jeong et al. 2023)을 활용하여 설계하고 상용 GMAT 프로그램으로 이를 검증하였다.
달 궤도를 설계하기 위해서는, 지구와는 상이한 달의 기하학적 특성을 반영한 좌표계 정의가 선행되어야 한다. 달은 지구로부터 약 384,400 km 떨어진 궤도를 공전하며, 약 27.3일의 공전 주기를 가진다. 조석 고정 (tidal locking)의 영향으로 인해, 자전주기와 공전 주기가 일치하며, 이로 인해 항상 동일한 반구가 지구를 향하게 된다. 달의 공전면은 태양을 중심으로 도는 지구의 공전 궤도면인 황도면 (ecliptic)에 대해 약 5.14° 기울어져 있으며, 달의 적도면은 달의 공전면에 대해 약 6.7°의 경사각을 지닌다. 이러한 궤도면의 기하학적 관계를 바탕으로, 다양한 달 좌표계를 정의할 수 있다.
달 중심 관성 좌표계 (Moon-Centered Inertial, MCI)는 지구 중심 관성 좌표계 (Earth-Centered Inertial, ECI)의 원점을 달 중심으로 평행 이동하여 정의되며, 기준면은 ECI 좌표계와 동일하게 지구 적도면이다. X축은 지구 시 (Terrestrial time) 기준 2000년 1월 1일 12시 (J2000)의 춘분점 (vernal equinox)을 향하고, Z축은 해당 시점에서의 지구 자전축 방향과 일치하며, Y축은 오른손 법칙에 따라 정의된다. MCI는 달의 자전 운동과 무관한 관성 좌표계로 간주되며, 궤도 전파를 위한 수치적분에 사용된다.
달 중심 고정 좌표계 (Moon-Centered Moon-Fixed, MCMF)는 달의 중심을 원점으로 하며 달의 적도면을 기준면으로 하는 비관성 좌표계이다. 이 달 적도 좌표계는 크게 Principal Axis (PA) 좌표계와 Mean Earth / Polar axis (ME) 좌표계로 나눌 수 있다. PA 좌표계는 달의 질량 중심을 기준으로 한 주축 (principal axes)으로 정의되며, 주로 달의 물리적 특성 분석이나 중력장 모델링 등에 활용된다. 반면, ME 좌표계는 달 탐사에서 표준 좌표계로 널리 사용되며, X축은 달 중심에서 평균적으로 지구를 바라보는 방향 (본초 자오선)으로 정의되며, Z축은 평균 자전축과 일치하며, Y축은 오른손 법칙에 따라 정의된다 (GSFC 2008). 달의 비대칭 질량 분포로 인해 PA 좌표계와 ME 좌표계는 달 표면에서 약 1 km의 위치 차이를 보인다. 본 연구에서는 ME 기반 MCMF 좌표계를 사용하여 달 표면 사용자 기준의 항법성능 분석에 적용하였다. MCMF 좌표계는 PA 좌표계로의 변환과 달 적도면 기준의 PA 좌표계를 지구 적도면 기준 좌표계로 변환함으로써 MCI 좌표계로 변환할 수 있다. ME와 PA 좌표계 사이의 변환은 Eq. (1)과 같이 고정 상수에 대한 회전 변환 행렬 (C)을 통해 계산할 수 있다. 고정된 상수 ($C_1$, $C_2$, $C_3$)는 NASA의 Jet Propulsion Laboratory에서 제공하는 천체 궤도력에서 정의된 ME와 PA 사이 각으로서 Table 1과 같다 (Ye et al. 2018). 본 연구에서는 천체 궤도력으로 DE421을 사용하였다.
$$\begin{align}
\mathbf{C} &= R_z(C_1) R_y(C_2) R_x(C_3) \notag \\
&=
\begin{bmatrix}
\cos C_1 & \sin C_1 & 0 \\
-\sin C_1 & \cos C_1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos C_2 & 0 & -\sin C_2 \\
0 & 1 & 0 \\
\sin C_2 & 0 & \cos C_2
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos C_3 & \sin C_3 \\
0 & -\sin C_3 & \cos C_3
\end{bmatrix} \notag \\
\vec{r}_{PA} &= \mathbf{C} \cdot \vec{r}_{ME}
\end{align}$$
Table 1. Transition angles between two MCMF frame (ME and PA).
| C1 | C2 | C3 | |
|---|---|---|---|
| DE421 | 67.92″ | 78.56″ | 0.30″ |
특정 시점에서 지구에 대한 달의 방향 (orientation)은 천체 궤도력으로부터 오일러 각 ($\phi_m$, $\theta_m$, $\psi_m$)으로 정의되며 이를 이용하여 Eq. (2)와 같이 변환행렬 (L)을 통해 PA 좌표계를 지구 적도면 기준의 MCI 좌표계로 변환할 수 있다 (Taylor et al. 2010).
$$\begin{align}
\mathbf{L} &= R_z(-\phi_m) R_y(-\theta_m) R_x(\psi_m) \notag \\
&=
\begin{bmatrix}
\cos \phi_m & -\sin \phi_m & 0 \\
\sin \phi_m & \cos \phi_m & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos \theta_m & 0 & \sin \theta_m \\
0 & 1 & 0 \\
-\sin \theta_m & 0 & \cos \theta_m
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos \psi_m & -\sin \psi_m \\
0 & \sin \psi_m & \cos \psi_m
\end{bmatrix} \notag \\
\vec{r}_{MCI} &= \mathbf{L} \cdot \vec{r}_{PA}
\end{align}$$
지구 궤도 좌표계 (Earth Orbit Frame, EOF)는 원점이 달 중심이며 지구를 도는 달의 공전 궤도면을 기본평면으로 하는 좌표계로서, 가장 우세한 섭동요인인 지구 중력의 영향을 분석하는 데 사용된다 (Ely 2005). 달의 공전 궤도면과 EOF 좌표계의 각 축은 Fig. 2와 같이 특정 시점에 MCMF 좌표계에서 정의된 지구의 위치 벡터 $\vec{r}_{earth}$와 속도 벡터 $\vec{v}_{earth}$를 이용하여 계산할 수 있다. Z축은 공전면의 각운동량 벡터 방향이며 이는 $\vec{r}_{earth}$과 $\vec{v}_{earth}$의 외적으로 계산된다. X축은 달의 적도면과 궤도면의 교차 방향을 가리키며, 이는 달 자전축 벡터와 Z축의 외적을 통해 계산된다. Y축은 오른손 법칙에 따라 정의된다.
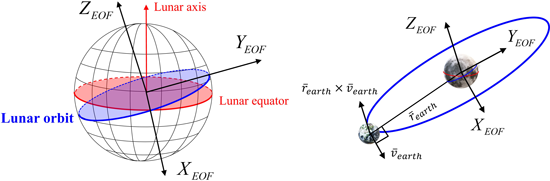
Fig. 2. Axes of Earth orbit frame.
$$\begin{bmatrix}
x_{EOF} \\
y_{EOF} \\
z_{EOF}
\end{bmatrix}
=
[\mathbf{R}]
\begin{bmatrix}
x_{MCMF} \\
y_{MCMF} \\
z_{MCMF}
\end{bmatrix}, \quad
[\mathbf{R}] =
\begin{bmatrix}
\frac{[0,0,1] \times \vec{Z}_{EOF}}{|[0,0,1] \times \vec{Z}_{EOF}|} \\
\frac{\vec{Z}_{EOF} \times \vec{X}_{EOF}}{|\vec{Z}_{EOF} \times \vec{X}_{EOF}|} \\
\frac{\vec{r}_{earth/MCMF} \times \vec{v}_{earth/MCMF}}{|\vec{r}_{earth/MCMF} \times \vec{v}_{earth/MCMF}|}
\end{bmatrix}$$
EOF 좌표계는 매 시점의 MCMF 좌표계에서 정의된 지구의 위치 및 속도 벡터를 기준으로 구성되기 때문에 시간에 따라 기준면이 변화한다. 하지만 궤도면의 각운동량 벡터는 거의 일정하게 유지되며, 공전 궤도면이 달 적도면에 대해 이루는 경사각 또한 20년 동안 ±0.2 degree 이내의 미세한 범위에서만 변동한다 (Fig. 3). 따라서 EOF 좌표계는 준 관성계 (quasi-inertial frame)로 간주할 수 있으며, 지구 중력 영향 하에서 위성 궤도의 변화를 분석하거나 안정한 궤도를 설계하기 위한 기준 좌표계로 사용된다.
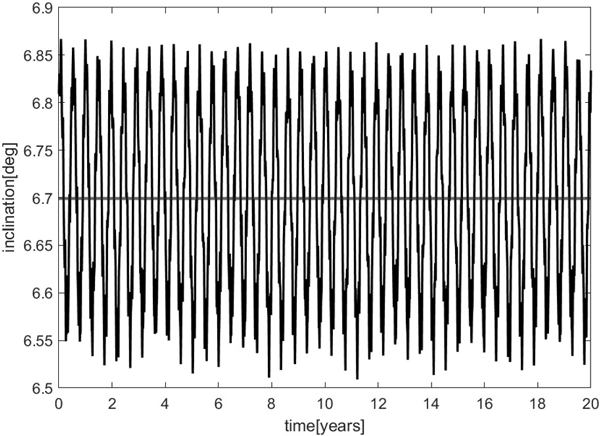
Fig. 3. 20 years orbital inclination relative to the lunar equator.
본 연구는 장기간 항법성능을 유지하기 위해 안정한 달 Frozen orbit으로 궤도군을 설계하였다. Frozen orbit은 궤도요소의 변화가 최소인 안정한 궤도를 의미하며 이를 설계하기 위해서는 궤도에 작용하는 섭동영향을 고려해야 한다. 본 연구에서는 달 궤도에서 가장 우세한 지구 중력의 영향을 최소화하는 궤도 조건으로 설계하였다. 지구 섭동력에 의한 궤도요소의 변화율은 라그랑주 행성방정식 (Lagrange Planetary equations)과 지구 삼체중력의 섭동함수 (Folta & Quinn 2006)로부터 Eq. (4)와 같이 해석적으로 유도된다 (Ely 2005). a, e, i, Ω, ω, M0는 케플러 궤도요소 6가지를 의미하며 n과 nE는 각각 위성의 mean motion과 달에 대한 지구의 mean motion을 의미한다. 각 변화율은 궤도요소의 선형적인 영년 변화 (secular drift)를 의미 (Vallado 2013)하며 EOF 좌표계에서 정의된다.
$$\begin{align}
\frac{da}{dt} &= 0 \notag \\
\frac{de}{dt} &= \frac{15 n_E^2}{8n} e \sqrt{1 – e^2} \sin^2 i \sin 2\omega \notag \\
\frac{di}{dt} &= -\frac{15 n_E^2 e^2}{16 n \sqrt{1 – e^2}} \sin 2i \sin 2\omega \notag \\
\frac{d\Omega}{dt} &= \frac{3 n_E^2 \cos i}{8 n \sqrt{1 – e^2}} \left( 5e^2 \cos 2\omega – 3e^2 – 2 \right) \notag \\
\frac{d\omega}{dt} &= \frac{3 n_E^2}{8 n \sqrt{1 – e^2}} \left[ (5 \cos^2 i – 1 + e^2) + 5(1 – e^2 – \cos^2 i) \cos 2\omega \right] \notag \\
\frac{dM_0}{dt} &= -\frac{n_E^2}{8n} \left[ (3e^2 + 7)(3\cos^2 i – 1) + 15(1 + e^2) \sin^2 i \cos^2 \omega \right]
\end{align}$$
Frozen orbit은 2개 이상의 궤도요소의 영년 변화가 최소인 궤도로서 주기적인 변화만 나타나며 궤도형태와 경사각 및 근월점 (perilune)의 방향이 일정하게 유지된다.
$$\frac{da}{dt} = \frac{de}{dt} = \frac{di}{dt} = \frac{d\omega}{dt} = 0$$
Eqs. (4, 5)로부터 지구 중력의 영향에도 궤도가 안정한 달 Frozen orbit의 설계 조건은 Eqs. (6, 7)과 같이 도출된다 (Ely 2005).
$$e = \sqrt{1 – \frac{5}{3} \cos^2(i)}$$
$$\omega = 90^\circ, \; 270^\circ$$
남극점을 커버하는 LNSS 1단계에서는 항법위성이 남반부에서 오랫동안 체공하도록 궤도를 설계해야 하기 때문에 ω=90°로 설계한다. 이러한 달 Frozen orbit은 타원형태의 Elliptical Lunar Frozen Orbit (ELFO)가 되며 달과 가까운 근월점에서는 달 섭동력의 영향을 크게 받게 된다. 본 연구에서는 근월점 (rp)에서의 궤도 변화로 인한 달 표면과의 충돌을 방지하기 위해 최소고도 (hmin)를 300 km로 설계하였으며 Eq. (8)의 trajectory equation에 따라 장반경 a는 Eq. (9)와 같이 이심률 e값에 따라 결정된다 (Song 2024).
$$r = \frac{a(1 – e^2)}{1 + e \cos \nu}$$
$$a = \frac{r_p}{1 – e} = \frac{R_m + h_{\min}}{1 – e} = \frac{(R_m + 300)}{1 – e} [\text{km}]$$
한편, 궤도군은 사용자에게 일관된 가시위성 수를 보장하기 위해, 두 개 이상의 궤도면으로 구성되며, 각 궤도면은 Ω이 균등한 간격으로 배치되도록 설계된다. 또한 동일한 궤도면에 속한 위성들은 사용자 기준에서 동일한 비행시간 간격을 유지해야 하므로, 균등한 평균 근점이각(M) 간격으로 배치되어야 한다.
$$\Delta \Omega = \frac{360^\circ}{n_{orbit}}, \quad \Delta M = \frac{360^\circ}{n_{sat\_orbit}}$$
남극점을 커버하는 Frozen orbit 설계 조건은 Eqs. (6-10) 구속조건으로부터 경사각 에 따라 결정되며, 이로 인해 가능한 궤도군의 조합은 무수히 많이 존재한다. 따라서 이들 중에서 항법 성능이 우수한 궤도군 조건을 선별하는 것이 필요하다. 위성 항법시스템의 항법성능은 위성들의 기하학적 배치에 크게 의존 (Kaplan & Hegarty 2006)하므로, 동일한 Frozen orbit이라 하더라도 사용자 기준에서 가시위성의 배치가 양호한 궤도군을 선택하는 것이 중요하다. 항법위성 궤도군이 사용자에게 위치정보를 제공하기 위해서는 필수적으로 사용자 기준에서 항상 최소 4기 이상 가시위성이 확보되어야 한다. Song (2024)에서 mask angle 5 degree를 기준으로 분석한 결과, 위성 수가 6기 이하일 경우 일부 epoch에서 가시위성 수가 4기 미만으로 떨어지는 구간이 발생하여, 본 연구에서는 총 8기의 위성을 2개의 궤도면에 균등하게 배치하였다. 궤도면 간 Ω는 EOF 좌표계 기준으로 180 degree 간격으로 배치하며, 각 궤도면 내 위성은 90 degree의 균등한 M 간격으로 배치하였다. 이 때, 동일한 궤도면에 배치되는 위성들은 동등한 궤도 에너지를 가지나 섭동력의 영향을 받으면 위성별로 궤도 에너지의 수준이 달라진다. 이로 인해 Fig. 4에서 나타나듯 위성별 평균 장반경의 차이가 발생하며 시간에 따라 위성 간 간격이 변화하여 초기 설계된 항법성능이 악화된다 (Ely & Lieb 2006). 본 연구에서는 iteration을 통해 Fig. 5와 같이 위성별로 달의 자전주기 (27.3일) 동안 평균 장반경의 차이가 0.01 km 이내가 되도록 초기 장반경 값을 조절하여 설계하였다.
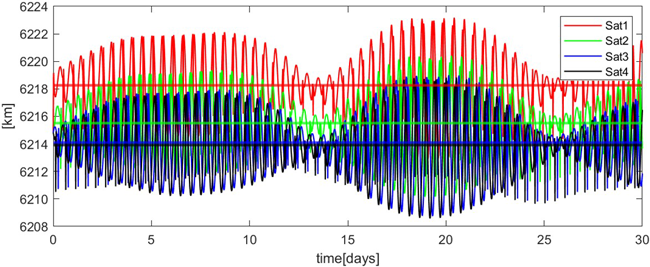
Fig. 4. Variation in semi-major axis of coplanar satellites (uniform initial value).
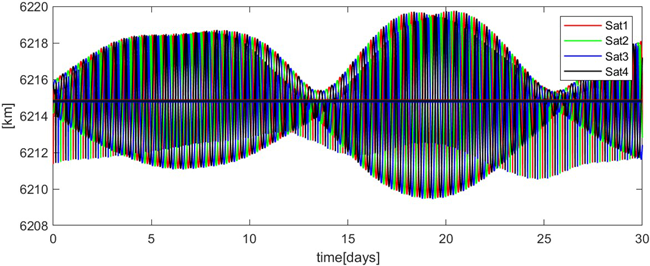
Fig. 5. Variation in semi-major axis of coplanar satellites (modified initial value).
결국 달 Frozen orbit으로 이루어진 항법위성 궤도군은 궤도 형태를 결정하는 경사각 i와 두 궤도면 간 위성 배치의 위상 차인 ΔM0 (Fig. 6)에 따라서 각기 다른 궤도군으로 설계될 수 있다. 궤도면 간 위상 차는 위성들의 기하학적 배치에 영향을 미치며, 이는 곧 항법성능의 차이를 유발하게 된다. 본 연구에서는 Eq. (6)의 해 중 남극점 사용자 기준 가시성 조건과 달의 섭동 환경을 고려한 궤도 안정성 조건 (Elipe & Lara 2003)을 함께 만족하는 44 ~ 57 degree 구간을 경사각 분석 범위로 설정하였다 (Song 2024). ΔM0는 두 궤도면 간 상대 위상을 조절하는 변수로, -45 ~ 45 degree 범위 내에서 변화시키며 항법성능을 분석하였다. 항법성능은 남극점 고정 사용자를 기준으로 한 Horizontal Dilution of Precision (HDOP) 값을 통해 평가하였으며 mask angle은 5 degree, 성능 기준 임계값은 HDOP ≤ 3.5로 설정하였다. 따라서 본 연구의 목적은 경사각 i와 위상 차 ΔM0 조건에 따라 구성된 다양한 궤도군 중에서 남극점 기준 가장 HDOP 값이 낮은 조건을 도출하는 데 있다.
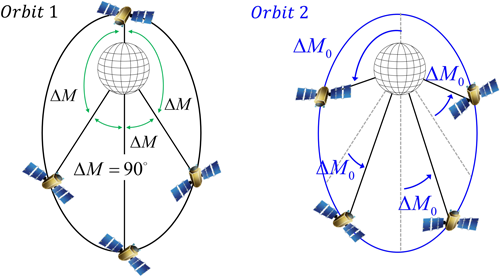
Fig. 6. Satellite deployment for each orbital planes (ΔM0).
본 연구에서는 해석적으로 지구 중력의 영향을 최소화하도록 설계된 달 Frozen orbit이 장기적으로 궤도요소의 안정성을 유지할 수 있는지를 검증하였다. 또한, 해당 궤도가 지구 중력 외의 추가적인 섭동력이 포함된 실제 달 궤도 환경에서도 안정성을 유지하는지를 함께 분석하였다. 궤도 전파 (orbit propagation)는 서울대학교 GNSS 연구실에서 개발한 LNSS 궤도 시뮬레이션과 상용 GMAT 프로그램을 활용하였으며, 적용된 시뮬레이션 설정은 Table 2와 같다.
Table 2. Stability analysis setting.
| Setting | Value |
|---|---|
| Tool | SNU LNSS simulation tool |
| Method | Runge-Kutta 4th |
| Interval | 300 sec |
| Period | 20 years |
| Ephemeris | DE 421 |
| Perturbation | Earth gravity + Lunar J2 |
Fig. 7은 Table 3의 임의의 Frozen orbit에 대해 지구 중력만 반영한 경우와 지구 중력 외 우세한 달의 J2 섭동력까지 반영하여 주요 궤도요소의 변화를 나타낸 것이다. 분석 결과에서 알 수 있듯, 지구 중력만을 고려하여 Frozen orbit을 설계하더라도 복합적인 섭동력이 작용하는 환경에서 20년 이상의 기간 동안 궤도 요소의 안정성이 유지됨을 확인하였다. 이를 통해 해석적으로 도출된 Frozen orbit 설계 조건이 실제 운용 환경에서도 유효함을 검증할 수 있었다.
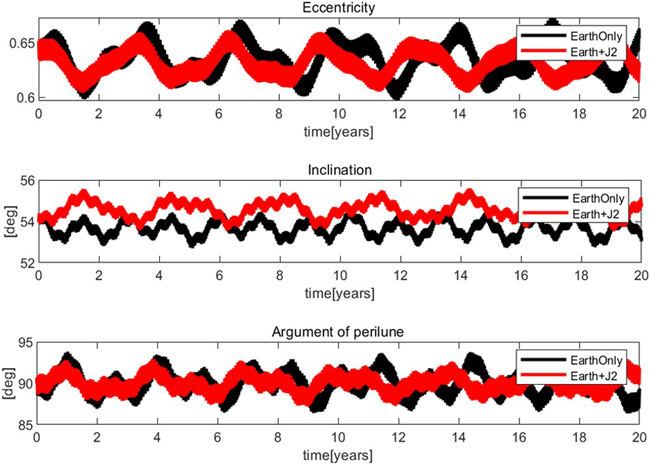
Fig. 7. Orbital variations of frozen orbit (Earth vs Earth+J2).
Table 3. Initial Keplerian orbit elements of arbitrary Lunar frozen orbit.
| a (km) | e | i (°) | Ω (°) | ω (°) | M0 (°) |
|---|---|---|---|---|---|
| 5844.0 | 0.65 | 54.0 | 0.0 | 90.0 | 0.0 |
항법성능 분석은 경사각 i와 궤도면 간 위상차 ΔM0의 조합에 따라 구성된 궤도군 별 남극점 기준으로 계산한 Root Mean Square (RMS) HDOP을 지표로 사용하였다. 각 궤도군에 대해 지구 섭동력만 반영하여 500일 간 60초 간격으로 전 epoch HDOP 값을 산출하고 대푯값으로서 RMS HDOP를 비교하였다. 분석 결과는 i–ΔM0 조건별로 2차원의 contour plot 형태로 시각화하여 Fig. 8에 제시하였다. 파란색일수록 HDOP가 낮아 항법성능이 우수하며 빨간색일수록 성능이 열악한 조건을 나타낸다. 경사각이 낮은 경우 궤도의 이심률과 장반경이 작아져 남극점 체류 시간이 짧아져 HDOP가 증가하는 경향을 보였으며, 반면 경사각이 증가함에 따라 전반적으로 항법 성능이 개선되는 것으로 나타났다. 특히, 경사각이 54 degree 이상인 구간에서는 두 궤도면에 위성을 대칭적으로 배치 (ΔM0 = 0°)할 수록 항법성능이 우수한 경향을 보였으며, 위상차가 커질수록 성능 저하가 관측되었다. 최적의 항법 성능은 i = 55°, ΔM0 = 0° 조합에서 나타났으며, 이 조건에서의 RMS HDOP는 1.25로 계산되었다.
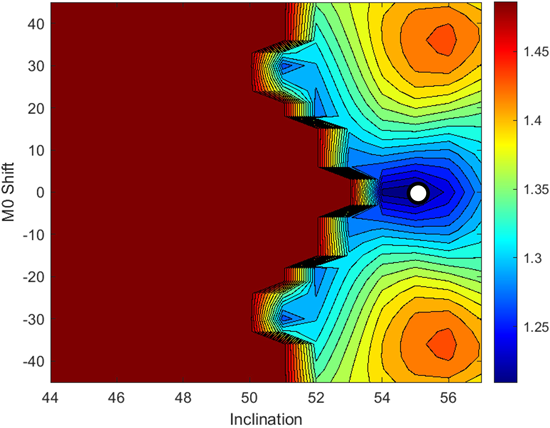
Fig. 8. HDOP analysis result (500 days).
항법성능 분석을 통해 설계된 남극점을 커버하는 궤도군에 대해, 보다 현실적인 달 궤도 환경을 반영하여 장기간 항법 성능을 검증하였다. 이를 위해 달 섭동력 고차항과 태양 삼체 중력 및 태양 복사압까지 포함하였으며, NASA의 상용 궤도 전파 프로그램 GMAT을 활용하였다. 남극점 단일 지점의 HDOP를 5년간 검증하였으며, 상세 설정은 Table 4에 제시되어 있다. 설계 궤도군의 형태 및 위성별 세부 궤도요소는 Fig. 9와 Table 5와 같다. 검증 결과 (Fig. 10), 궤도 수정 없이도 5년 간 남극점에서 요구 항법성능을 만족하며 RMS HDOP 1.29, Max HDOP 2.44로 안정적인 항법 서비스를 제공할 수 있음을 확인하였다.
Table 4. Verification settings.
| Tool | NASA GMAT software | Ephemeris | DE 421 |
|---|---|---|---|
| Method | Runge-Kutta 68 | Perturbation | Earth, Sun |
| Time | 60 sec / 5 years | GRGM 900C (degree:12 / order: 12) Solar radiation pressure (Spherical model) |
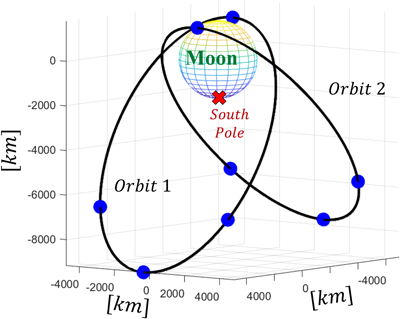
Fig. 9. Configuration of designed constellation.
Table 5. Keplerian orbit elements of designed constellation.
| a (km) | e | i (°) | Ω (°) | ω (°) | M0 (°) |
|---|---|---|---|---|---|
| 6,211.40 | 0.67 | 55 | 0 | 90 | 0 |
| 6,214.13 | 0.67 | 55 | 0 | 90 | 90 |
| 6,215.52 | 0.67 | 55 | 0 | 90 | 180 |
| 6,215.73 | 0.67 | 55 | 0 | 90 | 270 |
| 6,215.35 | 0.67 | 55 | 180 | 90 | 0 |
| 6,213.94 | 0.67 | 55 | 180 | 90 | 90 |
| 6,215.39 | 0.67 | 55 | 180 | 90 | 180 |
| 6,215.49 | 0.67 | 55 | 180 | 90 | 270 |
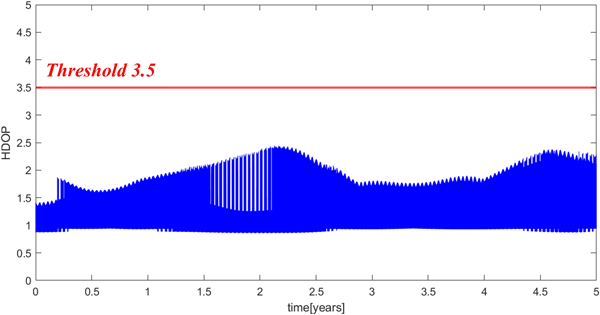
Fig. 10. Verification result of HDOP at the south pole (GMAT).
본 연구에서는 달 남극점 지역에서의 항법 서비스를 제공하기 위한 LNSS 항법위성 궤도군 설계 방안을 제시하였다. 장기간 안정적인 운용을 목표로, 해석적으로 도출된 Frozen orbit 조건을 기반으로 궤도를 구성하고, 다양한 섭동 환경을 반영한 수치적 시뮬레이션을 통해 궤도 안정성을 검증하였다. 분석 결과, 지구 중력만을 고려한 Frozen orbit 조건이 복합 섭동 환경에서도 장기간 궤도의 안정성을 유지함을 확인하였다.
항법 성능 측면에서는 궤도 경사각 i와 궤도면 간 위성 배치의 위상 차 ΔM0에 따른 HDOP 성능을 분석하였다. 그 결과, 총 8기의 위성을 경사각 55 degree의 2개 궤도면에 대칭적으로 배치할때 가장 우수한 HDOP 성능이 도출되었다. 또한, 설계된 위성군에 대해 GMAT 상용 프로그램을 활용하여 복잡한 섭동환경 하에서 5년 간 남극점 고정 사용자를 기준으로 항법성능을 검증한 결과, 궤도 수정 없이도 요구조건을 만족하는 항법 서비스를 제공할 수 있음을 확인하였다.
본 연구는 LNSS 연구의 1단계로서, 달 남극점 지역을 효율적이고 안정적으로 커버할 수 있는 항법위성 궤도군 설계 기준을 제시하였으며, 향후 달 전역으로 항법 커버리지를 확장하기 위한 설계의 기반이 될 수 있을 것으로 기대된다.
This research was supported by Unmanned Vehicles Core Technology Research and development Program through the National Research Foundation of Korea (NRF), Unmanned Vehicle Advanced Research Center (UVARC) funded by the Ministry of Science and ICT, the Republic of Korea, contracted through by SNU Future Innovation Institute (No. 2020M3C1C1A01086407). And this work was supported by Future Space Navigation & Satellite Research Center through the National Research Foundation funded by the Ministry of Science and ICT, the Republic of Korea (2022M1A3C2074404). This research was supported (in part) by the Institute of Advanced Aerospace Technology at Seoul National University. The Institute of Engineering Research at Seoul National University provided research facilities for this work.
Conceptualization, M.K.; methodology, J.S., M.K., and H.J.; software, J.P., J.S., and M.K.; validation, M.K., H.J., and J.P.; formal analysis, M.K. and H.J.; investigation, J.P., H.J., J.S., and M.K.; resources, M.K., H.J., and J.P.; data curation, M.K., J.S., and H.J.; writing—original draft preparation, M.K.; writing—review and editing, M.K.; visualization, M.K.; supervision, C.K.
The authors declare no conflict of interest.
Elipe, A. & Lara, M. 2003, Frozen orbits about the Moon, Journal of Guidance, Control, and Dynamics, 26, 238243. https://doi.org/10.2514/2.5064
Ely, T. A. 2005, Stable constellations of frozen elliptical inclined lunar orbits, The Journal of the Astronautical Sciences, 53, 301-316. https://doi.org/10.1007/BF03546355
Ely, T. A. & Lieb, E. 2006, Constellations of elliptical inclined lunar orbits providing polar and global coverage, The Journal of the Astronautical Sciences, 54, 53-67. https://doi.org/10.1007/BF03256476
Folta, D. & Quinn, D. 2006, Lunar frozen orbits, AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21-24 August 2006, pp.1-18. https://doi.org/10.2514/6.2006-6749
Giordano, P., Malman, F., Swinden, R., Zoccarato, P., & Ventura-Traveset, J. 2022, The Lunar Pathfinder PNT Experiment and Moonlight Navigation Service: The future of lunar Position, Navigation and Timing, Proceedings of the 2022 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 25-27 January 2022, pp.632-642. https://doi.org/10.33012/2022.18225
Goddard Space Flight Center 2008, A Standardized Lunar Coordinate System for Lunar Reconnaissance Orbiter and Lunar Datasets, NASA Technical Report, 13.
Israel, D. J., Mauldin, K. D., Roberts, C. J., Mitchell, J. W., Pulkkinen, A. A., et al. 2020, LunaNet: a flexible and extensible lunar exploration communications and navigation infrastructure, 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7-14 March 2020, pp.1-14. https://doi.org/10.1109/AERO47225.2020.9172509
Jeong, H., Park, J., Song, J., Kang, M., & Kee, C. 2023, Design of orbit simulation tool for lunar navigation satellite system, Journal of Positioning, Navigation, and Timing, 12, 335-342. https://doi.org/10.11003/JPNT.2023.12.4.335
Johnson, A. E. & Montgomery, J. F. 2008, Overview of Terrain Relative Navigation approaches for precise lunar landing, 2008 IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, pp.1-10. https://doi.org/10.1109/AERO.2008.4526302
Kaplan, E. D. & Hegarty, C. J. 2006, Understanding GPS: Principles and Applications, 2nd ed. (Boston, MA: Artech House).
Murata, M., Akiyama, K., & Naoki, S. 2024, Lunar navigation satellite system for entire moon surface: HDOP and SISE evaluation, Proceedings of the 2024 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 23-25 January 2024, pp.778-786. https://doi.org/10.33012/2024.19495
Murata, M., Kawano, I., & Kogure, S. 2022, Lunar navigation satellite system and positioning accuracy evaluation, Proceedings of the 2022 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 25-27 January 2022, pp.582-586. https://doi.org/10.33012/2022.18220
NASA & ESA 2022, LunaNet Interoperability Specification Document (Version 4).
Pereira, F. & Selva, D. 2020, Exploring the design space of lunar GNSS in frozen orbit conditions, Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20-23 April 2020, pp.444-451. https://doi.org/10.1109/PLANS46316.2020.9110202
Song, J. 2024, A study on orbit design of lunar navigation satellite system for moon exploration, Master’s Thesis, Seoul National University.
Speyerer, E. J. & Robinson, M. S. 2013, Persistently illuminated regions at the lunar poles: Ideal sites for future exploration, Icarus, 222, 122-136. https://doi.org/10.1016/j.icarus.2012.10.010
Taylor, D. B., Bell, S. A., Hilton, J. L., & Sinclair, A. T. 2010, Computation of the Quantities Describing the Lunar Librations in the Astronomical Almanac, Technical Note No.74, pp.1-10. https://apps.dtic.mil/sti/citations/ADA528116
Urrutxua, H. & Lara, M. 2016, Constant, Radial Low-Thrust Problem Including First-Order Effects of J2, Journal of Guidance, Control, and Dynamics, 39, 2763-2768. https://doi.org/10.2514/1.G000598
Vallado, D. A. 2013, Fundamentals of Astrodynamics and Applications, 4th ed. (Portland: Microcosm Press).
Winternitz, L. B., Bamford, W. A., & Price, S. R. 2017, New high-altitude GPS navigation results from the magnetospheric multiscale spacecraft and simulations at lunar distances, Proceedings of the 30th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25-29 September 2017, pp.1114-1126. https://doi.org/10.33012/2017.15367
Ye, H., Guo, H., Liu, G., & Ren, Y. 2018, Observation duration analysis for Earth surface features from a Moon-based platform, Advances in Space Research, 62, 274-287. https://doi.org/10.1016/j.asr.2018.04.029