1Department of Aeronautical and Astronautical Engineering, Korea Aerospace University, Gyeonggi-do 10540, South Korea
2Korea Astronomy and Space Science Institute, Daejeon 34055, Korea
†Corresponding Author: Jeongrae Kim, E-mail: jrkim@kau.ac.kr
Citation: Yoon, S., Kim, Y., Choi, B.-K., Chung, J.-K., & Kim, J. 2025, A Comparative Survey of GPS Midi and Reduced Almanacs, Journal of Positioning, Navigation, and Timing, 14, 139-147.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 June, Volume 14, Issue 2, pages 139-147. https://doi.org/10.11003/JPNT.2025.14.2.139
Received on May 13, 2025, Revised on May 22, 2025, Accepted on May 29, 2025, Published on Jun 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
An analysis was performed on eight parameters constituting the Klobuchar ionosphere model of GPS navigation messages. By analyzing the value of the Klobuchar parameters over a long period of 23 years, the change trend was identified and a correlation with the solar activity index F10.7 was established. Among the Klobuchar parameters, α0 and β0 , which represent the average of the intensity and period of the Klobuchar ionosphere delay function, showed a high correlation with F10.7, while other parameters representing the change in the ionosphere delay value along the geomagnetic latitude showed a very low correlation. Some parameters are characterized by repeated use with very few types of values. A limited number of combinations of αn and βn values were used over 23 years. The combination of Klobuchar parameters thus can be selected by grouping input variable values such as F10.7 or the day number of year and entering them in a simplified form.
GNSS, GPS, ionosphere, Klobuchar model
위성항법시스템 (Global Navigation Satellite System, GNSS) 신호가 대기를 통과할 때 발생하는 신호지연은 전리층에 의한 것과 대류층에 의한 것이 있으며, 적절한 신호지연 보정이 없을 경우 상당한 위치오차를 유발한다. 저가형 단일주파수 GNSS 수신기의 경우 전리층에 의한 신호지연은 수 십 미터의 위치오차를 유발할 수도 있으므로 적절한 신호지연값 보정이 필요하다. 전리층 지연값 보정을 위해 사용하는 모델은 실시간 모델과 후처리 모델로 분류할 수 있는데, 일반적으로 실시간 모델은 후처리모델에 비해 정확도는 낮지만 효용성 측면에서 중요도가 높다. 실시간 모델은 GNSS 항법메시지에 포함되어 제공되는 방식과 Satellite Based Augmentation System (SBAS) 신호 또는 인터넷 등 별도의 데이터링크를 통해 제공되는 방식으로 분류할 수 있다. GNSS 항법메시지에 포함되어 제공되는 전리층 보정정보는 정확도가 높지 않지만, 보정정보 수신을 위한 별도의 데이터링크나 부가장비가 필요하지 않기에 가장 많이 활용되는 방법이다. SBAS 전리층 보정정보는 정확도가 높고 보정정보 간격이 짧지만, SBAS 신호처리 등 부가장비가 필요하다. 후처리 모델은 GNSS 지상관측소의 데이터를 처리하여 필터링한 뒤 제공하는 것으로 International GNSS Service (IGS)에서 제공하는 Global Ionosphere Maps (GIM) 등이 대표적이다. 후처리모델은 정확도는 높지만 실시간으로 사용할 수 없는 단점이 있다. IGS GIM의 경우 2시간 간격으로 보정정보를 제공하므로 5분 간격으로 보정정보를 제공하는 SBAS 전리층 보정정보에 비해 위치추정 정확도는 낮을 수도 있다 (Lee & Park 2025). 장기간 전리층 데이터를 처리하여 생성한 경험적 전리층모델도 많이 사용되는데 International Reference Ionosphere (IRI) 모델 등이 대표적이다. 경험모델의 입력데이터를 실시간으로 입수할 수 있으면, 실시간 모델로 분류할 수도 있지만 모델의 복잡성으로 인한 막대한 연산시간으로 일반적으로 후처리 용도로 주로 사용된다. 이 연구에서는 실시간모델 중 GNSS 항법메시지에 포함된 전리층모델을 중심적으로 다룬다.
항법메시지에 포함된 전리층모델 중 대표적인 것이 Global Positioning System (GPS)에서 사용하는 Klobuchar 모델이다 (Klobuchar 1987). 이는 경험적 전지구 전리층모델인 Bent 모델 (Llewellyn & Bent 1973)을 간략화하여 연산시간을 줄인 모델로 수신기위치의 지방시 (local time), 사용자위치 및 GPS 위성위치만을 입력하면 전리층 지연값을 계산할 수 있는 모델이다. 전리층 지연값을 50% 정도까지 보정하는 것으로 알려져 있으며, Klobuchar 모델을 구성하는 8개 파라미터는 GPS 방송메시지에서 제공하기 때문에 실시간으로 이용 가능하다. Klobuchar 파라미터는 1일 또는 수일 단위로 업데이트되는 값으로 정확히는 실시간 전리층 보정정보보다는 전리층 예측정보에 해당하지만, 실시간으로 사용 가능하므로 실시간 모델로 부르기도 한다. Galileo는 NeQuick-G 형태의 실시간 전리층 보정정보를 제공하는데, 태양활동을 나타내는 3개의 파라미터만으로 전리층 지연값 계산이 가능하다 (European Commission 2016). 전리층 분포를 2차원으로 가정한 Klobuchar 모델에 비해 전리층 분포를 3차원으로 가정한 NeQuick-G 모델은 저궤도위성 등 다양한 분야에서 사용할 수 있고 정확도도 약간 높지만, 연산시간이 Klobuchar 모델에 비해 300배 정도로 훨씬 많이 소요된다는 단점이 있다 (Bak & Kim 2025). 일본 Quasi-Zenith Satellite System (QZSS)은 Klobuchar와 동일한 형식의 파라미터를 전송하는데, QZSS 서비스 지역 내에서만 사용 가능하며, 이외의 지역에서는 GPS Klobuchar 파라미터를 사용하도록 되어 있다 (Cabinet Office 2021, Bak et al. 2023). 중국 BeiDou Navigation Satellite System (BDS)은 두 가지 전리층 모델을 제공하는데, 중국 및 인근지역에 특화된 수정된 Klobuchar 파라미터와 전세계지역을 대상으로 하는 Ionospheric delay correction Model (BDGIM) 파라미터를 제공한다 (China Satellite Navigation Office 2018, Zhao et al. 2020).
본 연구는 실시간 모델 중 GPS Klobuchar의 모델 파라미터에 주안점을 두어 분석을 수행하였다. 그동안 Klobuchar 모델의 성능에 관한 연구는 어느 정도 진행되어 왔다. Swamy et al. (2013)은 저위도 지역에서 Klobuchar 모델과 IRI-2007 모델의 전리층 지연량을 비교하였으며, Stepniak et al. (2014)은 사용자의 위도별로 지자기 활동에 따른 Klobuchar 모델의 변화를 연구하였다. Kim & Kim (2016)과 Kim & Kim (2023)은 Klobuchar 모델 전리층 지연 오차를 전세계 지역에 대해 장기간 데이터를 이용하여 분석하였다.
Klobuchar 모델 파라미터 값은 전세계 전리층 지연값의 관측값을 이용하여 결정할 수 있는데, 최소자승값을 이용한 회귀기법으로 추정 가능하다 (Nishimoto et al. 2013, Zhang et al. 2022, Sim & Park 2025). 하지만, 이는 현재 GPS 항법메시지를 통해 전송되는 Klobuchar 파라미터와는 다른 종류의 파라미터이다. 전리층 지연값의 관측값을 이용하여 결정하는 모델은 후처리 또는 준실시간 모델에 해당하는 것이고, GPS Klobuchar 파라미터는 예측모델이기 때문이다. 관측모델에 비해 예측모델은 F10.7 등 제한된 정보만을 이용하여 생성되기 때문에 전혀 다른 생성기법을 사용하게 된다. GPS가 개발된 1980~1990년대에는 매우 제한된 개수의 GPS 감시국만 운영하였기 때문에 충분한 전리층 지연값을 획득하기 어려웠고, 관측 데이터를 실시간으로 GPS 중앙제어국으로 전송하는 것도 매우 어려운 작업이었다.
예측용으로 GPS Klobuchar 모델 파라미터를 생성하는 알고리즘에 관한 자료는 매우 입수하기 어려운 편이다. 이는 GPS의 각종 항법정보를 생성하는 알고리즘이 대부분 보안 처리되어 발표되지 않는 것과 관련이 있다. Feess & Stephens (1987)는 Klobuchar 모델의 초기 성능을 분석하는 연구에서 기본적인 Klobuchar 파라미터 생성 알고리즘을 언급하고 있다. 이 논문에서는 Klobuchar 파라미터 세트를 미리 생성한 뒤, 특정 입력데이터를 이용하여 파라미터 세트 중에 선택하는 것을 설명하고 있다. 선택된 알고리즘은 항법메시지를 통해 사용자에게 전송된다. 입력데이터로는 태양활동 세기를 나타내는 F10.7과 연중 날짜를 나타내는 Day Of Year (DOY)를 사용하는 것으로 설명되어 있다. 이외에 BDS 전리층모델을 생성하면서 Klobuchar 파라미터 생성기법에 관하여 간접적으로 언급하는 내용이 있기는 하지만 상세한 내용을 포함하고 있지는 않다.
Klobuchar 모델과 유사한 형태의 전리층모델을 생성하려면, Klobuchar 파라미터 생성 알고리즘에 관한 상세한 분석이 필요하다. 기술한 바와 같이 Klobuchar 파라미터 생성에 관한 자료가 부족하므로 Klobuchar 파라미터 값에 대한 분석이 선행될 필요가 있다. 본 연구는 Klobuchar 파라미터 생성기법을 위한 기초 연구로 장기간 Klobuchar 파라미터 데이터를 분석하였다. 2002년부터 2024년까지 23년간 Klobuchar 파라미터 값을 분석하여 각 파라미터의 변화 경향을 분석하고, 태양활동지수와의 상관관계 등을 파악하였다. 이러한 분석을 통해 Klobuchar 파라미터가 특정한 값만으로 구성되어 있다는 것을 파악하고, 향후 Klobuchar 파라미터와 유사한 알고리즘 생성기법 개발 시 도움을 줄 수 있는 기초자료를 확보하였다. 2장에서 Klobuchar 모델식의 구성 및 데이터 분석 기간을 설명한 뒤, 3장에서 23년간 Klobuchar 파라미터 값의 변화와 F10.7 태양활동지수와의 상관관계를 분석하였다. 4장에서는 장기간 데이터 분석으로부터 특정한 Klobuchar 파라미터 값의 조합만 사용된다는 것을 식별하여, 23년간 사용된 Klobuchar 파라미터 값을 분류하였다. 이를 통해 향후 Klobuchar 파라미터 생성에 필요한 기초 자료를 확보하였다.
GPS Klobuchar 모델은 350 km 상공에 위치한 두께가 없는 단일층에 자유전자가 밀집되어 있다고 가정하고, 밤 시간에는 자유전자가 일정한 값을 가진다고 가정하고 있다. 1973년에 개발된 경험적 전지구 전리층모델인 Bent 모델 (Llewellyn & Bent 1973)에 기반을 두고 있으며, 이를 GPS 항법메시지에 탑재할 수 있도록 단순화한 모델이다. GPS 의사거리 신호가 전리층 단일층을 통과하는 Ionospheric Pierce Point (IPP)에서의 전리층 지연값 정보를 제공하는데, 전리층 지연값은 사용자의 지방시가 14시일 때 최댓값을 가지며, 야간에는 일정한 최솟값을 가진다 가정한다.
Fig. 1은 Klobuchar 모델의 진폭과 주기를 나타내고 있다. 진폭이 최대가 되는 시간은 지방시 14시로 고정되어 있으며, 주기는 변경될 수 있다. 야간 시간의 범위는 주기값이 증가함에 따라 축소되게 되지만, 전리층 지연값은 5 ns로 고정되어 있다. 태양활동의 세기가 강한 시점에는 야간에도 전리층 지연값이 5 ns보다 훨씬 크지만 Klobuchar 모델에서는 고정된 5 ns를 사용해야 한다. Klobuchar 모델의 진폭과 주기는 Eqs. (1, 2)에 있는 8개 파라미터로 표현된다.
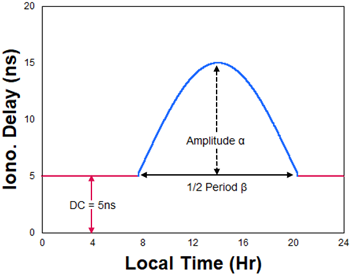
Fig. 1. Klobuchar ionospheric delay model: amplitude and period.
$$A_I = \alpha_0 + \alpha_1 \phi_m + \alpha_2 \phi_m^2 + \alpha_3 \phi_m^3$$
$$P_I = \beta_0 + \beta_1 \phi_m + \beta_2 \phi_m^2 + \beta_3 \phi_m^3$$
여기서, $A_I$는 전리층 지연값의 진폭을 나타내는데, 사용자의 지자기위도 $\phi_m$의 3차 다항식 형태로 표시된다. $\alpha_0$, $\alpha_1$, $\alpha_2$, $\alpha_3$은 다항식 파라미터이며, GPS 항법메시지에서 제공되는 값이다. 이는 지자기위도에 따른 전리층지연값 크기의 변화를 나타내는데 사용된다. PI는 전리층 지연값의 주기를 나타내는데, AI와 동일하게 지자기위도의 3차 다항식 형태로 표현되며, 4개 파라미터 $\beta_0$, $\beta_1$, $\beta_2$, $\beta_3$는 항법메시지에서 제공된다. $A_I$와 $P_I$로부터 전리층지연값을 계산하는 방법은 GPS Interface Control Document (ICD) (ISGPS-800J 2022)에 기술되어 있다.
GPS는 1993년부터 본격 가동하기 시작한 이후 각종 알고리즘의 변경이 있었는데, Klobuchar 전리층모델도 이에 해당한다. Klobuchar 모델 파라미터의 생성기법 등을 분석하기 위해서는 알고리즘 생성기법이 안정된 이후의 데이터만을 이용하는 것이 분석의 난이도를 줄이는 방법이다. 전리층 알고리즘 생성기법 변경에 관하여 미국 GPS 운영국에서의 직접적인 공지는 없으므로, GPS Klobuchar 모델의 성능을 정밀 전리층모델과 비교하는 방법으로 알고리즘 생성기법 변경을 간접적으로 파악하였다.
IGS에서 제공하는 후처리 전리층 지도인 IGS GIM은 전세계 수백 개 IGS 수신국에서 측정한 GPS 이중주파수 신호를 이용하여 생성된 것으로 높은 정확도를 가지므로 본 연구에서 Klobuchar 오차계산 시 기준값으로 사용하였다. IGS GIM은 2.5° 간격 (위도)과 5° 간격 (경도)으로 설정된 격자점에서의 수직지연값을 2시간 간격으로 제공하며, 후처리 방식이므로 최대 11일 후에 제공된다. IGS GIM은 1998년 6월부터 생성되었기 때문에 Klobuchar 모델과 비교는 1998년 이후만 가능하다.
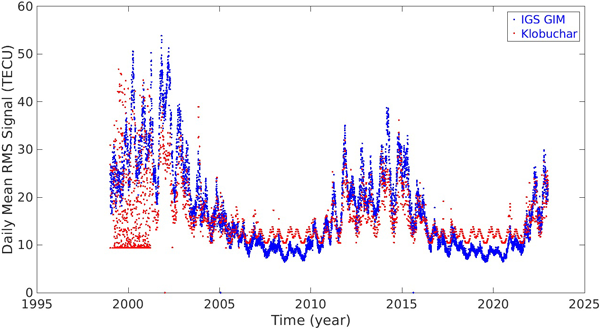
Fig. 2. Daily mean magnitude of the global ionospheric delays by the IGS and Klobuchar models (1999-2022).
Fig. 2는 1999년 1월부터 2022년 12월까지 IGS GIM과 Klobuchar 모델의 전리층 지연값을 비교한 것이다. 2시간마다 전세계 5112개 IGS GIM 격자점에서의 수직 전리층 지연값을 계산한 후 평균값을 TECU단위로 표시하였다. 동일한 격자점에서 Klobuchar 모델을 이용하여 수직전리층 지연값을 계산한 후 평균을 계산하였다. 전체적으로는 Klobuchar 전리층 지연값이 IGS GIM 전리층 지연값과 유사한 경향을 보이지만, 2001년 2월까지는 IGS와 Klobuchar 모델의 차이가 크게 발생하는 것을 볼 수 있다. 정확도가 높은 IGS GIM의 전리층 지연값을 참값으로 가정했을 때, 이와 같은 차이는 Klobuchar 모델의 오차를 의미한다. 2001년 3월 이후부터 Klobuchar 전리층 지연값이 IGS GIM 전리층 지연값을 잘 추종하는데, 이 시기부터 전리층 알고리즘의 주요한 변화는 Klobuchar 파라미터 갱신주기이다. 이론상으로 Klobuchar 파라미터 값은 실시간으로 변경될 수 있지만, 실제 운용 시에는 1일에 한 번 정도 갱신된다. 2001년 2월까지는 거의 매일 파라미터값이 갱신되었지만 2001년 3월 이후에는 최대 10일 또는 20일로 갱신주기가 급격히 증가하였다. 이는 파라미터 생성 알고리즘의 변화를 의미하는데, 결과적으로 Klobuchar 모델의 정확도가 상당히 높아졌음을 알 수 있다. Klobuchar 모델은 예측모델이므로 F10.7 예측정확도 등에 의존하는데, 예측정확도가 높지 않은 경우 잦은 단기예측보다는 간헐적인 장기예측이 통계적으로 우수한 경우가 있는데, 이에 해당된다고 할 수 있다. 즉, 전리층 변화는 예측이 상당히 어려운 분야이므로 간헐적인 장기예측이 적합할 수도 있다. 2001년 3월 이전과 이후로 Klobuchar 파라미터 특성이 상이하므로 두 개 그룹의 데이터를 같이 분석하는 것은 효율적이지 못하다. 또한, 2001년 3월 이후 현재까지는 Klobuchar 파라미터 생성 알고리듬의 큰 변화가 없는 것으로 추측된다. 이러한 이유로 본 연구에서는 GPS Klobuchar 모델 성능분석은 성능이 안정화된 2001년 3월 이후의 데이터만을 이용하여 분석을 수행하였다.
Klobuchar 모델의 $\alpha_n$과 $\beta_n$ 파라미터 생성기법을 연구하기 위한 기본 단계로 αn과 βn 파라미터의 일일 및 연간 변화 경향을 살펴보았다. Klobuchar 파라미터 생성 알고리즘이 안정화된 2002년 1월부터 2024년 12월까지 23년 간 8개 $\alpha_n$과 $\beta_n$ 파라미터의 일일변화를 분석하였다.
Fig. 3은 $\alpha_0$, $\alpha_1$, $\alpha_2$, $\alpha_3$ 진폭 파라미터의 23년간 변화를 나타내고 있다. 전리층 지연값 크기의 평균값을 나타내는 $\alpha_0$는 다양한 값으로 변화하는데, 전체적으로 태양활동 세기 F10.7 변화와 유사하게 2002년과 2013년 근방에서 최댓값을 가지는 형태로 변화함을 알 수 있다. F10.7과의 상관성은 3.2절에서 상세하게 분석하였다. 23년동안 $\alpha_1$, $\alpha_2$, $\alpha_3$ 는 4개에서 7개 사이의 특정한 값만을 가지는 것을 알 수 있다. 특히 $\alpha_2$는 4개 값만을 가지며 파라미터 값이 장기간 변화하지 않는 것을 알 수 있다. $\alpha_1$, $\alpha_3$와 $\alpha_2$ 파라미터의 차이는 다항식의 홀수항 계수와 짝수항 계수이다. 즉, 지자기위도가 음수가 될 때 홀수항의 파라미터 값은 전리층 지연값 세기에 직접적인 영향을 유발하지만 짝수항은 양수값 지자기위도와 동일한 영향을 유발하게 된다. 지자기 적도에 대해 전리층 지연값 세기의 비대칭성이 클수록 홀수항 계수의 크기가 증가하게 된다.
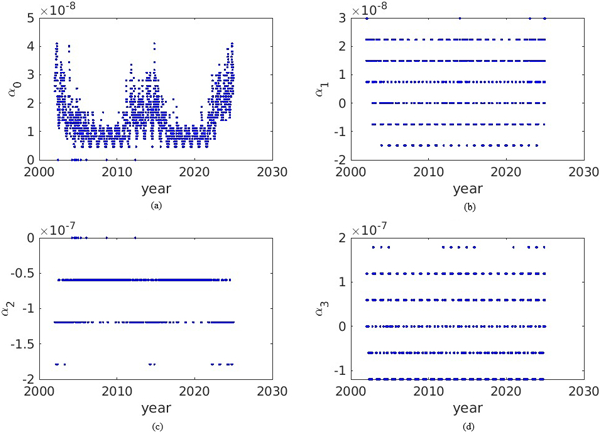
Fig. 3. Daily variation of the Klobuchar magnitude parameters, (a) $\alpha_0$, (b) $\alpha_1$, (c) $\alpha_2$, and (d) $\alpha_3$ (2002-2024).
Fig. 4는 $\beta_0$, $\beta_1$, $\beta_2$, $\beta_3$ 파라미터의 23년간 변화를 나타내고 있다. $\alpha_n$에 비해 $\beta_n$이 좀 더 다양한 값으로 변화하는 것을 알 수 있는데, 전리층 지연값 변화주기의 평균값을 나타내는 $\beta_0$의 경우 $\alpha_0$와 유사한 변화 경향을 나타낸다. $\beta_1$과 $\beta_3$도 어느 정도의 주기성을 나타내면서 $\beta_0$와 유사한 변화성을 나타내는 것을 알 수 있다. $\beta_2$는 $\alpha_2$와 마찬가지로 21년간 7개의 값만을 나타내는데, 이 역시 지자기위도 다항식의 짝수항에 대응하는 파라미터로 지자기위도 북반구와 남반구의 전리층 지연값 변화 형태와 관련이 있는 것으로 생각된다.
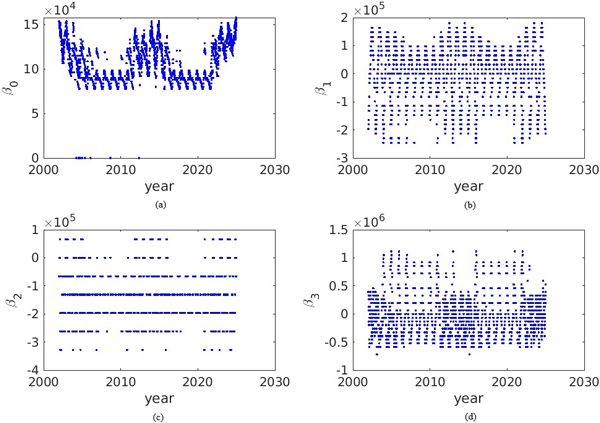
Fig. 4. Daily variation of the Klobuchar period parameters, (a) $\beta_0$, (b) $\beta_1$, (c) $\beta_2$, and (d) $\beta_3$ (2002-2024).
태양활동 세기를 나타내는 F10.7은 Klobuchar 파라미터 생성에 주요한 역할을 하고 있는 것으로 알려져 있으므로 (Klobuchar 1987, Feess & Stephens 1987), 각 파라미터와 F10.7 값과의 상관관계를 분석하였다. 1일 단위로 F10.7과 $\alpha_n$, $\beta_n$ 파라미터 사이의 상관관계를 분석하였는데, 해당 날짜의 F10.7 관측값 대신 직전 날짜의 F10.7 관측값으로부터 추정한 F10.7 예측값을 이용하여 상관관계를 분석하였다. 이는 GPS Klobuchar 모델이 전리층 지연값 관측모델이 아닌 예측한 F10.7 값을 입력으로 사용하기 때문이다 (Feess & Stephens 1987). 직전 5일간의 일일 F10.7 값을 평균하여 해당일의 F10.7 예측값으로 설정하였는데, 이러한 5일 이동평균 역시 Feess & Stephens (1987)에 근거하였다.
Fig. 5는 2002년부터 2024년까지 F10.7 예측값의 변화를 나타낸 것이다. 태양활동 주기인 11년 동안 극대와 극소를 반복하며, 분석 기간 중 극소기는 2008년 및 2020년이고, 극대기는 2002년, 2013년, 2024년이다. 이동평균에 의한 예측값을 사용하는 경우 이동평균 효과에 의해 급격한 F10.7 변화가 줄어들게 된다.
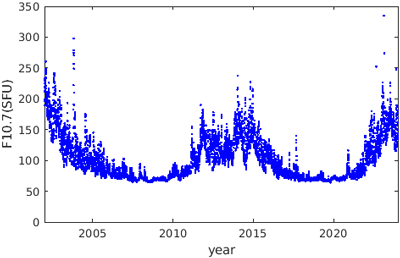
Fig. 5. Daily variation of predicted F10.7 index (2002-2024).
Fig. 6은 2002년부터 2024년까지 $\alpha_0$, $\alpha_1$, $\alpha_2$, $\alpha_3$ 파라미터와 F10.7과의 상관관계 경향을 분석하기 위하여 F10.7 변화에 따른 $\alpha_0$, $\alpha_1$, $\alpha_2$, $\alpha_3$ 파라미터값의 변화를 그래프로 나타낸 것이다. F10.7은 5일 평균에 의한 예측값을 사용하였는데, 해당 날짜의 관측값을 대신 사용하더라도 상관관계 그래프는 큰 차이가 없다. 빨간선은 다항식을 이용한 최소자승법 fitting curve를 나타내는 것으로 제시된 그림은 2차 다항식을 사용하였다. $\alpha_0$는 F10.7로 표현한 fitting curve가 선형에 근접하므로 F10.7과의 상관관계가 높은 것을 알 수 있는데, 이는 $\alpha_0$가 일일 중 전리층 지연값의 최댓값을 나타내기 때문이다. 즉, 태양활동이 강해지면 지구자기장 세기가 증가하고 전리층 지연값이 증가하게 된다. 이에 비해 $\alpha_1$, $\alpha_2$, $\alpha_3$ 파라미터는 F10.7 값에 따라 증가하거나 감소하는 경향이 파악되지 않으므로, F10.7과 명확한 상관관계를 가지지 않는 것으로 보인다. $\alpha_1$, $\alpha_2$, $\alpha_3$는 지자기위도에 따른 전리층 지연값 세기의 변화를 나타내는 것으로 지구자기장 분포와 관련이 있는 값인데, F10.7은 지구자기장과 관련 없이 태양활동만을 나타내기 때문이다. 이러한 분석으로부터 $\alpha_0$는 F10.7 값을 이용하여 어느 정도 회귀 (regression) 모델링을 할 수 있는데, $\alpha_1$, $\alpha_2$, $\alpha_3$는 F10.7 값만으로는 모델링이 어려울 것으로 예상된다.
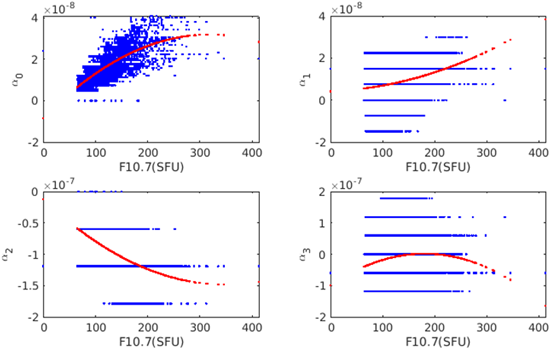
Fig. 6. Correlations between predicted F10.7 and Klobuchar magnitude parameters, $\alpha_0$, $\alpha_1$, $\alpha_2$ and $\alpha_3$ (2002-2024).
Fig. 7은 2002년부터 2024년까지 $\beta_0$, $\beta_1$, $\beta_2$, $\beta_3$ 파라미터와 F10.7 예측값과의 상관관계를 그래프로 나타낸 것으로, 빨간선은 2차 다항식을 이용한 fitting curve를 나타내는 것이다. $\beta_0$는 F10.7과 높은 상관관계를 나타내는데, F10.7 값이 큰 경우에는 $\beta_0$ 값이 정체되거나 감소하는 경향을 보이기도 한다. 태양활동이 강할수록 전리층 지연값이 최솟값을 유지하는 시간이 줄어들기 때문에 주기를 나타내는 $\beta_0$가 증가하는 것으로 생각된다. F10.7과 $\beta_1$ 또는 $\beta_3$의 상관관계는 매우 낮은 것으로 나타나는데, Fig. 4의 시계열데이터 분석 시 $\beta_1$과 $\beta_3$도 $\beta_0$와 유사한 변화 경향을 나타낸 것과는 다른 결과이다.
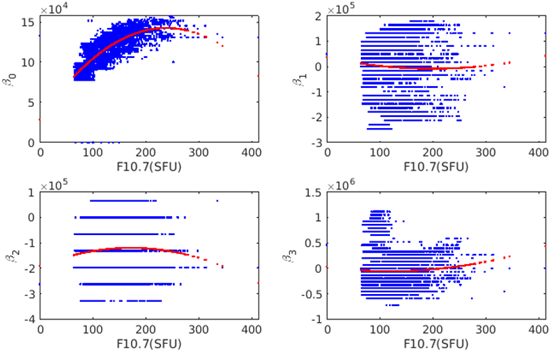
Fig. 7. Correlations between predicted F10.7 and Klobuchar period parameters, $\beta_0$, $\beta_1$, $\beta_2$ and $\beta_3$ (2002-2024).
GPS 항법메시지의 Klobuchar 파라미터는 반복되는 값이 많이 사용되고 있으므로, 이를 분류화하여 특정 값의 발생빈도 등을 파악하는 것이 필요하다. 이를 위해 23년간 데이터를 분석하여 각 파라미터 별로 사용된 값의 개수를 분석하였다.
Table 1은 2002년부터 2024년까지 사용된 $\alpha_n$과 $\beta_n$ 파라미터의 개수를 나타내고 있다. $\alpha_0$와 $\beta_0$는 동일한 빈도를 나타내고 있는데, 23년의 8400일 중 42개의 값만 사용된 것을 의미한다. $\beta_1$과 $\beta_3$은 $\beta_0$보다는 빈도가 적지만 30개와 31개의 값이 사용되었다. $\alpha_1$, $\alpha_2$, $\alpha_3$와 $\beta_2$는 5개에서 10개로 매우 작은 종류의 값만이 사용되었음을 알 수 있다. $\alpha_1$, $\alpha_2$, $\alpha_3$에 비해 $\beta_1$, $\beta_2$, $\beta_3$이 사용된 종류가 많다는 것은 지자기 위도에 따른 주기값의 변화 형태가 진폭의 변화 형태에 비해 자주 변경된다는 것을 의미한다.
Table 1. Number of distinct Klobuchar parameters used from 2002 to 2024.
| α0 | α1 | α2 | α3 | β0 | β1 | β2 | β3 | |
|---|---|---|---|---|---|---|---|---|
| Number of distinct values | 42 | 7 | 5 | 8 | 42 | 30 | 10 | 31 |
Fig. 8은 1999년부터 2024년까지 매년 사용된 $\alpha_0$, $\alpha_1$, $\alpha_2$, $\alpha_3$와 $\beta_0$, $\beta_1$, $\beta_2$, $\beta_3$ 파라미터의 수를 나타내고 있다. 즉, 파라미터 별로 1년간 사용된 값을 분류한 뒤 구분되는 파라미터 수를 그래프로 나타낸 것이다. 1999년과 2000년에는 거의 매일 파라미터의 값이 변화하는 데 비해, 2002년부터는 연간 사용되는 파라미터의 종류가 급격히 감소함을 알 수 있다. 이는 Fig. 1에서 2001년 3월부터 Klobuchar 모델의 모델링오차가 급격히 줄어든 것과 관련이 있는 것으로 생각된다. 2001년 2월까지는 태양활동 및 전리층변화에 따라 매일 Klobuchar 파라미터를 갱신하였으나, 전리층 지연값 오차는 오히려 증가하는 문제가 있어서 일정한 범위에서 변화하는 간략한 전리층모델로 전환한 것으로 생각된다. 사용된 파라미터의 수는 2002년과 2013년 등 태양활동 극대기에 증가하는데, 태양활동이 강할수록 전리층 지연값의 세기도 커지므로 이를 나타내기 위한 파라미터 값의 종류도 증가하는 것으로 생각할 수 있다.
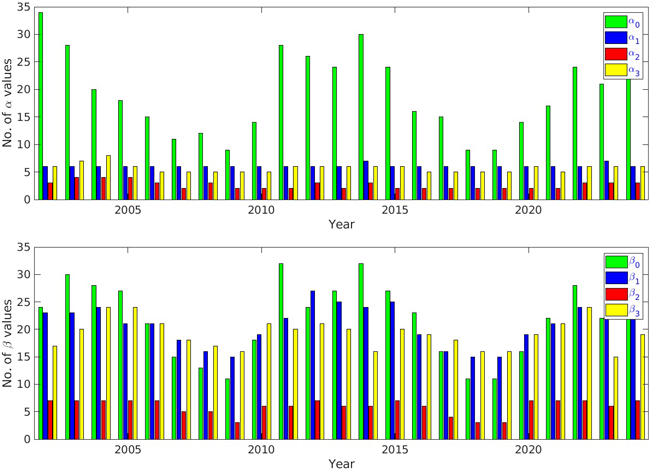
Fig. 8. Annual number of distinct values of the GPS Klobuchar amplitude (top) and period (down) parameters used from 2002 to 2024.
8개 $\alpha_n$과 $\beta_n$ 파라미터 값의 조합을 1개의 세트로 정의한 뒤 서로 다른 값을 가지는 세트 수를 분석하였다. 즉, $\alpha_0$, $\alpha_1$, $\alpha_2$, $\alpha_3$와 $\beta_0$, $\beta_1$, $\beta_2$, $\beta_3$의 8개 파라미터 중 1개의 값이라도 다른 값을 가지면 새로운 세트로 설정한 뒤 고유번호를 부여하였다.
Fig. 9는 2002년부터 2024년까지 매일 사용된 Klobuchar 파라미터 세트별로 번호를 부여한 것이다. 2002년 1월 1일에 사용된 세트에 1번을 부여하였는데, 4일 동안 동일한 값이 사용되다가 1월 5일에 값이 변화하였으므로 1월 5일의 파라미터 조합을 2번 세트로 설정하였다. 이러한 방법으로 이전에 사용되지 않은 파라미터 값의 조합이 나타나면 새로운 세트 번호를 부여하였다. 2002년의 경우 총 123개 세트가 사용되었으며, 2003년에는 2002년에 사용된 세트가 반복되다가 새로운 세트가 생성되었다. 태양활동 극소기인 2005년과 2010년 사이에는 한정된 파라미터 세트만 사용된 것을 알 수 있는데, 이는 전리층 지연값 변화폭이 작아서 적은 종류의 파라미터 세트만 필요하기 때문이다. 전리층 극대기에 세트의 범위가 증가하는데, F10.7 변화와 매우 유사함을 알 수 있다. 마지막 세트 번호는 355로 이는 23년간 총 8400일 중 불과 355개의 파라미터 세트만 반복해서 사용되었음을 의미한다.
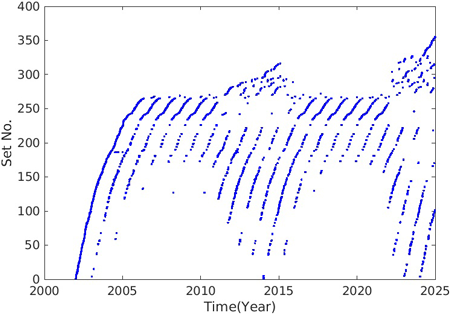
Fig. 9. Daily parameter set number of the Klobuchar parameters.
Fig. 10은 2002년부터 2024년까지 연간 새로 부여된 파라미터 세트 수를 나타내고 있다. 2002년에는 분석 첫해이므로 106개 세트가 사용되었는데 이는 평균 3일에 1개 세트가 사용되었음을 의미한다. 2년차인 2003년에는 2002년과 반복되지 않는 세트 수가 70개로 감소하였으며, 이후 매년 새로운 세트의 수가 감소함을 알 수 있다. 새로운 세트의 수는 태양활동 극소기인 2007년부터 2010년 사이에는 매년 0~1개 정도로 낮은 값을 보이다가 2010년부터 2013년 사이에 새로 생성되었다. 2016년부터 2021년 사이에는 새로운 세트가 전혀 사용되지 않았으나, 2022년부터 전리층 지연값 크기의 범위가 증가하면서 새로운 세트가 증가함을 알 수 있다.
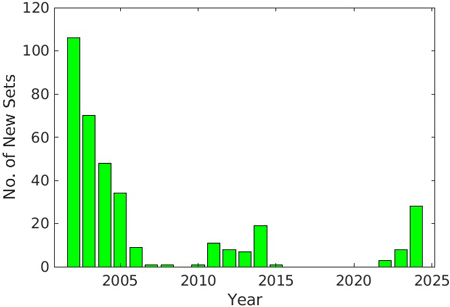
Fig. 10. Annual number of new Klobuchar parameter sets introduced each year.
Fig. 11은 2002년부터 2024년까지 매년 사용된 Klobuchar 파라미터 세트의 수를 나타내는 것으로, 일일 F10.7 값과 같이 도시하였다. 태양활동 극대기에 사용되는 파라미터 세트의 종류가 증가하는 등, F10.7과의 상관관계가 매우 높은 것을 볼 수 있다. 이로부터 파라미터 세트를 구분하는 입력값으로 F10.7이 사용되는 것을 추정할 수 있다.
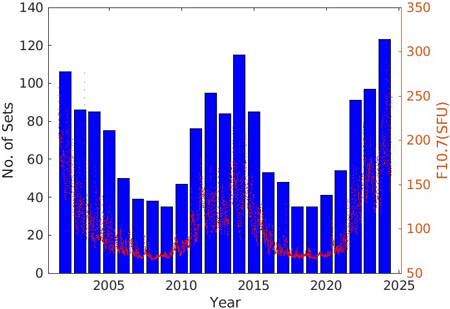
Fig. 11. Annual number of Klobuchar parameter sets used each year.
Klobuchar 파라미터 조합에 대한 분석 결과를 이용하여 미래 Klobuchar 파라미터 예측 가능성을 시험하였다. 입력데이터로부터 특정 Klobuchar 파라미터 조합을 선택하는 알고리즘을 도출할 수 있으면, 이를 활용하여 미래의 Klobuchar 파라미터 방송값을 예측하는 것이 가능하다. 이러한 알고리즘을 응용하여 자체적인 전리층 지연값 데이터베이스를 구축한 뒤 이로부터 Klobuchar와 유사한 파라미터를 생성하는 것도 가능하기 때문이다. 다수의 GNSS 지상감시국 관측값으로부터 Klobuchar 파라미터를 최소자승법으로 추정하는 방법은 관측시점(과거)의 전리층 지연값을 나타내는 값이므로, 미래의 전리층 지연값을 표현하기 위해서는 Klobuchar 파라미터를 예측하는 추가 과정이 필요하다. 이에 비해 Klobuchar 파라미터 조합을 사용하는 방법은 소수의 입력데이터만을 예측하면 되기 때문에 훨씬 구현이 간단한 장점이 있다. Klobuchar 파라미터 값의 안정성 측면에서도 Klobuchar 파라미터 추정방법은 관측데이터의 오차에 영향을 받을 수 있고, 개별 파라미터 추정 시 오류가 발생할 수 있으므로, Klobuchar 파라미터 조합방법이 더 안정성이 높은 장점이 있다.
Klobuchar 파라미터 생성 알고리즘을 설명한 논문은 매우 적은데, 본 연구에서는 Feess & Stephens (1987)을 참조하였다. 이 논문은 GPS 개발초기에 Klobuchar 모델 성능분석을 수행하면서 작성한 논문인데, Klobuchar 모델 파라미터에 관해 다음과 같이 설명하고 있다.
(1) 370개의 $\alpha_n$과 $\beta_n$ 파라미터 세트 중에서 선택하여 방송
(2) 37개 날짜 그룹을 입력값으로 사용
(3) 10개의 F10.7 그룹을 입력값으로 사용
(4) 5일 평균 F10.7 값을 예측값으로 사용
이 논문은 GPS 개발 초기인 1987년에 발표된 논문으로 1990년대이후로 Klobuchar 파라미터 생성기법에 상당한 변화가 있었기 때문에, 현재 Klobuchar 파라미터 구성을 나타내지는 않는 것으로 파악된다. 하지만 어느 정도 연관성은 존재할 것으로 생각되어 이를 근거로 Klobuchar 파라미터 세트를 분류화 하는 시험을 수행하였다. F10.7 그룹과 날짜그룹 중 날짜그룹은 추론하기가 비교적 용이한데, 37개의 날짜그룹은 DOY를 10일 간격으로 구성하였을 것으로 추정되는 항목이다. DOY 그룹의 시작일을 1일로 설정할 경우, 1~10일, 11~20일, …, 361~365일 등이다. 물론 DOY 시작일이 1일이 아닐 가능성도 있다.
Fig. 12는 2002년부터 2024년까지 10일 간격으로 DOY 그룹을 구분한 뒤, 해당 DOY 그룹별로 사용된 Klobuchar 파라미터 세트 수를 나타낸 것이다. 만약 Feess & Stephens (1987) 논문과 같이 37개 DOY 그룹과 10개 F10.7 그룹만 입력으로 사용되었을 경우, DOY 그룹별로 최대 10개 세트의 값만 사용되어야 하지만, 분석결과 DOY 11~20일 그룹에서 최대 25개 세트가 사용되었다. 이는 DOY 분류가 잘못되었을 가능성이 있는데, 우선 DOY 그룹의 시작일이 1월 1일이 아니거나, 그룹 간격이 10일이 아닐 가능성이 있다.
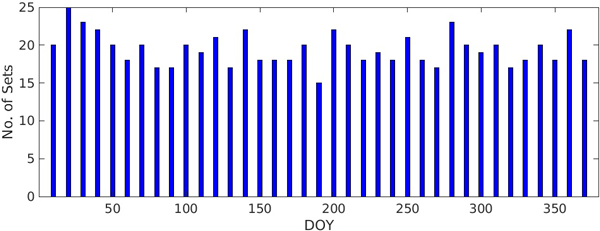
Fig. 12. Number of Klobuchar parameter sets used in each 10-day DOY group (2002-2024).
DOY 그룹 형성방법을 좀 더 살펴보기 위하여 10일치 DOY 그룹대신 1일 간격으로 사용된 파라미터 세트를 계산해 보았다. Fig. 13은 2002년부터 2024년까지 DOY 별로 사용된 Klobuchar 파라미터 세트 수를 나타낸 것이다. 1일치로 분류해도 최대 12개의 세트가 사용된 것을 알 수 있다. 이런 분석을 통해 DOY 그룹설정에는 추가 연구가 필요할 것으로 생각된다. F10.7 그룹설정은 DOY 그룹보다 더욱 어려운 작업인데, 10개 그룹을 분류하는 기준에 관한 추측할 만한 근거가 없기 때문이다. 또한, F10.7 그룹설정보다 비교적 간단한 DOY 그룹설정이 명확하지 않은 상태에서는 F10.7 그룹설정을 하기 어려운 면이 있다.
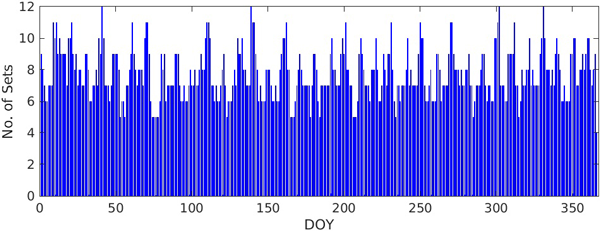
Fig. 13. Number of Klobuchar parameter sets used in each day (2002-2024).
DOY그룹설정과 F10.7 그룹설정은 현재로서는 명확하게 식별되지는 않지만, 2002년부터 23년간 355개의 Klobuchar 파라미터 세트만 사용된 것을 고려할 때, 입력 조건에 따라 사전에 설정된 특정한 파라미터 세트만 사용되는 것으로 판단된다. DOY 및 F10.7 입력변수 외에 지자기계수 변화 등 다른 입력변수가 있을 가능성이 있는데, 이를 파악하기 위해서는 해당 시험변수와의 상관성 분석 등이 필요하다.
GPS 항법메시지의 Klobuchar 전리층모델을 구성하는 8개 파라미터에 대한 분석을 수행하였다. 이는 향후 Klobuchar 전리층모델과 유사한 예측모델을 개발할 경우에 기초 자료로 사용할 수 있다. 2002년부터 2024년까지 장기간 Klobuchar 파라미터 값을 분석하여 파라미터 변화 경향을 파악하고, 태양활동지수인 F10.7과의 상관관계를 파악하였다. Klobuchar 파라미터 중 전리층 지연값 함수 진폭의 세기와 주기의 평균을 나타내는 $\alpha_0$과 $\beta_0$은 F10.7과 높은 상관관계를 보인다. 반면에, 지자기위도에 따른 전리층 지연값 변화를 나타내는 $\alpha_1$, $\alpha_2$, $\alpha_3$나 $\beta_1$, $\beta_2$, $\beta_3$는 F10.7과 매우 낮은 상관관계를 보인다. 또한, $\alpha_1$, $\alpha_2$, $\alpha_3$는 매우 적은 종류의 값만 반복해서 사용되는 특징이 있다.
이러한 파라미터 데이터 분석을 통해 특정한 $\alpha_n$과 $\beta_n$ 값의 조합만이 사용된다는 것을 파악하였다. 2002년부터 23년간 총 355개의 $\alpha_n$과 $\beta_n$ 값의 조합만이 사용되었는데, 이는 F10.7나 연간 날짜수 등 입력변수값을 그룹화하여 단순화된 형태로 입력하는 것을 시사한다. 즉, 입력조건을 단순화한 뒤 이를 통해 간단하게 미리 설정한 Klobuchar 파라미터 세트를 출력하는 것으로 생각된다. 향후 입력변수값을 그룹화 등에 관한 추가연구를 수행하면 Klobuchar와 유사한 수준의 전리층 예측모델을 구현하는 것도 가능할 것으로 생각된다.
Conceptualization, J.K.; formal analysis, S.Y. and J.K.; data curation, S.Y. and Y.K.; writing—original draft preparation, S.Y. and J.K.; writing—review and editing, J.K.; project administration, B.C., J.C., and J.K.; funding acquisition, B.K. and J.C.
The authors declare no conflict of interest.
Bak, S., Kim, B., Kim, S.-K., Bu, S. C., & Lee, C. S. 2023, Ionospheric Model Performance of GPS, QZSS, and BeiDou on the Korean Peninsula, Journal of Positioning, Navigation, and Timing, 12, 113-119. https://doi.org/10.11003/JPNT.2023.12.2.113
Bak, S. & Kim, J. 2025, Performance Analysis of Modified Nequick G Ionosphere Models for Low Earth Orbiting Satellites, Advances in Space Research, 75, 5544-5558. https://doi.org/10.1016/j.asr.2025.01.030
Cabinet Office 2021, Quasi-Zenith Satellite System Interface Specification Satellite Positioning, Navigation and Timing Service, Government of Japan National Space Policy Secretariat, IS-QZSS-PNT-004.
China Satellite Navigation Office 2018, BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B3I, BeiDou Navigation Satellite System, Version 1.0. http://www.beidou.gov.cn/xt/gfxz/201802/P020180209623601401189.pdf
European Commission 2016, European GNSS (Galileo) Open Service Ionospheric Correction Algorithm for Galileo Single Frequency Users, European Union Agency for the Space Programme, Issue 1.2, https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo_Ionospheric_Model.pdf
Feess, W. A. & Stephens, S. G. 1987, Evaluation of GPS ionospheric time-delay model, IEEE Transactions on Aerospace and Electronic Systems, 23, 332-338. https://doi.org/10.1109/TAES.1987.310830
IS-GPS-800J 2022, Global Positioning System Directorate Systems Engineering & Integration Interface Specification, IS-GPS-800J, Navstar GPS Space Segment / User segment L1C interfaces, USA: Navstar GPS Joint Program Office. https://www.gps.gov/technical/icwg/IS-GPS-800J.pdf
Kim, J. & Kim, Y. 2023, Long-term Analysis of Availability and Accuracy Variation of GPS Ionospheric Delay Model, Journal of Advanced Navigation Technology, 27, 841-848. https://doi.org/10.12673/jant.2023.27.6.841
Kim, M. & Kim, J. 2016, A long-term accuracy analysis of the GPS Klobuchar ionosphere model, Journal of the Korean Society for Aviation and Aeronautics, 24, 11-18. https://doi.org/10.12985/ksaa.2016.24.2.011
Klobuchar, J. A. 1987, Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users, IEEE Transactions on Aerospace and Electronic Systems, AES-23, 325-331. https://doi.org/10.1109/TAES.1987.310829
Lee, H.-S. & Park, K.-D. 2025, Performance Analysis of GIM and SBAS Ionosphere Modeling for GPS Positioning in the Korean Peninsula, Journal of Positioning, Navigation, and Timing, 14, 91-99. https://doi.org/10.11003/JPNT.2025.14.1.91
Llewellyn, S. K. & Bent, R. B. 1973, Documentation and description of the Bent ionospheric model, Defense Technical Information Center. https://apps.dtic.mil/sti/pdfs/AD0772733.pdf
Nishimoto, K., Ohashi, M., Kubo, Y., & Sugimoto, S. 2013, Refining the Klobuchar Ionospheric Model with Spherical Cap Harmonic Model for GNSS Positioning, Proceedings of the ISCIE International Symposium on Stochastic Systems Theory and its Applications, Tokyo, Japan, 1-2 November 2012, pp.236-243. https://doi.org/10.5687/sss.2013.236
Sim, E.-J. & Park, K.-D. 2025, Simultaneous Estimation of the Night Delay Constant and Coefficients of a Regional Klobuchar Model Using IGS GIM, Journal of Positioning, Navigation, and Timing, 14, 29-35. https://doi.org/10.11003/JPNT.2025.14.1.29
Stepniak, K., Wielgosz, P., & Paziewski, J. 2014, Accuracy analysis of the Klobuchar ionosphere model transmitted by the GPS system, In proceedings of the 9th International Conference Environmental Engineering, Vilnius, Lithuania, 22-23 May 2014, pp.1-6.
Swamy, K. C. T., Sarma, A. D., Srinivas, V. S., Kumar, P. N., & Rao, P. V. D. S. 2013, Accuracy evaluation of estimated ionospheric delay of GPS signals based on Klobuchar and IRI-2007 models in low latitude region, IEEE Geoscience and Remote Sensing, 10, 1557-1561. https://doi.org/10.1109/LGRS.2013.2262035
Zhang, Q., Liu, Z., Hu, Z., Zhou, J., & Zhao, Q. 2022, A Modified BDS Klobuchar Model Considering Hourly Estimated Night-Time Delays, GPS Solutions, 26, 49. https://doi.org/10.1007/s10291-022-01236-0
Zhao, K., Yan, W., Yang, X., Yang, H., & Wei, P. 2020, BDGIM Performance evaluation based on iGMAS global tracking network, Advances in Space Research, 66, 2168-2178. https://doi.org/10.1016/j.asr.2020.07.037