1Department of Geoinformatic Engineering, Inha University, Incheon 22212, Korea
2PP-Solution Inc., Seoul 08504, Korea
†Corresponding Author: Kwan-Dong Park, E-mail: kdpark@inha.ac.kr
Citation: Lee, H.-S., Han, J.-M., & Park, K.-D. 2025, Development of Weighting Model Considering Range, Elevation Angle, and SNR for Multi-GNSS PPP, Journal of Positioning, Navigation, and Timing, 14, 149-155.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 June, Volume 14, Issue 2, pages 149-155. https://doi.org/10.11003/JPNT.2025.14.2.149
Received on May 27, 2025, Revised on Jun 02, 2025, Accepted on Jun 05, 2025, Published on Jun 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Multi- Global Navigation Satellite System (GNSS) integration is widely recognized as an effective approach to improve positioning accuracy and reduce convergence time. However, issues of performance degradation regarding certain satellite constellations have been raised, particularly some BeiDou satellites in Geostationary Earth Orbit (GEO), due to orbitrelated errors. To address this, the present study proposes a novel weighting model that maintains the advantages of multiGNSS integration while minimizing the adverse effects by applying differential weights based on satellite constellation characteristics. The proposed model calculates satellite weights by comprehensively considering satellite-to-receiver range, elevation angle, and signal-to-noise ratio (SNR), and quantitatively reflects the physical characteristics of each constellation— Medium Earth Orbit (MEO), Inclined Geosynchronous Orbit (IGSO), and GEO. Using GNSS data collected over a 12-hour period, this study applies a least-squares-based Precise Point Positioning method using pseudorange measurements with State Space Representation (SSR) corrections. The positioning performance of two weighting strategies is compared: one using elevation and SNR, and the other incorporating range, elevation, and SNR. The results show that the model considering all three factors—range, elevation, and SNR—improved the average positioning accuracy by 3.1%, with a maximum improvement of 9.7%. Additionally, a low standard deviation of 4.1% indicates consistent performance enhancement, and demonstrates the effectiveness of the proposed differential weighting approach.
multi-GNSS, least squares estimation, code pseudorange, PPP
Standard Point Positioning (SPP)와 Precise Point Positioning (PPP) 같은 다양한 위치결정 기법에서 측위 정확도를 높이고, 수렴 시간을 단축하기 위하여 다중 위성 항법의 활용이 고려된다. 다중 위성의 관측 데이터를 사용하면 가용 위성 수가 증가하여 측위 정확도 향상뿐만 아니라 초기 수렴 시간의 단축에도 크게 기여할 수 있기 때문이다 (Cai & Gao 2007, Li et al. 2009). 특히 Global Positioning System (GPS), Galileo, BeiDou와 같은 주요 Global Navigation Satellite System (GNSS) 시스템을 모두 사용하면 측위 성능 개선의 효과가 크다는 점에서 많은 연구가 이루어져 왔다. Choi et al. (2015a)은 GPS, GLObal NAvigation Satellite System (GLONASS), BeiDou, Quasi-Zenith Satellite System (QZSS) 위성의 다양한 조합으로 측위 결과를 분석하였으며, 4개 위성군을 모두 사용한 경우에서 GPS를 단독으로 사용한 경우보다 측위 정확도가 높다는 결과를 보인다. 또한 Li et al. (2015)는 GPS, GLONASS, Galileo, BeiDou 위성을 이용한 GNSS PPP 모델을 개발하여 다중 위성 항법으로 초기 수렴 시간을 단축할 수 있음을 보인다.
그러나 다중 위성군을 활용하는 것이 항상 성능 개선으로 이어지는 것은 아니다. BeiDou 위성만을 사용하여 처리한 PPP 결과에서는 수평 방향 성분에서 평균적으로 2 cm 미만, 수직 방향 성분에서는 약 3 cm의 높은 측위 정확도를 보이지만 (Choi et al. 2015b), GPS, Galileo 위성과 같이 사용하게 되면 일부 상황에서 오히려 측위 성능 저하 요인으로 작용한다. 특히 Geostationary Earth Orbit (GEO) 위성에 해당하는 BeiDou C01~C05의 궤도 오차가 그 주요 원인으로 지목된다 (Tan et al. 2016). 또한 다중 위성 항법을 적용하였을 때, 수렴 시간이 단축되는 것에 비해 측위 정확도는 GEO 위성에 의하여 크게 개선되지 않는다 (Choi et al. 2017a). 이러한 이유로 위성군별 특성을 반영하여 가중값을 차등적으로 부여하는 방법에 대한 연구가 필요하다. 다중 위성 항법을 적용한 칼만 필터 기반의 PPP에서 성능 향상을 위한 연구를 진행한 사례가 존재하나 (Choi et al. 2017b), 최소 제곱 기반의 정밀 단독 측위에 이러한 차등 가중값 모델을 적용한 선행 연구는 전무하다. 또한 Signal In Space Ranging Error (SISRE)에 따라 위성별 가중값을 차등 적용하는 연구가 진행된 바 있는데 (Kazmierski et al. 2018), 해당 연구에서 GEO 위성은 궤도오차에 의해 SISRE가 크므로 가중값을 낮게 부여해서 정확도를 약 40% 개선하고, 수렴 시간을 약 40% 이상 단축한 결과를 확인하였다. 이러한 연구는 위성별 가중값 차등적용이 측위 정확도 향상과 수렴 시간 단축에 기여할 수 있음을 보인다.
따라서, 본 논문에서는 다중 위성 항법의 장점을 유지하면서 성능 저하 요소를 배제하기 위한 방법으로, 위성군을 GPS, Galileo, BeiDou의 Medium Earth Orbit (MEO), GEO, Inclined Geosynchronous Orbit (IGSO)로 구분하여 각 위성에 차등적인 가중값을 부여할 수 있는 새로운 모델을 제안하고자 한다. 2장에서는 단일 가중값 모델의 구조와 한계를 설명하고, 3장에서는 위성과의 거리, 고도각 및 Signal to Noise Ratio (SNR)을 모두 고려한 위성군별 차등 가중값 적용 모델을 설명한다. 4장에서는 제안된 가중값 모델의 성능 입증을 위한 실험 결과를 다루며, 마지막으로 5장에서는 분석 결과와 향후 연구 방향을 논의한다.
이번 장에서는 단일 가중값 모델들을 설명한다. 2.1절에서는 위성의 고도각 기반 가중값 모델을, 2.2절에서는 SNR 기반 가중값 모델을 설명하며, 각 절에서 모델이 가지는 장점과 한계를 기술한다.
위성의 고도각에 기반한 가중값 모델은 GNSS 관측값의 신뢰도를 평가하고 잡음 수준을 추정하는 데 널리 활용되어 왔다. 고도각이 높을수록 대기권을 통과하는 경로가 짧아져 대류권 및 전리층에 의한 지연 오차의 영향을 덜 받고, 또한 건물이나 지형 등에 의한 다중경로 오차가 줄어드는 특성이 있다. 이러한 이유로 고도각이 높은 위성일수록 관측값에 더 높은 신뢰도를 부여하고, 낮은 고도각의 위성은 상대적으로 낮은 가중값을 부여하는 방식이 일반적이다 (Kim 2015). 고도각 기반 가중값 모델은 Eq. (1)과 같으며, Fig. 1은 고도각에 따른 가중값 변화를 나타낸다.
$$W_E = \sin(E)$$
여기서 E와 W는 각각 위성의 고도각과 가중값을 의미한다. 그러나 이러한 방식은 고도각만을 단일 기준으로 사용하므로, 위성의 궤도 유형이나 동적 특성에 따른 신호 품질의 차이를 충분히 반영하지 못하는 한계가 존재한다. 예를 들어, GEO 위성은 특정 위치에 장시간 머무르기 때문에 고도각이 항상 높게 유지되지만, 실제로 수신기에 수신되는 관측값은 낮은 궤도 정밀도나 신호 세기 저하로 인하여 신뢰도가 낮다. 반면, IGSO 위성은 MEO 위성과는 다른 주기적 패턴을 가지며, 특정 지역에서는 상대적으로 낮은 고도각만 확보되는 경우도 있다. 따라서 GEO 위성과 IGSO 위성에는 Eq. (1)을 가중값 모델로 사용할 수 없다. 이처럼 궤도 특성이 서로 다른 위성군을 고도각만으로 평가하는 것에는 한계가 존재한다.
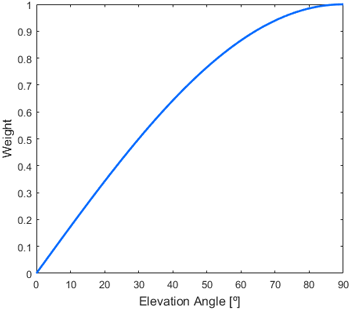
Fig. 1. Variation in weight according to elevation angle.
GNSS 관측값의 신뢰도를 판단하는 또 다른 지표로는 SNR이 있다. SNR은 위성에서 수신기로 전달되는 신호의 강도와 잡음의 비율을 나타내며, 일반적으로 값이 높을수록 수신된 신호의 품질이 우수함을 의미한다 (Kim 2015). SNR은 Carrier to Noise ratio (C/N0)와 유사하게 사용되지만, SNR은 측정에 존재하는 노이즈 수준을 나타낼 수 있는 반면, C/N0는 단위 대역폭당 반송파 대 잡음 비로, 신호 품질을 간접적으로 평가하는 지표이며 노이즈 수준을 나타낼 수는 없다 (Joseph 2010). 또한 SNR은 수신 환경에 따라 민감하게 반응하는 특성으로 인하여 도심이나 수목 지역, 실내환경 등 다양한 조건에서 관측값의 품질을 정량적으로 평가할 수 있다. SNR 기반 가중값 모델은 Eq. (2)와 같으며, Fig. 2는 SNR 값에 따른 가중값 변화를 나타낸다.
$$W_S = \frac{S}{60}$$
여기서 S는 dB 단위의 SNR 값을 의미한다. 또한 SNR 값은 낮을수록 관측 잡음이 증가하여 (Park & Park 2024) 측위 정확도를 저하시킬 수 있는 요소로 작용하고, 60 dB 이상의 값은 도출되지 않으므로 이를 수신 신호 세기의 최대값으로 설정하였다. SNR 기반 가중값 모델은 관측 값마다 실시간 신호 품질을 반영한다는 장점이 있으며, 고도각과는 달리 위성의 기하학적 특성에 영향을 받지 않고 순수하게 수신기 입장에서의 신호 상태를 나타낸다.
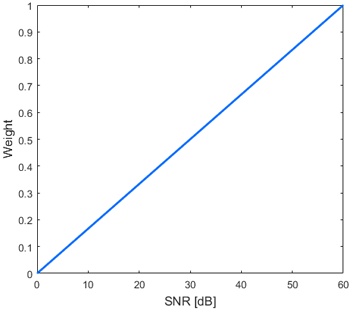
Fig. 2. Variation in weight according to SNR.
하지만 SNR 기반 가중값 모델에도 한계는 존재한다. SNR 값은 수신기 제조사 및 모델에 따라 측정 기준과 스케일이 다를 수 있으며, 일관된 기준이 부족하다. 또한 대부분의 상용 수신기에서는 SNR 최대값이 60 dB 이하 수준이며, 해당 값 이상을 기록하는 경우는 없다. 이로 인하여 SNR을 정규화하여 가중값으로 변환할 때 분포가 지나치게 좁아지는 경향이 있으며, 가중값 간 차별성이 약화된다. 또한 SNR은 위성 신호 자체의 품질보다는 수신기와 안테나 상태, 주위 환경, 간섭 등 외부 요인에 의해 변동되기 쉬우므로, 오차 원인의 근본적인 구분이 어렵다는 단점이 존재한다.
국내에서 GNSS 측위에 활용 가능한 위성군은 서로 다른 궤도 유형을 가지므로, 수신되는 신호의 품질에 따른 정확도 차이를 유발한다. GPS 및 Galileo는 MEO 위성을 사용하고, BeiDou는 MEO 위성 외에도 IGSO와 GEO 위성을 사용한다. 이러한 특성은 측위 정확도에 영향을 미치므로, 앞서 2장에서 설명한 단일 가중값 모델을 적용하는 방식에는 한계가 존재한다. 따라서 이번 장에서는 위성군별 특성을 고려한 차등 가중 값 모델을 제안한다. 3.1절에서 위성과의 거리를 이용한 조정 계수 설정에 대하여 설명하고, 3.2절에서는 위성과의 거리, 고도각 및 SNR을 모두 반영한 가중값 모델을 제안한다.
위성과 수신기의 거리는 신호 품질에 영향을 미치므로, 이를 고려하는 것은 매우 중요하다. GPS 위성과의 거리는 약 20,200 km, Galileo 위성은 약 23,200 km, BeiDou의 MEO 위성은 약 21,500 km 수준으로, 이는 30,000 km를 초과하는 IGSO 및 GEO 위성에 비해 상대적으로 짧다. 이에 따라 위성과의 거리를 기반으로 조정계수를 설정하면, Eq. (3)과 같다.
$$CSC = \frac{1}{D} \cdot 10^7$$
여기서 Constellation-Specific Coefficient (CSC)는 조정 계수를 의미하고, D는 위성과 수신기 간의 미터 단위 거리이며, 소수 첫째 자리부터 표현하기 위하여 107을 곱한다. 해당 식에 따라 MEO 위성은 약 0.4의 CSC를 가지게 되고, GEO 및 IGSO 위성은 약 0.2~0.3의 CSC를 가지게 된다. 또한 계산된 CSC는 0.5를 넘지 않으며 위성군 별로 다른 값을 가지므로, 위성군 별 특성을 고려한 요소로 활용될 수 있다. Fig. 3은 2025년 4월 20일 (DOY 110) 정오부터 한시간 동안 계산된 CSC를 나타낸다.
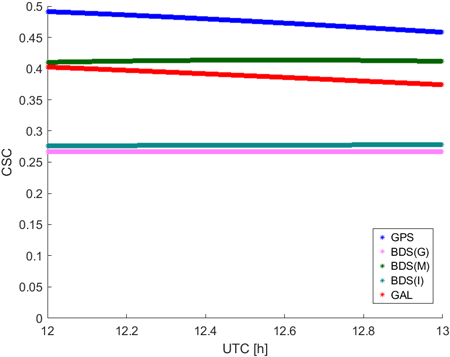
Fig. 3. Constellation-Specific Coefficient (CSC) values calculated over a one-hour interval.
Fig. 3에서 BDS(G)는 BeiDou 위성 중 GEO 위성을, BDS(I)는 IGSO 위성을 의미하며, CSC는 위성군 별 조정 계수를 의미한다. 각 위성군으로 G13, E13, C01 (GEO), C25 (MEO) 및 C38 (IGSO)를 선정하였다. GPS 위성의 CSC가 가장 높으며, 그 다음으로 BeiDou의 MEO 위성과 Galileo 위성이 높은 CSC를 갖는다. BeiDou의 IGSO 위성은 다소 낮은 CSC를 가지며, BeiDou의 GEO 위성이 가장 낮은 CSC를 가진다.
장에서 언급된 고도각 및 SNR 기반 가중값 모델들을 결합하면 Eq. (4)와 같다.
$$W_0 = \sin(E) + \frac{S}{60}$$
Eq. (4)에서는 고도각, SNR에 의해 각각 최대 1까지 가중값이 계산되므로, 이론적인 전체 가중값은 최대 2까지 계산된다. 그러나 본 연구에서는 가중값의 해석을 보다 직관적으로 할 수 있도록, 위 모델에 CSC를 곱하여 가중값 범위를 0과 1 사이로 제한하였다. 3.1절에서 언급한 바와 같이, 위성과의 거리에 따라 CSC는 0과 0.5 사이의 값을 가지며, 위성군 별 특성을 반영할 수 있다. 이를 적용한 최종 가중값 모델은 Eq. (5)와 같다.
$$W_1 = CSC \cdot \left( \sin(E) + \frac{S}{60} \right)$$
Eq. (5)에 따라 위성 유형 및 거리, 고도, SNR을 모두 반영한 통합 가중값을 부여할 수 있으며, Fig. 4는 CSC가 고정되었을 때, 고도각 및 SNR에 따른 가중값 변화를 나타낸다.
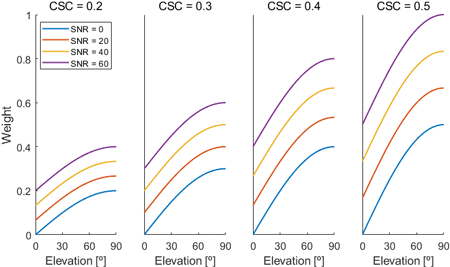
Fig. 4. Variation in weight according to elevation, SNR and CSC.
Fig. 4에서 CSC가 0.2로 작은 경우에는 고도각이 증가하고 SNR 값이 높아져도 최대 가중값은 약 0.4로 계산되지만, CSC가 0.5로 큰 경우에는 고도각과 SNR 값이 증가함에 따라 최대 가중값이 1로 계산된다. 이에 따라 위성의 고도각이 높고 신호 품질이 우수하며 MEO 궤도에 위치한 위성은 1에 가까운 높은 가중값을 갖게 되고, 반대로 고도 각이 낮고 신호 품질이 불량하며 GEO 궤도에 위치한 위성은 상대적으로 낮은 가중값을 갖게 된다. 이러한 방식은 위성의 물리적 위치에 기반한 거리, 위성 고도각 및 SNR을 모두 반영함으로써, 다중 GNSS 측위 정확도를 향상시키기 위한 가중값 모델로 활용될 수 있다.
이번 장에서는 위성군별 특성을 고려하지 않은 경우와 본 연구에서 제안한 위성별 차등 가중값을 적용한 경우의 측위 결과를 비교한다. 4.1절에서는 측위에 사용한 데이터들을 정의하고, 취득 방법 및 측위 기법을 기술한다. 4.2절에서는 산출된 측위 결과를 비교하고, 분석한다.
이 연구에서는 서울특별시 금천구에 위치한 대성디폴리스 지식산업센터의 옥상에 설치된 (주)피피솔 기준국 PPHQ의 데이터를 2025년 4월 20일(DOY 110)에, 정오부터 자정까지 1초 간격으로 총 12시간 동안 수집하였다. PPHQ 기준국은 30층 높이 건물의 옥상에 설치되어 있기 때문에 신호 차폐 요소가 없는 개활지 환경이다.
또한, 최소 제곱법을 활용한 코드 의사거리 기반 정밀 단독 측위 결과를 분석하였는데, 이 때 국토지리정보원에서 제공하는 State Space Representation (SSR) 보정정보를 이용하여 위성 궤도 및 시계오차를 보정하였다. 전리층 및 대류권 지연 오차 또한 SSR 보정 정보에서 제공하는 지연 오차 값을 수신기의 위도 및 경도에 맞게 보간하여 보정하였다. 측위 알고리즘에 기반이 된 코드 의사거리 관측 방정식은 Eq. (6)과 같으며, 측위에 사용된 위성 수는 Fig. 5에 나타낸다.
$$P = \rho + c (\delta t_r – \delta t^s) + \delta I + \delta T + MP + \varepsilon$$
여기서 $\rho$는 위성과 수신기 간 기선 거리이고, $\delta t_r$, $\delta t^s$는 각각 수신기 시계 오차와 위성 시계 오차이다. $\delta I$, $\delta T$는 각각 전리층 지연 오차와 대류권 지연 오차이다. $MP$는 다중경로 오차를 의미하며, 는 관측 잡음을 나타낸다. Fig. 5에서 볼 수 있듯이 BeiDou의 GEO 위성은 3~5개, IGSO 위성은 6~10개의 위성이 사용되었고, MEO 위성은 5~12개의 위성이 사용되었다. 또한 GPS는 8~13개의 위성이, Galileo는 7~13개의 위성이 사용되었다.
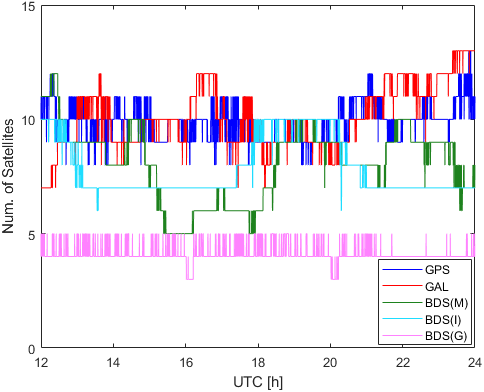
Fig. 5. Visible satellites at PPHQ reference station on 20 April 2025.
측위 결과 분석을 위하여 두 가지 형태의 시각화를 수행하였다. 먼저, Fig. 6에 동서와 남북 방향 오차 성분을 수평오차 그래프로 나타내어 측위 오차의 분포 및 바이어스를 파악하였으며, Fig. 7에 수직 오차 시계열 그래프를 나타내어 측위 오차의 변화 및 급격한 증가 여부를 분석하였다. Figs. 6과 7에 빨간색으로 나타낸 Case 0이 고도각 및 SNR만 고려한 Eq. (4)의 가중값 모델 적용 결과이며, 파란색으로 나타낸 Case 1이 위성과의 거리, 고도각 및 SNR을 모두 고려한 Eq. (5)의 가중값 모델 적용 결과이다. 성능 평가의 지표로 Root Mean Square Error (RMSE)를 사용하여 정확도 향상률과 함께 Table 1에 정리하였다.
Table 1. Horizontal, vertical, and 3D RMSE of Case 0 and Case 1, and accuracy improvement rate.
| Time (UTC+) | Case 0 (RMSE [cm]) | Case 1 (RMSE [cm]) | Improvement rate (%) | ||||
|---|---|---|---|---|---|---|---|
| H | v | 3d | h | v | 3d | ||
| 12:00 | 22.2 | 33.5 | 40.2 | 22.2 | 32.8 | 39.6 | 1.5 |
| 13:00 | 20.3 | 32.7 | 38.4 | 19.8 | 31.5 | 37.2 | 3.1 |
| 14:00 | 31.9 | 31.8 | 45.0 | 32.4 | 31.7 | 45.3 | -0.7 |
| 15:00 | 52.2 | 35.3 | 63.0 | 54.4 | 32.9 | 63.6 | -1.0 |
| 16:00 | 54.3 | 35.1 | 64.7 | 57.2 | 31.9 | 65.5 | -1.2 |
| 17:00 | 46.3 | 61.5 | 77.0 | 50.2 | 61.4 | 79.4 | -3.1 |
| 18:00 | 25.0 | 47.6 | 53.8 | 23.9 | 43.3 | 49.5 | 8.0 |
| 19:00 | 18.7 | 30.6 | 35.9 | 18.1 | 30.4 | 34.8 | 3.1 |
| 20:00 | 18.1 | 38.3 | 42.4 | 18.7 | 34.4 | 39.1 | 7.8 |
| 21:00 | 25.0 | 61.9 | 66.7 | 19.3 | 60.3 | 63.4 | 4.9 |
| 22:00 | 35.0 | 52.6 | 63.2 | 31.3 | 47.8 | 57.1 | 9.7 |
| 23:00 | 30.8 | 31.4 | 43.9 | 29.7 | 29.5 | 41.9 | 4.6 |
Fig. 6은 Case 0과 Case 1의 수평오차를 비교한 결과이다. Case 0, Case 1 모두 SSR 적용으로 안정적인 서브 미터 수준의 측위가 가능하다. 그림에서 볼 수 있듯이, 대부분 시간대에서 유사한 결과를 보이나, 13시 및 15시부터 17시의 경우처럼 동서와 남북 방향으로 바이어스가 있는 상황에서는 위성별 차등 가중값 모델을 적용했을 때 약간의 바이어스 저감 효과가 있는 것이 확인된다.
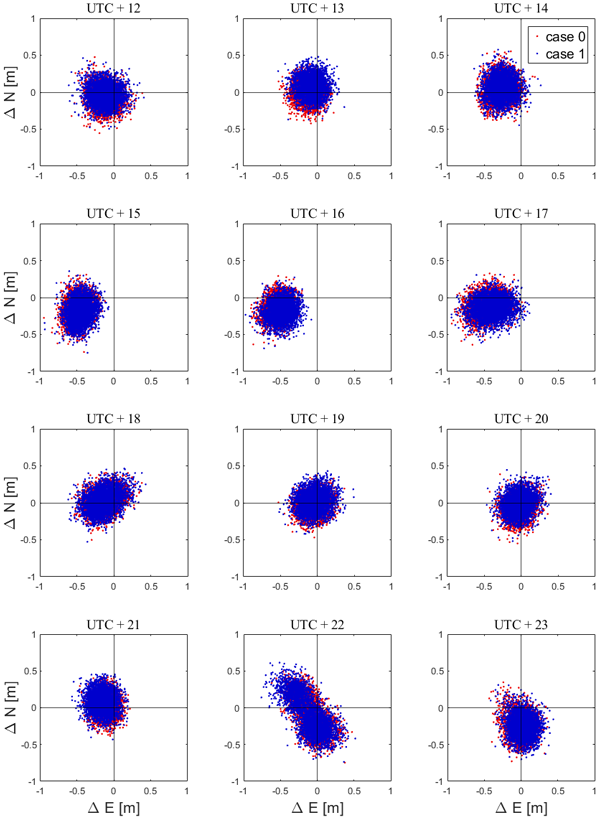
Fig. 6. Horizontal positioning error of relative positioning for Case 0 using elevation and SNR, and Case 1 with additional range-based weighting.
Fig. 7은 수직 오차를 시계열로 나타낸 결과이다. 22시의 경우, 위성별 차등 가중값 모델을 적용하지 않았을 때부터 바이어스가 크게 발생하는데, 위성별 차등 가중값 모델을 적용하면 정확도는 향상되지만 바이어스는 크게 줄어들지 않는 것이 확인된다. 또한, 대부분의 시간대에서 위성별 차등 가중값 모델을 적용한 경우에 정확도가 향상됨을 확인할 수 있다.
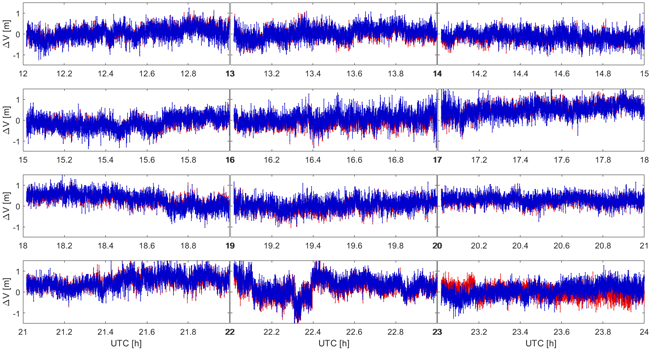
Fig. 7. Vertical positioning error of relative positioning for Case 0 (red) using elevation and SNR, and Case 1 (blue) with additional range-based weighting.
Table 1을 보면, 위성별 차등 가중값 모델을 적용한 Case 1의 경우, 대부분의 시간대에서 측위 정확도가 향상된다. 14시에서 17시에는 측위 정확도가 다소 낮아지는 경향이 있지만, 감소 정도가 크지 않고 Case 0과 유사한 결과를 보인다. 반면, 다른 시간대에서는 모두 정확도가 향상되는 것을 확인할 수 있으며, 22시의 경우 최대 9.7%까지 향상된다. 이는 위성군별 차등 가중값 모델을 적용하면 보다 정확한 위치 추정이 가능함을 보여준다. 한 시간 단위로 측위할 때 평균적으로 3.1% 만큼 정확도가 향상되며, 정확도가 감소한 시간대를 제외하면 향상 정도는 평균적으로 5.3%까지 증가한다. 또한 향상률의 표준편차는 4.1%로 과도하게 크지 않은 수준이다. 이는 시간대에 따른 측위 정확도 향상의 변동성이 작음을 의미하며, 다른 시간대 또는 날짜에서도 유사한 성능을 보일 것이 예상된다.
본 연구는 위성 고도각, SNR을 활용한 단독 가중값 모델의 한계를 설명하고, 위성과의 거리를 추가적으로 고려한 위성별 차등 가중값 모델을 제안하였다. 이를 검증하기 위해 PPHQ 상시 관측소 데이터를 기반으로 SSR 보정 정보를 활용하여 코드 의사거리 기반 정밀 단독 측위 결과를 분석하였다. 수평오차 그래프 및 시계열 그래프를 분석한 결과, 위성별 차등 가중값 모델을 적용한 경우에 전반적으로 측위 정확도를 향상시키는 경향을 보였다. 대부분 시간대에서 수평 및 수직 오차가 감소하였고, 최대 9.7%, 평균 3.1%의 정확도 향상을 보였다. 일부 시간대에서 정확도 저감이 있었으나, 감소폭이 작아 전체 경향에 큰 영향을 미치지 않았다. 또한, 표준편차가 4.1%로 낮게 나타났으므로 본 모델의 적용 가능성이 높다고 판단하였다.
본 연구는 기존에 활용되던 고도각과 SNR 기반의 단독 가중값 모델과 다르게, 위성군별 특징을 정량적으로 반영한 새로운 접근 방식을 제안하였다는 점에서 의의가 있다. 또한 위성군의 거리와 관측 신호 품질 요소를 통합적으로 고려한 가중값 모델이 다중 위성 정밀 단독 측위 성능 개선에 실질적인 영향을 줄 수 있음을 확인하였다. 향후 연구에서는 다양한 환경에서 추가적인 테스트를 수행하고 확장 칼만 필터 기반의 측위 결과를 분석하여 모델의 보편성을 검증할 필요가 있다.
본 연구는 2025년도 국토교통부의 재원으로 국토교통과학기술진흥원의 지원으로 수행된 연구임 (RS-2022-00141819, 초정밀 디지털 국토정보 획득을 위한 절대, 상대, 연속복합 측위 고도화 기술 개발).
All the authors have contributed to the presented work. H.S. conceived the research idea, designed the research, performed data analysis, and interpreted the results. H.S. also wrote the first draft of the manuscript. J.M. contributed to refining the research idea and collected the data for analysis. K.D. supervised this work and reviewed the manuscript.
The authors declare no conflict of interest.
Cai, C. & Gao, Y. 2007, Precise Point Positioning Using Combined GPS and GLONASS Observations, Journal of Global Positioning Systems, 6, 13-22.
Choi, B.-K., Cho, C.-H., Cho, J. H., & Lee, S. J. 2015a, Multi-GNSS Standard Point Positioning using GPS, GLONASS, BeiDou and QZSS Measurements Recorded at MKPO Reference Station in South Korea, Journal of Positioning, Navigation, and Timing, 4, 205-211. https://doi.org/10.11003/JPNT.2015.4.4.205
Choi, B.-K., Cho, C.-H., & Lee, S. J. 2015b, Precise Point Positioning using the BeiDou Navigation Satellite System in South Korea, Journal of Positioning, Navigation, and Timing, 4,73-77. https://doi.org/10.11003/JPNT.2015.4.2.073
Choi, B.-K., Cho, C.-H., & Lee, S. J. 2017a, Multi-GNSS Kinematic Precise Point Positioning: Some Results in South Korea, Journal of Positioning, Navigation, and Timing, 6, 35-41. https://doi.org/10.11003/JPNT.2017.6.1.35
Choi, B.-K., Yoon, H. S., & Lee, S. J. 2017b, Positioning Precision Improvement of Multi-GNSS Kinematic PPP Using WMN Method, Journal of Positioning, Navigation, and Timing, 6, 205-210. https://doi.org/10.11003/JPNT.2017.6.4.205
Joseph, A. 2010, Measuring GNSS Signal Strength, GNSS Solutions, available from: https://insidegnss.com/wp-content/uploads/2018/01/novdec10-Solutions.pdf
Kazmierski, K., Hadas, T., & Sośnica, K. 2018, Weighting of Multi-GNSS Observations in Real-Time Precise Point Positioning, Remote Sens., 10, 84. https://doi.org/10.3390/rs10010084
Kim, H.-I. 2015, Improvement of the real-time positioning accuracy in urban canyons through development of a new weight model based on GNSS signal strength, PhD Thesis, Inha University.
Li, X., Zhang, X., & Guo, F. 2009, Study on Precise Point Positioning Based on Combined GPS and GLONASS, Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, September 22-25, 2009, pp.2449-2459. https://www.ion.org/publications/abstract.cfm?articleID=8658
Li, X, Zhang, X., Ren, X., Fritsche, M., Wickert, J., et al. 2015, Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou, Sci. Rep., 5, 8328. https://doi.org/10.1038/srep08328
Park, B.-G. & Park, K.-D. 2024, Analysis of Double-Differenced Code-Pseudorange Noise Characteristics of GNSS Receiver Combinations using Zero-Baseline Test, Journal of Positioning, Navigation, and Timing, 13, 245-256. https://doi.org/10.11003/JPNT.2024.13.3.245
Tan, B., Yuan, Y., Wen, M., Ning, Y., & Liu, X. 2016, Initial Results of the Precise Orbit Determination for the New-Generation BeiDou Satellites (BeiDou-3) Based on the iGMAS Network, International Journal of GeoInformation, 5, 196-208. https://doi.org/10.3390/ijgi5110196