Department of Radio and Information Communication Engineering, Chungnam National University, Daejeon 34134, Korea
†Corresponding Author: Jae Min Ahn, E-mail: jmahn@cnu.ac.kr
Citation: Ha, E.J., Shin, J.H., & Ahn, J.M. 2025, Design of GNSS PRN Code Families Based on Truncated Gold Codes with Varying LFSR Orders, Journal of Positioning, Navigation, and Timing, 14, 167-171.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 June, Volume 14, Issue 2, pages 167-171. https://doi.org/10.11003/JPNT.2025.14.2.167
Received on May 21, 2025, Revised on May 29, 2025, Accepted on Jun 10, 2025, Published on Jun 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This paper presents the selection and analysis of PRN code groups with superior autocorrelation and cross-correlation properties based on truncated Gold codes for application in satellite navigation systems. Gold codes were generated by varying the order of the Linear Feedback Shift Register (LFSR) while maintaining a constant code length. The code groups were then selected by applying balance properties and correlation criteria. The number of codes satisfying the maximum even autocorrelation power of −28 dB, maximum odd autocorrelation power of −27.5 dB, and cross-correlation maximum powers of −26.4 dB and −25 dB were compared. The results indicate that, under a fixed code length, increasing the LFSR order tends to yield a greater number of codes that meet the cross-correlation criteria. Increasing the LFSR order is therefore expected to effectively enhance cross-correlation performance.
PRN, GNSS, Gold code, correlation
Global Navigation Satellite System (GNSS)은 직접 확산 기반의 코드 분할 다중접속 기술을 주요 신호 생성 방식으로 채택하고 있다. Code Division Multiple Access (CDMA)를 채용하고 있는 GNSS은 위성 신호 간 구분을 위하여 서로 다른 Pseudo Random Noise (PRN) 코드를 사용하며, 위성 간 간섭을 최소화할 수 있도록 PRN 코드군을 구성한다.
위성항법 측위 서비스를 위한 PRN 코드는 신호의 획득 및 추적을 통해 위성 송신기와 지상 수신기 간의 거리 측정에 활용되므로 서로 다른 코드 간의 최대 상호상관 전력 값 최소화하는 것이 목적이다. 이를 위해 상관 특성이 우수한 코드들이 사용되며, 대표적으로 1023의 배수 중 적절한 길이로 구성된 골드코드, 웨일코드, 카사미코드 등이 있다. 이 중, 골드코드는 Linear Feedback Shift Register (LFSR) 구조를 기반으로 하여 비교적 구현이 간단하므로 여러 위성 신호에서 채택하고 있다 (Jin et al. 2012, Kim et al. 2020).
GPS의 L1 대역에서 송신하는 Coarse/Acquisition (C/A) 코드는 주기 210-1의 골드코드를 기반으로 PRN 코드군을 구성하고 있다. 그러나 Global Positioning System (GPS) 이후에 등장한 GNSS들은 신호 획득 성능의 개선을 목적으로 PRN 코드의 주기를 더 길게 설계하는 추세이다. 이러한 시스템에서는 기존 L1 C/A코드 대비 10배 증가한 10230칩 길이의 PRN 코드를 사용하고 있다 (Cabinet Office 2025, China Satellite Navigation Office 2019, European Union 2023). 이 경우 주기가 2n-1의 형태를 따르지 않기 때문에 골드코드를 그대로 사용할 수 없다는 문제가 발생한다.
골드코드는 주기 2n-1에서 우수한 상관 특성을 나타낸다 (Sarwate & Pursley 1980). 그러나 10230칩 길이의 PRN 코드 생성할 경우, 이러한 특성이 유지되지 않아 랜덤 이진코드와 유사한 상호상관을 보인다. 따라서 코드의 주기가 2n-1과 다른 경우 해당 주기에서 좋은 상관 특성을 보이는 코드의 선별 과정이 필요하다. 실제로 Galileo E5는 주기 16383의 골드코드를 생성한 후 10230칩의 길이로 잘라 상관 특성이 양호한 코드를 선별하여 코드를 구성하고 있다 (European Union 2023).
기존 연구에서는 18차 LFSR과 14차 LFSR을 이용하여 상호상관 특성이 우수한 PRN 코드군을 생성하는 방법을 제시하였다 (Kim et al. 2019, Shin & Ahn 2024). 상관 특성 개선을 위해, 본 논문에서는 기존 연구를 확장하여 LFSR 차수 14, 15, 17, 18을 고려한 코드군을 생성하고, 각 차수별로 상호상관 특성이 우수한 코드를 선별하였다. 또한, 차수별 확보 가능한 후보 코드 수를 분석하고, 각 코드 차수와 코드군 내 상호상관 특성 간의 관계를 제시하였다.
서론에 이어 2장에서는 PRN 코드군 생성 방법에 대해 서술한다. 3장에서는 PRN 코드군 생성 결과 및 분석에 대해 서술하고 4장에서는 결론을 맺는다.
잘린 골드코드는 두 개의 n-차 LFSR로부터 생성된 선형 수열 G1, G2를 exclusive-or하여 얻은 골드코드를 일정 길이로 잘라서 구성한다. 본 논문에서는 n = 14, 15, 17, 18에 대한 생성 다항식을 사용하였으며 코드의 주기는 2n-1로 결정된다. 이때 n = 16의 경우에는 preferred pair가 존재하지 않아 골드코드 생성을 위한 차수로 사용할 수 없어 제외하였다. 각 차수별로 사용된 생성 다항식은 Table 1에 정리되어 있으며, 전체 코드 생성 구조는 Fig. 1에 나타내었다 (Partow 2024).
Table 1. Primitive polynomials for G1 and G2.
| LFSR order | G1 primitive polynomial | G2 primitive polynomial |
|---|---|---|
| 14 | x14 + x10 + x6 + x + 1 | x14 + x10 + x9 + x7 + x6 + x4 + x3 + x + 1 |
| 15 | x15 + x + 1 | x14 + x7 + x6 + x3 + x2 + x + 1 |
| 17 | x17 + x3 + 1 | x17 + x3 + x2 + x + 1 |
| 18 | x18 + x11 + 1 | x18 + x13 + x11 + x8 + 1 |
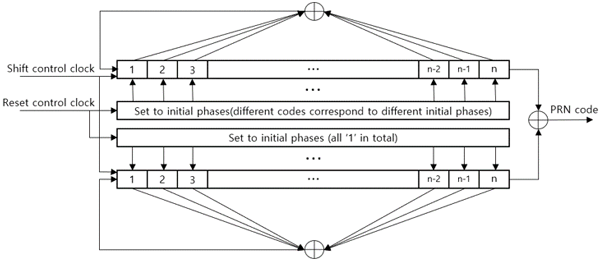
Fig. 1. The generator of PRN code.
G1과 G2의 modulo-2 덧셈으로 생성된 골드코드는 10230칩으로 잘라서 사용한다. G1의 초기 값은 위성 신호에 따라 다르게 결정하고, G2는 모든 경우에 대해 ‘1’로 초기화하여 사용한다. Fig. 1의 생성기로부터 2n-1개의 잘린 코드군을 얻을 수 있다.
골드코드는 주기가 2n-1일 때 최적 상호상관 전력 특성을 나타낸다. 주기 10230의 PRN 코드를 구성하기 위해 2n-1 주기를 갖는 골드코드를 생성한 후 잘라서 코드군을 구성한다. 이 경우, 전체 주기를 만족하지 않으므로 10230 길이 내에서 상관 특성이 우수한 코드를 선별하는 과정이 추가적으로 필요하다.
코드 선별 절차는 다음과 같다. Fig. 1로부터 생성한 2n+1개의 잘린 골드코드군에서 균형 특성을 만족하는 시퀀스를 우선적으로 선별한다. 균형 특성은 1의 개수가 0의 개수보다 하나 더 많은 것을 의미하지만, 잘린 코드의 주기가 짝수인 점을 고려하여 1의 개수와 0의 개수가 동일한 경우를 균형 특성을 만족하는 것으로 하였다. 선별된 코드에 대해 짝수, 홀수 자기상관의 최대값을 계산하고 자기상관 부엽 값을 제한하여 두 조건에 모두 만족하는 코드를 선택한다. Eqs. (1-2)는 짝수, 홀수 자기상관 부엽의 최대 전력을 계산하는 수식을 나타낸 것이다 (Kim et al. 2019).
$$\begin{align}
R_{e,i}[\tau] &= \sum_{n=0}^{L-1-\tau} c_i[n] c_i[n+\tau] + \sum_{n=L-\tau}^{L-1} c_i[n] c_i[n+\tau-L], \quad n = 0, 1, \cdots, L-1 \notag \\
R_{\text{max},e,i} &= 10 \log_{10} \left( \frac{\max_{\tau \ne 0} \left\{ \left| R_{e,i}[\tau] \right|^2 \right\}}{L^2} \right)
\end{align}$$
$$\begin{align}
R_{o,i}[\tau] &= \sum_{n=0}^{L-1-\tau} c_i[n] c_i[n+\tau] – \sum_{n=L-\tau}^{L-1} c_i[n] c_i[n+\tau-L], \quad n = 0, 1, \cdots, L-1 \notag \\
R_{\text{max},o,i} &= 10 \log_{10} \left( \frac{\max_{\tau \ne 0} \left\{ \left| R_{o,i}[\tau] \right|^2 \right\}}{L^2} \right)
\end{align}$$
여기서 ci [n]는 균형 특성을 만족하는 i-번째 잘린 골드코드이며, 코드주기 L은 10230의 값을 갖는다. $\tau$는 $0 \le \tau < L$ 범위의 정수 값을 가지는 코드 지연을 의미한다. $R_{e,i}[\tau]$, $R_{o,i}[\tau]$는 각각 짝수, 홀수 자기상관이고, $R_{max,e,i}$, $R_{max,o,i}$는 해당 자기상관 부엽의 정규화된 최대 전력이다.
다음으로, 자기상관 기준을 만족하는 코드들을 대상으로 상호상관 분석을 수행하고 짝수 및 홀수 지연에 대한 상호상관 전력이 기준을 초과하지 않는 경우에만 코드군에 포함시킨다. Eqs. (3-4)는 각각 짝수, 홀수 상호상관 최대 전력을 계산하는 수식을 나타낸다 (Kim et al. 2019).
$$\begin{align}
R_{e,kl}[\tau] &= \sum_{n=0}^{L-1-\tau} c_k[n] c_l[n+\tau] + \sum_{n=L-\tau}^{L-1} c_k[n] c_l[n+\tau-L], \quad n = 0, 1, \cdots, L-1 \notag \\
R_{\text{max},e,kl} &= 10 \log_{10} \left( \frac{\max_{\tau \ne 0} \left\{ \left| R_{e,kl}[\tau] \right|^2 \right\}}{L^2} \right)
\end{align}$$
$$\begin{align}
R_{o,kl}[\tau] &= \sum_{n=0}^{L-1-\tau} c_k[n] c_l[n+\tau] – \sum_{n=L-\tau}^{L-1} c_k[n] c_l[n+\tau-L], \quad n = 0, 1, \cdots, L-1 \notag \\
R_{\text{max},o,kl} &= 10 \log_{10} \left( \frac{\max_{\tau \ne 0} \left\{ \left| R_{o,kl}[\tau] \right|^2 \right\}}{L^2} \right)
\end{align}$$
여기서 $R_{e,kl}[\tau]$, $R_{o,kl}[\tau]$는 k-번째 코드와 l-번째 코드 간의 짝수, 홀수 상호상관을 의미하며, $R_{max,e,kl}$, $R_{max,o,kl}$는 해당 상호상관의 정규화된 최대 전력이다.
LFSR의 차수를 변화시키고 동일한 길이로 잘린 골드코드로 구성된 코드군에 대해 상호상관 전력 기준을 적용하여 코드 선별을 수행하였다. 이후 각 차수에 대해 동일한 조건 하에서 선택 가능한 코드 개수를 비교함으로써, 코드 차수가 상호상관 특성 및 코드군 구성에 미치는 영향을 분석하였다.
코드 선별은 다음과 같은 단계로 이루어진다. 먼저, 균형 특성을 만족하는 시퀀스를 선별하였다. 다음으로, 자기상관 부엽 전력의 제한 기준을 각각 짝수는 -28 dB, 홀수는 -27.5 dB로 설정하여 조건을 만족하는 코드를 선택하였다. 마지막으로, 상호상관 전력의 제한 값을 -26.4 dB로 적용하여 코드군을 구성하고 동일한 코드군에 -25 dB 기준을 추가로 적용하여 코드 수의 변화를 확인하였다. 해당 기준은 모든 차수에 동일하게 적용되었으며 차수별로 선별된 코드 수의 차이를 비교하였다.
Table 2는 각 LFSR 차수에 대해 생성 가능한 전체 코드 수와 자기상관 기준을 만족하는 코드 수를 정리한 것이다. 자기상관 부엽의 최대 전력 기준은 각각 -28 dB, -27.5 dB로 설정되었으며, 상호상관 전력 제한은 적용하지 않았다. 차수가 증가함에 따라 자기상관 조건을 만족하는 코드 수는 증가하는 경향을 보인다.
Table 2. Number of codes satisfying the auto-correlation criterion for each LFSR degree.
| LFSR order | Total codes | Codes passing autocorrelation criterion |
|---|---|---|
| 14 | 16,385 | 102 |
| 15 | 32,769 | 203 |
| 17 | 131,073 | 685 |
| 18 | 262,145 | 1,439 |
자기상관 기준을 만족한 코드에 대해 짝수 및 홀수 상호상관의 최대 전력이 모두 -24.5 dB 이하인 경우와 모두 -25 dB 이하인 경우를 기준으로 코드군을 구성하고 기준별로 선별된 코드 수를 비교하였다. 이때 사용된 -26.4 dB와 -25 dB는 각각 GPS L5와 Galileo E5에서 사용하는 코드 간 정규화된 상호상관 최대 전력을 기준으로 설정된 값이다 (Mongredien et al. 2006). Table 3은 각 LFSR 차수에 대해 이 기준들을 만족한 코드의 수를 정리한 것이며, Figs. 2-9는 LFSR 차수 별 상호상관 전력 제한 기준을 만족하는 코드들 간의 상호상관 전력의 분포를 나타낸다.
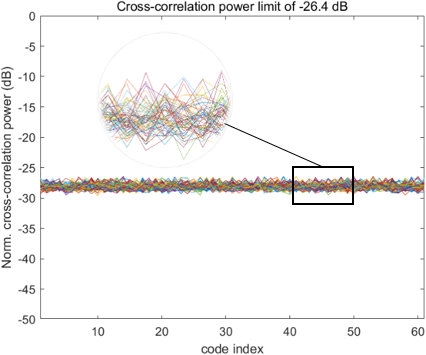
Fig. 2. Cross-correlation power limit of -26.4 dB for 14-stage LFSR.
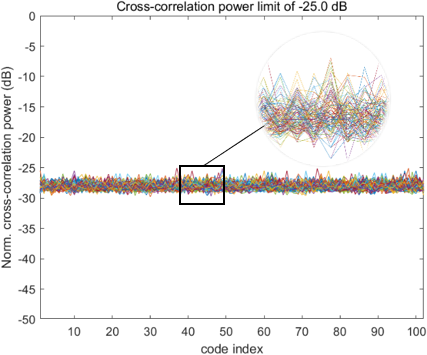
Fig. 3. Cross-correlation power limit of -25 dB for 14-stage LFSR.
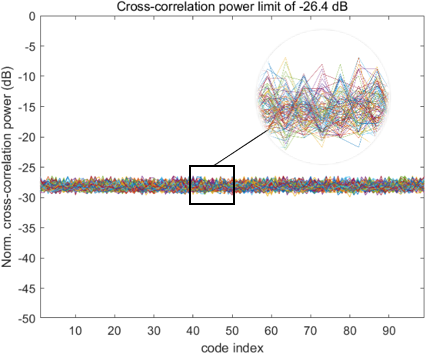
Fig. 4. Cross-correlation power limit of -26.4 dB for 15-stage LFSR.
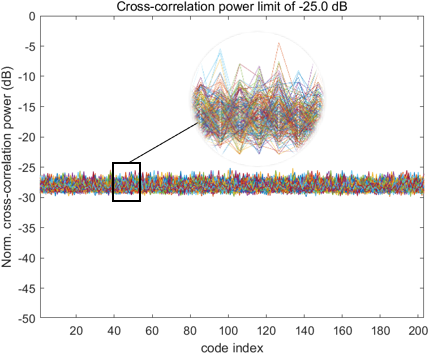
Fig. 5. Cross-correlation power limit of -25 dB for 15-stage LFSR.
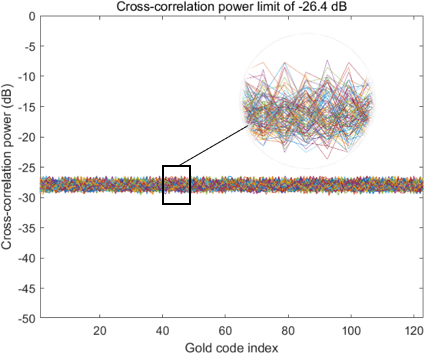
Fig. 6. Cross-correlation power limit of -26.4 dB for 17-stage LFSR.
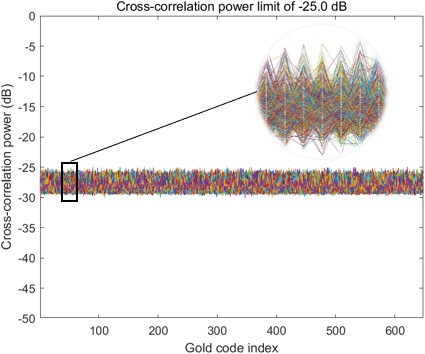
Fig. 7. Cross-correlation power limit of -25 dB for 17-stage LFSR.
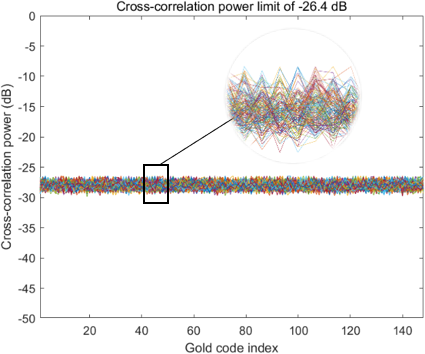
Fig. 8. Cross-correlation power limit of -26.4 dB for 18-stage LFSR.
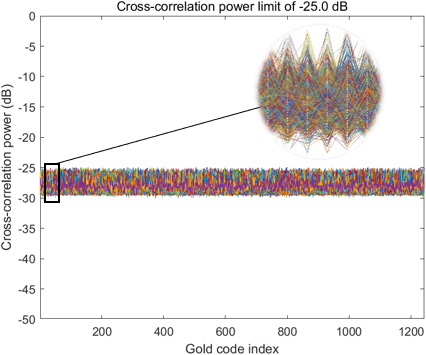
Fig. 9. Cross-correlation power limit of -25 dB for 18-stage LFSR.
Table 3. Number of codes satisfying the cross-correlation criterion for each LFSR degree.
| LFSR order | Code passing the -26.4 dB criterion | Code passing the -25 dB criterion |
|---|---|---|
| 14 | 61 | 102 |
| 15 | 99 | 203 |
| 17 | 123 | 648 |
| 18 | 148 | 1,243 |
전체적으로 LFSR 차수가 증가함에 따라 두 기준 모두에서 선별된 코드 수가 증가하는 경향을 보였다. 14차에서는 각각 61개와 102개, 18차에서는 148개와 1243개의 코드가 기준을 만족하였다. 이는 동일한 코드 길이로 잘랐을 때 LFSR 차수가 클수록 코드 간 상호상관 특성이 개선됨을 보여준다. 또한 제한 기준을 완화할수록 확보 가능한 코드 수가 증가하는 것을 확인할 수 있다.
본 논문은 주기 10230의 PRN 코드를 구성하기 위해 잘린 골드코드를 기반으로 하여 코드군 생성 및 선별 과정을 수행하였다. LFSR 차수를 14. 15, 17, 18로 설정하여 골드코드를 생성하고 자기상관, 상호상관 특성이 우수한 코드들을 선별하였다.
분석 결과, 동일한 코드 길이에서 LFSR 차수가 증가할수록 상호상관 기준을 만족하는 코드 수가 증가하는 경향을 보였다. 따라서 코드군 내에서 상호상관 특성을 개선하기 위해서는 LFSR의 차수를 증가시키는 것이 효과적임을 확인할 수 있었다.
Conceptualization, J. Shin and J. Ahn; methodology, E. Ha, J. Shin, and J. Ahn; software, J. Shin; validation, E. Ha and J. Shin; formal analysis, E. Ha and J. Shin; investigation, E. Ha and J. Shin; writing—original draft preparation, E. Ha; writing—review and editing, J. Ahn; supervision, J. Ahn.
The authors declare no conflict of interest.
Cabinet Office 2025, Quasi-Zenith Satellite System Interface Specification, Centimeter Level Augmentation Service (IS-QZSS-L6-006)
China Satellite Navigation Office 2019, BeiDou Navigation Satellite System Open Service, BDS OS SIS ICD Version 3.0
European Union 2023, European GNSS(Galileo) Open Service, OS SIS ICD issue 2.1
Jin, M.-H., Choi, H.-H., Kim, K.-J., Park, C., Ahn, J.-M., et al. 2012, The Design Method of GNSS Signal Using the Analysis Result of Receiver Performance, JKICS, 37, 502-511.
Kim, G., Song, H.-Y., Lim, D.-W., & Ahn, J.-M. 2020, Some Generation Methods of Truncated Gold Codes for GNSS, JKICS, 45, 867-874. https://doi.org/10.7840/kics.2020.45.5.867
Kim, S.-T., Kim, K.-J., Song, K.-W., & Ahn, J.-M. 2019, Selection Technique of Maximum Correlation Power Limited Gold Code Set of Limited Length, JKICS, 44, 629-636. https://doi.org/10.7840/kics.2019.44.4.629
Mongredien, C., Lachapelle, G., & Cannon, M. E. 2006, Testing GPS L5 Acquisition and Tracking Algorithms Using a Hardware Simulator, in Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), Fort Worth, TX, 26-29 Sep 2006, pp.2901-2913. https://www.ion.org/publications/abstract.cfm?articleID=6811
Partow, A. 2024, [Internet], available from: https://www.partow.net/programming/polynomials/index.html#deg02G2
Sarwate, D. V. & Pursley, M. B. 1980, Cross-correlation properties of pseudorandom and related sequences, Proceedings of the IEEE, 68, 593-619. https://doi.org/10.1109/PROC.1980.11697
Shin, J. H. & Ahn, J. M. 2024, Generation of PRN Code Family for GNSS Signals Using Truncated Gold Codes, Proc. of the 2024 Conference on Institute of Positioning, Navigation and Timing (IPNT), Jeju, Korea, 6-8 Nov 2024, pp.329-332. https://ipnt.or.kr/2024proc/145