Satellite Navigation R&D Division, Korea Aerospace Research Institute, Daejeon 34133, Korea
†Corresponding Author: Heesung Kim, E-mail: hskim15@kari.re.kr
Citation: Kim, H., & Son, M., 2024, Estimation of the Relative GPS/Galileo Satellite and Receiver IFBs using a Kalman Filter in a Regional Receiver Network, Journal of Positioning, Navigation, and Timing, 13, 309-317.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2024 September, Volume 13, Issue 3, pages 309-317. https://doi.org/10.11003/JPNT.2024.13.3.309
Received on Aug 15, 2024, Revised on Aug 28, 2024, Accepted on Aug 30, 2024, Published on Sep 15, 2024.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Satellite and receiver Inter-Frequency Biases (IFBs) should be estimated or calibrated by pre-defined values for generating precise navigation messages and augmentation data in satellite navigation systems or the augmentation system. In this paper, a Kalman filter is designed and implemented to estimate the ionospheric delay and satellite/receiver IFBs using a regional receiver network. First, an ionospheric model and its filter parameter is defined based on previous studies. Second, a measurement model for estimating the relative satellite/receiver IFBs without any constraints is proposed. Third, a procedure for ensuring the continuity of estimation is proposed in this paper. To verify the performance of the designed filter, six Continuously Operating Reference Stations (CORSs) are selected. Finally, the stability and accuracy of satellite/receiver IFB estimation are analyzed.
IFB, relative, GPS, Galileo, Kalman filter
다중 주파수를 사용하는 Global Navigation Satellite System (GNSS) 수신기의 측정데이터는 위성과 수신기 주파수간 편이(Inter-Frequency Bias; IFB)의 영향을 받는다 (Montenbruck et al. 2014). IFB는 위성과 수신기의 하드웨어 설계에 의해 주파수 및 코드 별 신호지연이 다르게 발생함에 따라 발생한다. GPS의 경우에 L1 P(Y)와 L2 P(Y) 코드 사이에 약 8.3 ns (2.5 m) L1 C/A 코드와 L2 P(Y) 코드 사이에 약 10 ns (3.0 m)의 위성 IFB가 존재한다 (Montenbruck et al. 2014). 수신기 IFB는 수신기 제조사에 따라 서로 다른 값을 가지며, L1 C/A 코드와 L2 P(Y) 코드 사이에 20~40 ns (6~12 m) 정도의 값을 가진다 (Han 2018). 따라서, 위성과 수신기 IFB는 이중주파수 조합 측정데이터를 사용하는 응용분야에서 사전에 보정하거나 추정하여야 하는 필수 요소가 된다.
민간 사용자의 GNSS 다중주파수 활용을 위해 모든 GNSS 서비스 제공자는 항법메시지를 통해 위성 IFB를 사용자에게 제공한다 (Wang et al. 2019a). GPS의 경우 L1 P(Y)와 L2 P(Y) 코드에 대한 IFB를 TGD라는 변수를 통해 제공하며, L1 P(Y)와 L2C, L5I5, L5Q5 코드 사이의 IFB를 Inter-Satellite Correction이라는 변수를 통해 제공한다. Galileo의 경우에는 E1-E5a와 E1-E5b 코드 사이의 IFB를 BGD라는 변수를 통해 방송하고 있으며, BeiDou는 B1-B3와 B2-B3 코드 사이의 IFB를 TGD1과 TGD2를 통해 방송하고 있다. 이와 함께, International GNSS Service (IGS) 및 Multi-GNSS Experiment (MGEX)에서는 다중 GNSS/주파수에 대한 정밀 IFB 값을 제공하고 있다 (IGS 2024).
GPS 위성의 경우에는 Block IIR-M과 IIF 이후의 위성부터 Civil Navigation (CNAV) 메시지를 제공하고 있다. CNAV를 통해 방송하는 위성 IFB는 이전 Lagacy Navigation에서 제공하는 위성 IFB에 비해 정확도가 점차 향상되고 있으며, MGEX에서 제공하는 위성 IFB에 대해 수 ns 이내의 정밀도를 가지고 있다 (Tetewsky et al. 2009, Steigenberger et al. 2015, Wang et al. 2019a, 2019b). 따라서, GNSS 사용자는 MGEX 또는 항법메시지를 통해 제공하는 위성 IFB를 사용하여, 해당 오차의 영향을 완화하는 것이 가능하다.
반면, GNSS 서비스 제공자 또는 GNSS 보강서비스 제공자는 항법메시지의 생성이나 보강데이터의 생성을 위해 위성 및 수신기 IFB를 자체적으로 추정 및 감시하여야 한다. GNSS 보강시스템은 할당된 요구사항 및 설계에 따라 항법메시지에 포함되거나 오프라인 형태로 획득된 위성 IFB를 사용하는 것이 가능하며, 일부 GNSS 보강시스템의 경우에는 항법메시지에 포함된 위성 IFB와 함께 자체적으로 추정된 위성 IFB를 사용하여 보강데이터를 생성 및 감시하고 있다 (Walter et al. 2012, Sunehra 2016, Authié et al. 2017).
일반적으로 위성과 수신기 IFB를 추정하기 위해 GNSS 이중주파수의 Geometry-Free (GF) 조합 측정데이터를 사용하며, 전리층 지연 및 위성/수신기 IFB를 동시에 추정한다. GF 조합 측정데이터에서 위성과 수신기 IFB는 선형 조합으로 모델링되기 때문에 위성과 수신기 IFB를 분리 추정하는 것이 어렵다 (Schaer 1999). Ma & Maruyama (2003)는 위성과 수신기 IFB의 분리를 위해 수신기 IFB 중 하나를 0으로 설정한 뒤 장시간 데이터를 누적하여 Singular Value Decomposition 방식으로 위성 및 수신기 IFB를 추정하였다. Kim et al. (2012)은 위성과 수신기 IFB가 결합된 형태로 상태변수를 설정하여 장시간 데이터를 누적하여 추정한 뒤, 모든 위성 IFB의 합이 0이라는 조건을 사용하여 최종 위성 및 수신기 IFB를 추정하였다. Maheshwari et al. (2019)는 수신기 IFB 중 하나를 고정된 값이라 가정하여 Kalman 필터를 설계하였으며, Erdogan et al. (2017)는 측정데이터의 순차적인 처리를 위해 위성의 IFB 합이 0이라는 제약사항을 포함하여 Kalman 필터를 설계하였다.
Ma & Maruyama (2003)와 Kim et al. (2012)이 제안한 방법은 장시간 데이터를 누적하여 처리하는 방식이기 때문에 추정하고자 하는 상태변수의 개수에 비해 상대적으로 많은 상태변수와 측정데이터가 요구된다. Erdogan et al. (2017)와 Maheshwari et al. (2019)이 제안한 방법은 Kalman 필터를 사용한 순차적인 처리 방법이기 때문에 위에서 언급한 방법에 비해 상대적으로 적은 양의 측정데이터와 상태변수를 필요로 하고, 준실시간 전리층 지연 및 위성/수신기 IFB 추정할 수 있다는 장점을 가진다.
위성/수신기 IFB 분리 추정과 관련된 기존 연구는 기준 수신기 IFB를 임의의 값으로 설정하고 이에 대한 상대적인 위성/수신기 IFB를 추정하는 방식과 추정변수로 설정된 모든 위성의 IFB 값의 합이 0이라는 제약조건을 사용하는 방식으로 나눌 수 있다. 두 가지 방식 모두 상대적인 IFB 값을 추정한다는 공통점을 가지며, 효과적으로 위성/수신기 IFB를 분리할 수 있는 방식으로 알려져 있다. 다만, 위성이나 기준 수신기의 고장이나 가시성으로 인하여 발생가능한 소실(outage)에 대해서는 고려하고 있지 않다는 한계점을 가진다.
최근 국내에서는 지역 항법시스템인 Korean Positioning System (KPS)의 개발이 진행 중에 있으며, KPS와 다중 GNSS를 보강하기 위한 차세대 Korea Augmentation Satellite System (KASS)에 대한 연구가 요구되고 있다. KPS의 경우에는 지역적으로 수집된 데이터를 사용하여 추정된 위성 IFB를 사용자에게 제공하여야 하며, 차세대 KASS의 경우에는 GPS 뿐 아니라 다중 GNSS에 대한 수신기 및 위성 IFB 추정을 기반으로 하여 보강데이터를 생성 및 감시하여야 한다.
기존 연구는 위성과 수신기 IFB의 절대값을 추정하지 않고, 한기의 위성 또는 수신기 IFB에 대해 상대적인 IFB를 추정한다는 공통점을 가진다. 이에 본 연구에서는 기준이 되는 위성을 설정하여 상대적인 위성/수신기 IFB를 추정하기 위한 Kalman 필터를 설계한다. 이와 함께, 지역적인 수신기 네트워크로 구성되는 항법시스템 또는 보강시스템의 실 운영 환경에서 발생가능한 기준 위성의 소실 및 변화를 고려하여 추정의 연속성을 확보하기 위한 방안을 제안한다.
GPS/Galileo 코드 측정데이터는 Eq. (1)과 같이 모델링이 가능하다.
$$\tilde{\rho}^{j}_{r,s,na,k} = \rho^{j}_{r,k} + O^{j}_{r,s,k} + B^{j}_{r,s,k} – b^{j}_{s,k} + T^{j}_{r,k} + \alpha_{s,n} I^{j}_{S,r,k} + B_{HB,r,s,na} + B_{PCO,r,s,n} + b^{j}_{HB,s,na} + b^{j}_{PCO,s,n} + v^{j}_{r,s,na,k}$$
여기서, $\tilde{\rho}$는 코드 측정데이터, $\rho$는 위성과 수신기 사이의 거리, $O$는 위성궤도 오차에 의한 거리오차, $B$는 수신기 시계오차, $b$는 위성 시계오차, $T$는 대류층 지연, $I_S$는 경사 전리층 지연, $B_{HB}$는 수신기 하드웨어 바이어스, $B_{PCO}$는 수신기 안테나 위상 중심 편이에 의한 거리오차, $b_{HB}$는 위성 하드웨어 바이어스, $b_{PCO}$는 위성 안테나 위상 중심 편이에 의한 거리오차, 그리고 $v$는 측정오차를 의미한다. 첨자 j는 위성 번호, $r$은 수신기 번호, $s$는 위성군, $n$은 주파수 대역, $a$는 추적 모드 또는 채널, 그리고 $k$는 측정 시점을 의미한다. 마지막으로, $\alpha$는 위성군 $s$의 Ln 주파수에 대한 GPS L1 주파수의 비율에 제곱을 취한 값이며 Eq. (2)와 같다.
$$\alpha_{s,n} = \frac{(f_{G,1})^2}{(f_{s,n})^2}$$
여기서, $f$는 위성군 s의 n-번째 주파수 대역에서의 주파수에 해당하며, G는 GPS 지시자를 의미한다.
Eq. (1)에서 수신기/위성 안테나 위상 중심 편이는 각각의 하드웨어 바이어스에 포함되며, GPS와 Galileo 코드 측정데이터의 Geometry-Free (GF) 선형조합은 Eqs. (3, 4)와 같이 모델링이 가능하다.
$$\begin{align}
\tilde{\rho}^{j}_{r,G,1C2W,k} = & \ \tilde{\rho}^{j}_{r,G,1C,k} – \tilde{\rho}^{j}_{r,G,2W,k} \notag \\
= & \ (\alpha_{G,1C} – \alpha_{G,2W}) I^{j}_{S,r,k} + (B_{HB,r,G,1C} – B_{HB,r,G,2W}) \notag \\
& + (b^{j}_{HB,G,1C} – b^{j}_{HB,G,2W}) + (v^{j}_{r,G,1C,k} – v^{j}_{r,G,2W,k}) \notag \\
= & \ \alpha_{G,1C2W} I^{j}_{S,r,k} + B_{r,G,1C2W} + b^{j}_{G,1C2W} + v^{j}_{r,G,1C2W,k}
\end{align}$$
$$\begin{align}
\tilde{\rho}^{j}_{r,E,1X5X,k} = & \ \tilde{\rho}^{j}_{r,E,1X,k} – \tilde{\rho}^{j}_{r,E,5X,k} \notag \\
= & \ (\alpha_{E,1X} – \alpha_{E,5X}) I^{j}_{S,r,k} + (B_{HB,r,E,1X} – B_{HB,r,E,5X}) \notag \\
& + (b^{j}_{HB,E,1X} – b^{j}_{HB,E,5X}) + (v^{j}_{r,E,1X,k} – v^{j}_{r,E,5X,k}) \notag \\
= & \ \alpha_{E,1X5X} I^{j}_{S,r,k} + B_{r,E,1X5X} + b^{j}_{E,1X5X} + v^{j}_{r,E,1X5X,k}
\end{align}$$
여기서, G와 E는 각각 GPS와 Galileo 위성군에 대한 지시자를 의미한다. 1C/2W/1X/5X는 본 연구에서 사용하는 측정데이터의 주파수 대역 및 추적모드를 의미하며 RINEX Version 3.04에 제시된 표기법을 따른다 (IGS 2018). Eq. (3)은 j-번째 GPS 위성에 대한 C1C와 C2W 코드 측정데이터의 GF 선형조합 측정데이터이며, Eq. (4)는 j-번째 Galileo 위성에 대한 C1X와 C5X 코드 측정데이터의 GF 선형조합 측정데이터를 의미한다. Eqs. (3, 4)에서 $B_{r,G,1C2W}$과 $B_{r,E,1X5X}$는 각각 r-번째 수신기에서 GPS와 Galileo 측정데이터에 대한 수신기 IFB를 의미하며, $b^{j}_{G,1C2W}$과 $b^{j}_{E,1X5X}$는 j-번째 GPS와 Galileo 측정데이터에 대한 위성 IFB를 의미한다. Eqs. (3, 4)에서 전리층 지연은 Ionospheric Pierce Point (IPP)에서의 사상함수에 의해 Eq. (5)와 같이 모델링한다 (Schaer 1999).
$$I^{j}_{S,r,k} = F^{j}_{r,k} I^{j}_{V,r,k}$$
여기서, $I_V$는 수직 전리층 지연을 의미하며, $F$는 수신기 r에서 위성 j까지의 시선각 벡터와 전리층 단층(single layer) 사이의 교차 지점에서 수직 전리층 지연을 경사 전리층 지연으로 변환하기 위한 사상함수를 의미한다.
Eqs. (3, 4)에서 수직 전리층 지연, 위성 및 수신기 IFB는 선형조합으로 구성되기 때문에 각 위성/수신기 채널에 대해 개별적인 필터를 사용하여 상태변수를 추정하기 어렵다. 따라서 본 연구에서는 다수의 기준국 수신기로부터 수집된 측정데이터를 사용하여 전리층 지연과 위성/수신기 IFB를 추정하기 위한 필터를 설계한다.
전리층 지연을 모델링하기 위해 구면조화확장(Spherical Harmonics Expansion; SHE) 기법을 주로 사용하고 있다 (Schaer 1999, Choi et al. 2010, Yun et al. 2013). Maheshwari et al. (2019)는 삼각 내삽(triangular interpolation) 방식으로 전리층을 모델링하였으며, Erdogan et al. (2017)는 B-spline 방식으로 전리층을 모델링하였다. 이 중 SHE 방식은 차수에 따라 지구전역, 대륙, 그리고 지역 적인 모델링이 가능하며 (Wang et al. 2021), IGS Global Ionospheric Map의 생성을 위한 전리층 모델로 사용되고 있다 (Zhang & Zhao 2019). 이에, 이 논문에서는 SHE 방식을 사용하여 전리층을 Eq. (6)과 같이 모델링한다.
$$I^{j}_{V,r,k} = \sum_{n=0}^{2} \sum_{m=0}^{n} \left[ C_{nm} \cos(m \lambda^{j}_{ipp,r,k}) + S_{nm} \sin(m \lambda^{j}_{ipp,r,k}) \right] P_{nm} \left( \sin \phi^{j}_{ipp,r,k} \right)$$
여기서, $\lambda_{ipp}$는 IPP의 태양 고정(sun-fixed) 경도, $\phi_{ipp}$는 IPP 지자기(geomagnetic) 위도를 의미한다. $C$와 $S$는 SHE 모델 매개변수를 의미하며, $P$는 정규화된 르장드르 연관 함수(normalized associated Legendre function)를 의미한다.
Eqs. (3, 4)에서 전리층과 위성/수신기 IFB가 결합된 항은 Eqs. (5, 6)에 의해 분리가 가능하지만, 위성과 수신기 IFB는 여전히 선형조합으로 구성되기 때문에 완벽히 분리해서 추정할 수 없다. 본 연구에서는 위성/수신기 IFB가 기준 위성의 IFB에 의해 차분되어 있다고 정의하며, 이에 따라 Eqs. (3, 4)는 Eqs. (7, 8)과 같이 모델링이 가능하다.
$$\tilde{\rho}^{j}_{r,G,1C2W,k} = \alpha_{G,1C2W} F^{j}_{r,k} I^{j}_{V,r,k} + \left( B_{r,G,1C2W} – b^{o}_{G,1C2W} \right) + \left( b^{j}_{G,1C2W} – b^{o}_{G,1C2W} \right) + v^{j}_{r,G,1C2W,k}$$
$$\tilde{\rho}^{j}_{r,E,1X5X,k} = \alpha_{E,1X5X} F^{j}_{r,k} I^{j}_{V,r,k} + \left( B_{r,E,1X5X} – b^{q}_{E,1X5X} \right) + \left( b^{j}_{E,1X5X} – b^{q}_{E,1X5X} \right) + v^{j}_{r,E,1X5X,k}$$
여기서, $o$와 $q$는 각각 GPS와 Galileo의 기준 위성을 의미한다. Eqs. (7, 8)과 같이 위성/수신기 IFB를 모델링 하면, 필터의 계수 부족(rank deficient) 문제가 발생하지 않으며, 상대적인 위성과 수신기 IFB를 분리하는 것이 가능하다.
Eqs. (6-8)로부터 Kalman 필터의 상태변수는 Eq. (9)와 같이 정의할 수 있다.
$$\begin{align}
X_{k} &= \begin{bmatrix} X_{SHE,k} & X_{RIFB,k} & X_{SIFB,k} \end{bmatrix}^{T} \nonumber \\
X_{SHE,k} &= \begin{bmatrix} C_{00,k} & C_{10,k} & C_{11,k} & S_{11,k} & C_{20,k} & C_{21,k} & S_{21,k} & C_{22,k} & S_{22,k} \end{bmatrix} \nonumber \\
X_{RIFB,k} &= \begin{bmatrix} B^{o}_{1,G,1C2W,k} & \cdots & B^{q}_{1,E,1X5X,k} & \cdots & B^{q}_{M,E,1X5X,k} \end{bmatrix} \nonumber \\
X_{SIFB,k} &= \begin{bmatrix} b^{o}_{G,1C2W,k} & \cdots & b^{No}_{G,1C2W,k} & b^{1q}_{E,1X5X,k} & \cdots & b^{Jq}_{E,1X5X,k} \end{bmatrix}
\end{align}$$
여기서, $X_{SHE}$는 SHE 모델 매개변수 벡터, $X_{RIFB}$는 수신기 IFB 벡터, 그리고 $X_{SIFB}$는 위성 IFB 벡터를 의미한다. M은 기준국의 개수, N은 GPS 위성의 개수, J는 Galileo 위성의 개수를 의미하며, 기준 위성 IFB에 의해 차분된 위성/수신기 IFB는 Eq. (10)같이 정의한다.
$$\begin{align}
B^{o}_{r,G,1C2W} &= B_{r,G,1C2W} – b^{o}_{G,1C2W} \nonumber \\
B^{q}_{r,E,1X5X} &= B_{r,E,1X5X} – b^{q}_{E,1X5X} \nonumber \\
b^{jo}_{G,1C2W} &= b^{j}_{G,1C2W} – b^{o}_{G,1C2W} \nonumber \\
b^{jq}_{E,1X5X} &= b^{j}_{E,1X5X} – b^{q}_{E,1X5X}
\end{align}$$
Kalman 필터는 크게 시 전달(time propagation) 부분과 측정 갱신(measurement update) 부분으로 나뉜다. 이전 시점의 후 추정값을 시 전달하기 위해 상태 천이 행렬 및 프로세스 잡음 공분산 행렬을 정의하여야 한다. 본 연구에서 SHE 매개변수는 Random Walk으로 모델링하며, 공정 잡음의 분산은 Chen et al. (2023)에 제시된 방법을 사용하여 설정한다. 위성 및 수신기 IFB는 장기간 안정성을 가진다고 가정하며, 본 연구에서는 상수로 모델링 한다. 상태 천이 행렬과 공정 잡음의 공분산 행렬은 Eqs. (11, 12)와 같이 정의한다.
$$\Phi = \begin{bmatrix}
I_{9} & O & O \\
O & I_{2M} & O \\
O & O & I_{(N+J-2)}
\end{bmatrix}$$
$$Q_k = \begin{bmatrix}
Q_{SHE,k} & O & O \\
O & Q_{RIFB} & O \\
O & O & Q_{SIFB}
\end{bmatrix}$$
여기서, $I_n$은 n×n 단위 행렬을 의미하며, $Q_{SHE}$, $Q_{RIFB}$, 그리고 $Q_{SIFB}$는 각각 SHE 매개변수, 수신기 IFB, 그리고 위성 IFB에 대한 공정 잡음 공분산 행렬을 의미한다.
Kalman 필터의 측정 갱신에 사용하는 관측 행렬(observation matrix) 및 측정 벡터(measurement vector)는 Eqs. (13, 14)와 같다.
$$Y_k = \begin{bmatrix}
y_{1,G,k} \\
y_{1,E,k} \\
\vdots \\
y_{M,G,k} \\
y_{M,E,k}
\end{bmatrix}
= \begin{bmatrix}
\tilde{\rho}^{1o}_{1,G,1C2W,k} & \cdots & \tilde{\rho}^{No}_{1,G,1C2W,k} \\
\tilde{\rho}^{1q}_{1,E,1X5X,k} & \cdots & \tilde{\rho}^{Jq}_{1,E,1X5X,k} \\
\vdots & \ddots & \vdots \\
\tilde{\rho}^{1o}_{M,G,1C2W,k} & \cdots & \tilde{\rho}^{No}_{M,G,1C2W,k} \\
\tilde{\rho}^{1q}_{M,E,1X5X,k} & \cdots & \tilde{\rho}^{Jq}_{M,E,1X5X,k}
\end{bmatrix}^T$$
$$H_k = \begin{bmatrix}
h_{SHE,1,G,k} & h_{RIFB,1} & O & h_{SIFB,G} & O \\
h_{SHE,1,E,k} & O & h_{RIFB,1} & h_{SIFB,E} & \cdots \\
\vdots & \vdots & \vdots & \vdots & \ddots \\
h_{SHE,M,G,k} & h_{RIFB,M} & O & h_{SIFB,G} & O \\
h_{SHE,M,E,k} & O & h_{RIFB,M} & O & h_{SIFB,E}
\end{bmatrix}$$
여기서, G와 E는 GPS와 Galileo 위성군에 대한 지시자를 의미하며, M은 수신기의 개수, 그리고 N과 J는 각각 GPS와 Galileo 위성의 개수를 의미한다. o와 q는 각각 GPS와 Galileo의 기준 위성을 의미한다. $h_{RIFB,r}$은 r-번째 열벡터가 모두 1인 M×M 행렬을 의미하며, $h_{SIFB,G}$와 $h_{SIFB,E}$는 각각 N×N 단위행렬과 J×J 단위 행렬을 의미한다.
위성항법시스템 또는 보강항법시스템과 같이 감시국이나 기준국을 활용하는 시스템의 경우, 지상 장비(ground segment)의 고장이나 유지보수에 의해 감시국/기준국의 중단(outage)이 발생할 수 있다. 또한, 지역적인 분포를 가지는 감시국이나 기준국을 활용하는 시스템은 가시위성의 변화를 고려하여 보강데이터를 생성하여야 한다. 본 연구는 지역적인 기준국 네트워크와 Kalman 필터를 사용하여 순차적으로 전리층 지연과 기준 IFB에 대해 상대적인 위성/수신기 IFB를 추정하며, 기준 IFB는 활용하는 위성군 별로 한 기의 기준국 또는 위성에 대해 설정이 가능하다. 감시국/기준국 수신기의 중단(outage) 또는 위성의 가시성에 따라 기준 IFB가 포함된 측정데이터가 존재하지 않을 경우, 해당시점의 관측 행렬은 가관측하지 않게 된다. 따라서, 측정데이터에 기준 기준국 또는 위성이 포함되는지 여부에 따라 기준 IFB를 변경해주어야 한다.
본 연구에서는 기준 IFB를 각 위성군 별 한기의 위성으로 정의하며, 위성의 가시성 또는 중단(outage) 여부에 따라 기준 IFB를 변경한다. 본 연구에서 정의한 상태변수는 Eq. (9)와 같으며, 기준 위성 IFB 변경을 위해 Eq. (15)와 같이 정의한다.
$$X_{k-1}(o_k, q_k) = \Gamma_{k,k-1} X_{k-1}(o_{k-1}, q_{k-1})$$
여기서 $X_{k-1}(a, b)$는 a-번째 GPS 위성과 b-번째 Galileo 위성 IFB를 기준으로 한 (k-1) 시점의 상태변수를 의미한다. $\Gamma_{k,k-1}$은 기준 위성 IFB 변경에 따라 상태변수를 변경해 주는 행렬을 의미하며, Eq. (16)과 같다.
$$\Gamma_{k,k-1} = \begin{bmatrix}
I_{9} & O & O & O \\
O & I_{M} & O & O \\
O & O & I_{I} – \Lambda_{I \times I}(o_k) & O \\
O & O & O & I_{J} – \Lambda_{J \times J}(q_k)
\end{bmatrix}$$
여기서, $I_n$은 n×n 단위 행렬을 의미하며, $\Lambda_{m \times n}(a)$는 a-번째 열이 모두 1로 구성된 m×n 행렬을 의미한다. 기준 위성 IFB 변경에 따라 오차 공분산 행렬은 Eq. (16)을 사용하여 Eq. (17)과 같이 변경이 가능하다.
$$P_{k-1}(o_k, q_k) = \Gamma_{k,k-1} P_{k-1}(o_{k-1}, q_{k-1}) \Gamma_{k,k-1}^T$$
설계된 Kalman 처리 절차는 Fig. 1과 같다. Fig. 1에서 $\bar{X}$과 $\hat{X}$은 각각 전/후 추정값을 의미하며, 과 는 각각 전/후 추정 오차 공분산 행렬을 의미한다.
Kalman 필터의 초기화 단계(initialization)에서는 사전에 정의된 필터 상태변수와 오차 공분산 정보를 사용한다. 먼저, SHE 매개변수의 초기값은 0으로 설정하거나 IONosphere Map Exchange 데이터로부터 추정된 매개변수를 사용하여 설정이 가능하다. 차분된 위성 IFB의 초기값은 모두 0으로 설정하며, 차분된 수신기 IFB의 초기값은 Fitted Receiver Bias 기법 (Ma & Maruyama 2003)을 사용하여 설정한다. Kalman 필터 상태변수에 대한 오차 분산의 초기값은 경험적인 값을 사용하여 설정할 수 있으며, 본 연구에서는 상태변수가 필터에 의해 수렴이 가능하도록 충분히 큰 값(100.0 m2)으로 초기값을 설정한다.
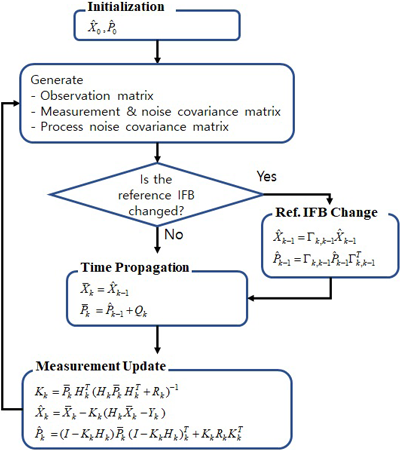
Fig. 1. Implantation of Kalman filter.
필터의 초기화가 완료된 이후, 관측 행렬, 측정 벡터 및 오차 공분산 행렬, 공정 잡음 오차 공분산 행렬을 생성한다. 관측 행렬과 측정 벡터를 생성하는 단계에서 기준 IFB의 변화 여부를 판단하고, 기준 IFB가 변화되었을 경우에 이전 시점의 후 추정값과 오차 공분산 행렬을 새로운 기준 IFB로 변경한다. 기준 IFB 변화가 없거나 후 추정값과 오차 공분산 행렬의 변경이 완료된 이후에 시 전달과 측정 갱신을 수행한다.
이기종 수신기 또는 서로 다른 Firmware를 사용하는 수신기 사이에 각 위성 채널별로 수십 cm 정도의 편이(bias)가 발생할 수 있다는 연구결과가 있으며 (Hauschild & Montenbruck 2016), 이를 Inter-Receiver Satellite Bias (IRSB)라 한다. IGS의 경우, 전 지구에 넓게 분포된 다양한 수신기를 활용하여 위성과 수신기 IFB를 추정하며 (Montenbruck et al. 2014), IRSB의 영향이 완화된 값을 추정한다.
지역적으로 제한되고 독립된 위성항법시스템이나 보강항법시스템은 시스템의 안전성 및 유지보수성 측면에서 동종 수신기/안테나로 구성된 기준국 네트워크를 활용하게 되며, 본 연구에서는 이와 유사하게 동종 수신기/안테나를 사용하여 네트워크를 구성하여 시험을 수행한다.
본 연구에서 설계 및 구현한 Kalman 필터의 기능 및 성능을 분석하기 위해 국내 상시 기준국을 활용한다. 국내는 200여개 이상의 상시 기준국이 운용 중에 있으며, GNSS 데이터 통합센터를 통해 후처리용 RINEX 데이터를 다운로드할 수 있다 (GNSS Data Center 2024). 기준국을 선정하기 위해 GPS L1 C/A 코드(C1C)와 L2 P(Y) 코드(C2W) 그리고 Galileo E1 C 코드(C1C)와 E5a I+Q 코드(C5X)가 활용가능한 기준국을 우선적으로 선정한다. 다음으로 국내 상시 기준국 중 기준국의 분포를 최대한 넓게 하면서, 동일 수신기와 안테나/돔을 가지는 6개의 기준국을 최종적으로 선정한다. 선정한 기준국의 분포는 Fig. 2와 같으며, 수신기와 안테나/돔의 형태는 Table 1과 같다.
데이터 수집기간은 전리층 활동이 활발하지 않은 임의의 날로 선정하며, 2023년 7월 10일(DOY:191)부터 14일(DOY:195)까지 총 5일간의 데이터를 수집한다. 수집한 데이터는 50초 간격으로 처리한다.
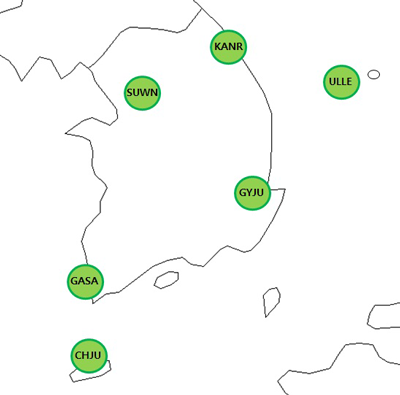
Fig. 2. Distribution of reference stations.
Table 1. Information of the selected reference stations.
| Station name | Receiver | Antenna (dome) | |
|---|---|---|---|
| 1 | CHJU | Trimble NetR9 | TRM 59800.00 (SCIS) |
| 2 | GASA | Trimble NetR9 | TRM 59800.00 (SCIS) |
| 3 | GYJU | Trimble NetR9 | TRM 59800.00 (SCIS) |
| 4 | KANR | Trimble NetR9 | TRM 59800.00 (SCIS) |
| 5 | SUWN | Trimble NetR9 | TRM 59800.00 (SCIS) |
| 6 | ULLE | Trimble NetR9 | TRM 59800.00 (SCIS) |
IGS에서 사용하는 위성/수신기 IFB 추정 기법은 전 지구에 넓게 분포한 수신기를 사용하고, 하루 동안 누적된 측정데이터를 기반으로 한다. 본 연구는 지역적으로 한정된 수신기 네트워크를 사용하고, 순차적인 데이터 처리를 수행함에 따라 일정 시간내에 획득가능한 측정데이터가 IGS에 비해 상대적으로 적다. 뿐만 아니라, 본 연구에서 사용하는 전리층 모델은 측정데이터가 존재하는 영역에서만 정확한 특성을 가지기 때문에, Kalman 필터의 시 전달 단계에서 사용하는 공정 잡음 오차 공분산을 상대적으로 크게 설정하여야 한다. 이에 따라, 본 연구에서 설계 및 구현한 Kalman 필터의 수렴 시간은 위성 채널별 가용시간과 SHE 매개변수의 수렴 시간을 고려하여 2일로 설정하고, 총 5일 중 수렴 시간인 2일을 제외한 나머지 3일간의 추정값을 사용하여 성능 분석을 수행한다.
설계 및 구현한 Kalman 필터의 성능은 상대적인 수신기 IFB의 안정성(stability)과 위성 IFB의 정확성 측면으로 분석한다. 데이터 처리를 통하여 추정된 수신기 IFB는 기준 위성 IFB에 대해 상대적인 값을 가지며, Fig. 3과 같은 결과가 생성된다. 수신기 IFB 추정의 안정성을 분석하기 위해서는 임의의 수신기 IFB 기준으로 값을 수준화(leveling) 하여야 하며, ULLE 수신기 IFB 기준으로 수준화 된 수신기 IFB 추정값은 Fig. 4와 같다. Table 2는 수준화 된 수신기 IFB의 평균값과 표준편차를 보여준다. Fig. 4와 Table 2로부터 Kalman 필터의 수렴기간 이후 수준화 된 수신기 IFB가 표준편차 0.03 ns 이내의 값을 가지고 안정적으로 산출되는 것을 확인할 수 있다.
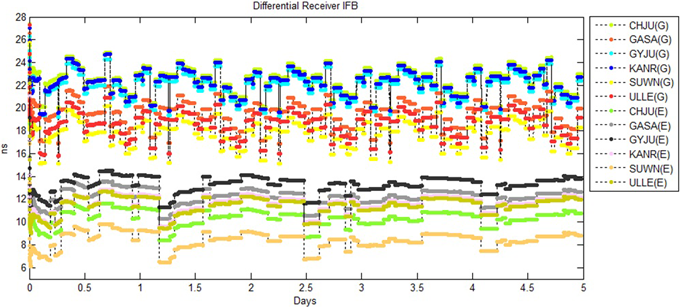
Fig. 3. Differential receiver IFB estimates.
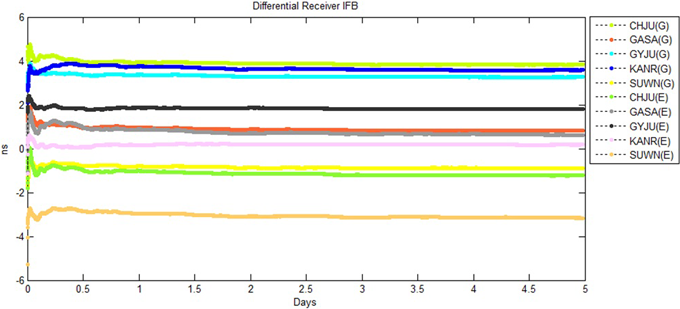
Fig. 4. Leveled differential receiver IFBs by ULLE receiver.
Table 2. Stability of differential receiver IFB (unit: ns).
| Receiver | GPS | Galileo | |||
|---|---|---|---|---|---|
| Mean | STD | Mean | STD | ||
| 1 | CHJU-ULLE | 3.84 | 2.30E-02 | -1.20 | 3.00E-02 |
| 2 | GASA-ULLE | 0.84 | 1.92E-02 | 0.67 | 2.96E-02 |
| 3 | GYJU-ULLE | 3.27 | 1.22E-02 | 1.81 | 1.99E-02 |
| 4 | KANR-ULLE | 3.60 | 2.64E-02 | 0.19 | 1.03E-02 |
| 5 | SUWN-ULLE | -0.88 | 9.00E-03 | -3.12 | 2.51E-02 |
위성 IFB 추정 성능 분석을 위해 Kalman 필터로부터 추정된 GPS와 Galileo의 상대적인 위성 IFB를 수준화 한다. 수준화는 각 위성군에 속하는 위성 IFB 합이 0이라는 조건을 활용한다. Fig. 5는 수준화가 완료된 이후 위성 IFB 추정값의 평균과 Deutsches Zentrum Für Luft-und Raumfahrt (DLR), Chinese Academy of Sciences (CAS), Center for Orbit Determination in Europe (CODE)에서 제공하는 Differential Code Bias (DCB) 값을 도시한다. DLR, CAS, 그리고 CODE에서 제공하는 DCB 값은 각 위성의 Antenna Phase Center Offset이 보정된 값이기 때문에, IGS에서 제공하는 안테나 모델인 IGS20을 사용하여 재보정을 수행한다 (IGS 2023). Fig. 6은 위성 IFB 추정 값의 표준편차를 보여준다. Fig. 5로부터 본 연구에서 설계 및 구현된 Kalman 필터가 IGS에서 제공하는 각 위성별 DCB와 유사한 위성 IFB 값을 추정하는 것을 확인할 수 있으며, Fig. 6으로부터 추정된 위성 IFB가 0.25 ns 이내로 산출되는 것을 확인할 수 있다.
Fig. 7은 Fig. 5로부터 산출된 오차의 RMS 값을 도시하며, Table 3은 각 위성군 별 RMS 오차의 평균과 최대 RMS 오차를 제시한다. Fig. 7로부터 G06과 G29를 제외한 모든 위성 IFB 추정 오차의 RMS가 1 ns 이내로 산출됨을 확인할 수 있으며, CODE에서 제공하는 위성 DCB와의 오차가 가장 작게 산출된 것을 확인할 수 있다. Table 3으로부터 Galileo 위성에 대한 RMS 오차의 평균과 최대 RMS 값은 세 개의 DCB에 대해 모두 0.3 ns가 산출되었으며, E34 위성에서 가장 큰 RMS 오차가 발생함을 확인할 수 있다. GPS의 경우, DLR과 CAS에서 제공하는 DCB 대비 평균 0.5 ns의 RMS 오차가 발생하였으며, CODE에서 제공하는 DCB 대비 0.3 ns의 평균 RMS 오차가 발생함을 확인하였다. Fig. 7과 Table 3의 결과로부터 GPS 위성 IFB 추정값에 대한 RMS 오차가 Galileo 위성보다 크게 나타나는 것을 확인할 수 있다. 본 연구에서는 동종 수신기/안테나로 구성된 기준국 네트워크를 활용함에 따라, IRSB가 포함된 위성 IFB를 추정하게 된다. IRSB는 수신기의 종류와 firmware 뿐 아니라 각 위성군에서 사용하는 신호 생성 방식에 따라 다르며, Galileo 위성 신호가 GPS 위성 신호에 비해 더 작은 IRSB를 발생시킨다는 연구결과가 있다 (Hauschild & Montenbruck 2016). 따라서, GPS 위성 IFB 추정 오차가 Galileo 위성보다 크게 도출되는 원인은 IRSB의 영향에 의한 것으로 판단할 수 있다.
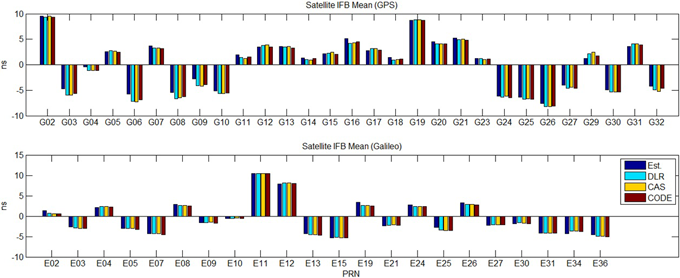
Fig. 5. Leveled differential satellite IFBs vs. IGS DCB product.
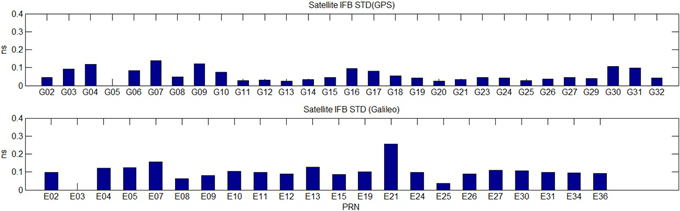
Fig. 6. Standard deviations for leveled differential satellite IFBs.
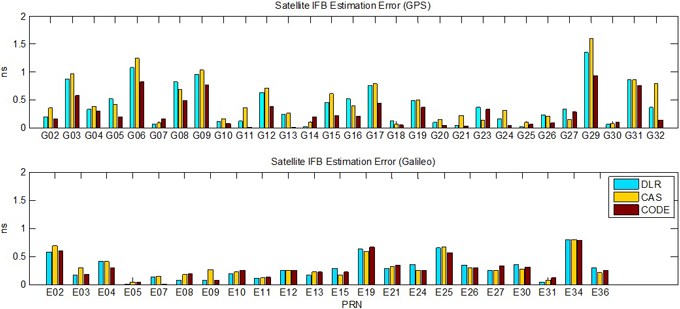
Fig. 7. Satellite IFB estimation errors.
Table 3. RMS errors w.r.t. three different IGS product (unit: ns).
| Satellite DCB product source | GPS | Galileo | |||
|---|---|---|---|---|---|
| Average | Max. | Average | Max. | ||
| 1 | DLR | 0.43 | 1.30 | 0.29 | 0.85 |
| 2 | CAS | 0.48 | 1.55 | 0.30 | 0.85 |
| 3 | CODE | 0.29 | 0.89 | 0.29 | 0.83 |
위성/수신기 IFB는 위성항법시스템 또는 보강항법시스템에서 정밀한 항법데이터나 보강데이터를 생성하기 위해 필수적으로 추정하거나 제거하여야 한다. 본 연구에서는 지역적인 수신기 네트워크를 활용하여 준 실시간으로 위성/수신기 IFB를 순차적으로 추정하기 위한 Kalman 필터를 설계 및 구현하였다. 지역적으로 제한된 수신기 네트워크를 활용하여 위성/수신기 IFB를 추정하기 위해 기존 연구를 기반으로 전리층 모델과 이에 대한 공정잡음을 모델링하였다. 이와 함께, 별도의 제약사항을 적용하지 않고 기준 IFB에 대해 상대적인 위성/수신기 IFB를 추정하기 위한 측정 모델을 제안하였다. 이와 함께, 실 운영 환경에서 제안된 방법의 연속성을 확보하기 위해 기준 IFB의 변화를 고려한 Kalman 필터를 설계 및 구현하였다.
설계 및 구현된 Kalman 필터의 성능을 분석하기 위해 6곳의 국내 상시기준국을 선정하였으며, 총 5일간의 연속된 데이터를 활용하여 데이터 처리를 수행하였다. 본 연구를 통해 구현된 필터의 경우, 지역적으로 한정된 영역을 기반으로 하기 때문에 안정된 추정값이 산출되기까지 약 2일 정도가 소요되는 것을 확인하였으며, 5일 중 안정화 기간(2일)을 제외한 3일간의 추정 결과를 사용하여 성능 분석을 수행하였다. 수신기 IFB 추정 성능은 안정성 측면에서 분석하였으며, 0.03 ns 이내의 편차를 가지면서 안정적으로 추정됨을 확인하였다. 위성 IFB 추정 성능은 추정의 안정성과 정확성 측면에서 분석하였다. 위성 IFB는 필터의 수렴이후, 약 0.25 ns 이내의 편차를 가지고 추정되는 것을 확인하였다. 위성 IFB 추정의 정확성을 분석하기 위해 세개의 다른 기관에서 제공하는 위성 DCB 데이터를 사용하였다. 위성 IFB 추정 오차의 평균 RMS는 0.29~0.48 ns로 산출되었으며, 위성 채널별 최대 RMS 오차는 GPS와 Galileo 각각 1.55 ns와 0.85 ns로 산출되었다.
본 연구 결과, 수신기 IFB는 높은 안정성을 가지며 추정되는 것을 확인하였으나, 일부 위성 IFB의 경우에는 추정의 안정성과 정확성이 낮아지는 것을 확인하였다. 추정의 안정성이 낮아지는 것은 지역적으로 한정된 환경에서 사용가능한 위성의 측정데이터가 하루 중 3~6시간 정도밖에 되지 않기 때문으로 분석이 가능하며, 안정성이 높지만 정확성이 낮아지는 것은 IRSB와 같이 모델링 되지 않은 추가적인 편이가 추정 정확도에 영향을 주었을 것으로 예상이 가능하다.
본 연구는 국토교통부 항공안전기술개발사업 연구비지원 (RS-2021-KA164208)에 의해 수행되었습니다.
Conceptualization, M.Son and H.Kim; methodology, M.Son and H.Kim; software, H.Kim; validation, H.Kim; formal analysis, M.Son and H.Kim; investigation, H.Kim; resources, M.Son; data curation, M.Son; writing—original draft preparation, H.Kim; writing—review and editing, H.Kim and M.Son; visualization, H.Kim; supervision, H.Kim and M.Son; project administration, M.Son; funding acquisition, M.Son.
The authors declare no conflict of interest.
Authié, T., Dall’Orso, M., Trilles, S., Choi, H. H., Kim, H. S., et al. 2017, Performances Monitoring and Analysis for KASS, International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, Oregon, USA, 25-29 Sep 2017, pp.958-978. https://doi.org/10.33012/2017.15405
Chen, P., Zhang, Y., Wang, R., An, Z., & Yao, Y. 2023, A Novel Approach for Establishing the Global Ionospheric Model with High Spatiotemporal Resolution, in IEEE Transactions on Geoscience and Remote Sensing, 61, 1-12. https://doi.org/10.1109/TGRS.2023.3238044
Choi, B. K., Lee, W. K., Cho, S. K., Park, J. U., & Park, P. H. 2010, Global GPS Ionospheric Modelling Using Spherical Harmonic Expansion Approach, Journal of Astronomy and Space Sciences, 27, 359-366. https://doi.org/10.5140/jass.2010.27.4.359
Erdogan, E., Schmidt, M., Seitz, F., & Durmaz, M. 2017, Near real-time estimation of ionosphere vertical total electron content from GNSS satellites using B-splines in a Kalman filter, Annales Geophysicae, 35, 263-277. https://doi.org/10.5194/angeo-35-263-2017
GNSS Data Center, Data Service, cited 2024 June 25, available from: https://www.gnssdata.or.kr/
Han, D. H. 2018, A Study on Improving the Accuracy of SBAS Ionosphere Correction by Applying Double-difference Carrier Phase Measurements, Ph.D. Thesis, Seoul National University.
Hauschild, A. & Montenbruck, O. 2016, The Effect of Correlator and Front-End Design on GNSS Pseudorange Biases for Geodetic Receivers, Journal of the Institute of Navigation, 63, 443-453. https://doi.org/10.1002/navi.165
International GNSS Service (IGS) 2018, RINEX-The Receiver Independent Exchange Format (Version 3.04), RINEX WG & RTCM-SC104. https://files.igs.org/pub/data/format/rinex304.pdf
International GNSS Service (IGS) 2023, IGS switch to IGS20/igs20.atx and repro3 standards, cited 2023 Jan 21, available from: https://igs.org/news/igs20/
International GNSS Service (IGS) 2024, MGEX Data & Product: Differential Code Biases, cited 2024 Feb 28, available from: http://igs.org/mgex/data-products/#dcb
Kim, J., Noh, J. H., & Lee, H. K. 2012, Error Analysis of Inter-Frequency Bias Estimation in Global Navigation Satellite System Signals, Journal of the Korean Society for Aviation and Aeronautics, 20, 16-21. https://doi.org/10.12985/ksaa.2012.20.3.016
Ma, G. & Maruyama, T. 2003, Derivation of TEC and estimation of instrumental biases from GEONET in Japan, Annales Geophysicae, 21, 2083-2093. https://doi.org/10.5194/angeo-21-2083-2003
Maheshwari, M., Nirmala, S., Kavitha, S., & Ratanakara, S. C. 2019, Kalman filter based estimation of differential hardware biases with triangular interpolation technique for IRNSS, Advances in Space Research, 63, 1051-1064. https://doi.org/10.1016/j.asr.2018.09.031
Montenbruck, O., Hauschild, A., & Steigenberger, P. 2014, Differential Code Bias Estimation using Multi-GNSS Observations and Global Ionosphere Maps, Journal of Institute of Navigation, 61, 191-201. https://doi.org/10.1002/navi.64
Schaer, S. 1999, Mapping and predicting the Earth’s ionosphere using the Global Positioning System, Ph.D. Thesis, Astronomical Institute, University of Berne, Switzerland.
Steigenberger, P., Montenbruck, O., & Hessels, U. 2015, Performance evaluation of the early CNAV navigation message, Journal of the Institute of Navigation, 62, 219-228. https://doi.org/10.1002/navi.111
Sunehra, D. 2016, TEC and Instrumental Bias Estimation of GAGAN Station Using Kalman Filter and SCORE Algorithm, Positioning, 7, 41-50. https://doi.org/10.4236/pos.2016.71004
Tetewsky, A., Ross, J., Soltz, A., Vaughn, N., Anszperger, J., et al. 2009, Making sense of inter-signal corrections: accounting for GPS satellite calibration parameters in legacy and modernized ionosphere correction algorithms, Inside GNSS, Jul/Aug 2009, available from: https://insidegnss.com/
Walter, T., Blanch, J., Phelts, R. E., & Enge, P. 2012, Evolving WAAS to serve L1/L5 users, Navigation, 59, 317-327. https://doi.org/10.1002/navi.21
Wang, A., Chen, J., Zhang, Y., Wang, J., & Wang, B. 2019a, Performance Evaluation of the CNAV Broadcast Ephemeris, Journal of Navigation, 72, 1331-1344. https://doi.org/10.1017/S037346331900016X
Wang, N., Li, Z., Montenbruck, O., & Tang, C. 2019b, Quality assessment of GPS, Galileo and BeiDou-2/3 satellite broadcast group delays, Advances in Space Research, 64, 1764-1779. https://doi.org/10.1016/j.asr.2019.07.029
Wang, Y., Zhao, L., & Gao, Y. 2021, Estimation and Analysis of GNSS Differential Code Biases (DCBs) Using a Multi-Spacing Software Receiver, Sensors, 21, 443. https://doi.org/10.3390/s21020443
Yun, H., Han, D. H., & Kee, C. D. 2013, Performance Verification of Korean Wide Area Differential GNSS Ground Segment, Journal of Navigation and Port Research, 37, 49-54. https://doi.org/10.5394/KINPR.2013.37.1.49
Zhang, Q. & Zhao, Q. 2019, Analysis of the data processing strategies of spherical harmonic expansion model on global ionosphere mapping for moderate solar activity, Advances in Space Research, 63, 1214-1226. https://doi.org/10.1016/j.asr.2018.10.031