Department of Aerospace Engineering, Korea Advanced Institute of Science and Technology, Daejeon 34141, Korea
Citation: Kim, N. M., Min, D., & Lee, J. 2025, Improved Z-Matrix Search Algorithm for Enhanced Integer Ambiguity Estimation and Fix Reliability in RTK, Journal of Positioning, Navigation, and Timing, 14, 203-210.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 203-210. https://doi.org/10.11003/JPNT.2025.14.3.203
Received on Aug 10, 2025, Revised on Aug 18, 2025, Accepted on Aug 19, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Reliable integer ambiguity resolution is essential for high-precision, high-integrity Real Time Kinematic (RTK) positioning. The probability of correct fix (P(CF)) provides a key metric for assessing ambiguity resolution reliability and is directly influenced by the integer decorrelation matrix (Z-matrix) performance. This paper proposes an enhanced Z-matrix search method to improve the reliability of integer ambiguity estimation. The method extends the conventional LAMBDA algorithm by generating multiple Z-matrix candidates through systematic linear transformations and expands the search space to select the most reliable candidate based on P(CF). Simulation results from 24-hour single-epoch RTK show the proposed method improves P(CF) in over 97.5% of epochs, reduces the average 1−P(CF) value by approximately 64.1%, and increases fixed solution availability from 85.7% to 95.3%. Although the validation was performed using single-epoch RTK, the proposed method applies to general RTK architectures, including Kalman filter-based systems, and should contribute to faster convergence and more robust ambiguity resolution.
global navigation satellite system, RTK, Z-matrix, probability of correct fix
민간 항공에서 항법 무결성은 항법 시스템의 가용성에 영향을 미치는 중요한 성능 지표이다. 글로벌 위성항법시스템(Global Navigation Satellite System, GNSS)에서 무결성 위험은 위치 오차가 미리 정의된 경보 한계(Alert Limit, AL)를 초과할 확률로 정의된다. 예를 들어, 지상 기반 보강 항법 시스템(Ground-Based Augmentation System, GBAS)을 사용한 민간 항공기 착륙의 경우 카테고리 III 정밀 접근을 위해 수직 경보 한계(Vertical Alert Limit, VAL) 10 m에서 접근당 10⁻⁹의 극도로 낮은 무결성 위험 수준이 요구된다 (Enge 1999). GBAS 응용 분야에 대한 이러한 무결성 요구사항은 정확도 요구사항(예: 수직 95% 정확도 2.5 m (Enge 1999))보다 훨씬 더 엄격한 수준이다. 그러나 미래 도심에서 운용될 자율주행 자동차나 무인 항공기와 같은 자율 운항체는 높은 수준의 무결성과 정확도가 모두 필수적으로 요구될 것이라 전망된다. Reid et al. (2019)은 자율주행 자동차의 운용을 위한 항법 요구사항을 제안했는데, 고속도로 운행을 위해 수직 정확도 0.44 m와 수직 경보 한계 1.3 m에서 시간당 10⁻⁸의 무결성 위험 요구사항을 포함한다. 이러한 항법 정확도를 안정적으로 만족하기 위해서는 기존 코드 측정치 기반 항법 시스템만으로는 한계가 있다. 그에 따라 반송파 측정치를 활용하여 cm 레벨 항법 정확도를 나타내는 실시간 이동 측위(Real Time Kinematic, RTK) 항법 시스템에 대한 수요가 높아지고 있다.
RTK는 기준국과 유저 간 이중 차분 측정치를 활용하여 상대 위치를 고정밀로 추정하는 기법이다. 이 과정에서 반송파 측정치 내 미지정수를 정확히 참값과 일치하는 정수해로 고정해야 높은 정확도의 RTK 고정 위치해를 산출할 수 있다. 여기서 고정 위치해란 미지정수를 정수값으로 고정한 후 산출되는 위치해를 의미하며, 미지정수를 실수값으로 추정하는 실수 위치해와 구별된다. 미지정수가 잘못 고정될 경우, 크기를 알 수 없는 위치 바이어스를 유발하고, 이는 자율주행 및 항공 분야에서 치명적인 무결성 위협이 될 수 있다. 따라서 RTK 항법 시스템의 무결성 보장을 위해서는 고정된 정수해가 참값과 일치할 확률(Probability of Correct Fix, P(CF))을 사전에 평가하고, 무결성 위협 확률 산출 과정에 반영해야 한다.
P(CF)는 미지정수를 정수로 고정하는 과정에서 산출되며, 대표적인 미지정수 고정 알고리즘으로 정수 반올림법(Integer Rounding, IR), 정수 부트스트래핑법(Integer Bootstrapping, IB), 그리고 정수 최소자승법(Integer Least Squares, ILS)이 있다. 이론적으로 ILS는 최적의 미지정수 고정 성능을 보이며 (Teunissen 1999), 오픈소스로 공개되어 있는 미지정수 고정 알고리즘인 Least-squares Ambiguity Decorrelation Adjustment (LAMBDA) 기법에서도 이를 채택하고 있다. 그러나 ILS 기법은 복잡한 정수 탐색 영역을 가지고 있어, P(CF) 값을 정확히 산출하는 것이 불가능하다는 한계점이 있다. 반면, IB 기법은 ILS 기법에 비해 미지정수 추정 성능은 다소 저하되지만, P(CF) 값을 직관적으로 계산할 수 있다는 장점이 있다 (Teunissen 1998). RTK 항법 해의 무결성 위협 확률 산출을 위해서는 P(CF) 값이 필수적이므로, 일반적으로 다음과 같은 두 가지 접근 방법이 가능하다: (1) IB 기법을 사용하여 미지정수 고정과 P(CF) 산출을 수행하거나, (2) ILS 기법으로 미지정수를 고정한 후 IB 기반 P(CF) 값을 보수적인 하한값으로 적용하는 방법이다.
결과적으로 RTK 항법 시스템의 무결성 보장을 위해서는 IB 기법 기반 P(CF) 값을 산출해야 한다. IB 기법의 미지정수 고정 및 P(CF) 산출 과정은 크게 세 단계로 구성된다 (Teunissen 1998). 먼저, Least-Squares 또는 Kalman Filter 기반으로 미지정수 실수해(float ambiguity)와 그 공분산 행렬을 산출한다. 다음으로, 정수 고정 과정에서 성분 간 상관관계를 줄이기 위해 Z-변환(Z-transformation)을 적용하여 공분산 행렬을 역상관화(decorrelation)한다. 마지막으로, 변환된 공분산 행렬과 미지정수 실수해에 IB 기법을 적용하여 미지정수 정수해 및 P(CF) 값을 산출한다. 이 과정에서 P(CF)는 미지정수 실수해의 공분산 행렬과 역상관화를 위해 적용된 Z-행렬의 성능에 의존한다. 위 과정에 대한 자세한 설명은 본 논문의 2.1절에 기술되어 있다.
Z-변환은 미지정수 간 상관관계를 줄이는 선형 변환이며, 이때 변환에 사용되는 Z-행렬은 모든 성분이 정수이고 행렬식의 절댓값이 1인 가역 행렬이어야 한다 (Teunissen 1995). LAMBDA 기법은 특정 공분산 행렬에 대하여 이러한 조건을 만족하는 Z-행렬을 탐색하기 위한 알고리즘을 포함하고 있으며, 이는 현재 공개된 LAMBDA 오픈소스 라이브러리에도 구현되어 있다. 본 연구에서는 해당 오픈소스 Z-행렬 탐색 알고리즘을 적용했을 때, 미지정수의 수가 많아질수록 Z-행렬 탐색이 조기 종료되어 P(CF) 성능이 저하되는 현상을 발견하였다. 이는 Z-행렬 탐색 알고리즘이 탐색 과정에서 지역 최적해(local optimum)에 수렴하기 때문이다. 그 결과 P(CF)가 감소하고 RTK 고정 위치해의 무결성을 보장하지 못해 가용성이 저하되는 현상이 발생하였다.
이러한 한계를 극복하기 위해, 본 연구에서는 기존의 Z-행렬 탐색 알고리즘의 종료 시점을 개선하여 Z-행렬의 성능을 개선할 수 있는 Z-행렬 후보군 생성 알고리즘을 제안한다. 구체적으로는 기존 알고리즘에서 산출한 Z-행렬에 대해 선형 변환을 적용하고 미지정수 순서를 재조정하여 후보군을 생성하며, 각 후보에 대해 최종 P(CF)를 산출한 후 가장 높은 값을 갖는 Z-행렬을 선택하는 방식이다. 이와 같은 Z-행렬 후보군 생성 기법은 기존 방식 대비 Z-행렬의 최적성 및 P(CF) 성능을 향상시키고, 최종적으로 RTK 고정 위치해의 가용성을 높일 수 있다. 본 논문에서는 제안한 기법의 실용성을 검증하기 위해 GNSS 측정치 모델링 및 RTK 항법 시뮬레이션을 수행하고, 제안한 Z-행렬 후보군 생성 기법 적용에 따른 RTK 고정 위치해의 가용성 개선폭을 분석하였다.
본 논문의 구성은 다음과 같다. 2장에서는 IB 기법 기반 P(CF) 산출 방법론과 RTK 고정 위치해의 보호 수준 산출 방법론에 대해 기술한다. 3장에서는 LAMBDA 기법 내 기존 Z-행렬 탐색 기법과 제안된 후보군 생성 기법에 대해 상세히 설명하고, 4장에서는 시뮬레이션 기반의 성능 분석 결과를 제시한다. 마지막으로 5장에서는 본 연구의 결론 및 향후 연구 방향에 대해 논의한다.
이번 장에서는 IB 기법 기반 P(CF) 산출 방법론과 정상 상황에서 RTK 고정 위치해의 보호 수준 산출 방법론에 대해 설명한다. 2.1절에서는 RTK 항법 알고리즘과 IB 기법 기반 P(CF) 산출 방법론을 설명하고, 2.2절에서는 산출된 P(CF) 값을 활용한 RTK 고정 위치해의 무결성 위협 확률 및 보호 수준 산출 방법론에 대해 기술하였다.
P(CF) 값은 미지정수 실수해를 정수해로 고정하는 과정에서 산출된다. 미지정수 고정 과정은 일반적으로 다음 세 단계로 구성된다 (Teunissen 1998). 첫 단계에서는 이중 차분된 GNSS 코드 및 반송파 측정치를 활용하여 미지정수의 정수 조건을 무시하고, 칼만 필터(Kalman filter) 또는 최소자승법(Least squares) 등을 적용하여 Eq. (1)과 같이 실수 위치해($\hat{b}$) 및 미지정수 실수해($\hat{N}$)를 산출한다.
$$\begin{bmatrix}
\hat{b} \\
\hat{N}
\end{bmatrix},
\quad
\begin{bmatrix}
Q_{\hat{b}} & Q_{\hat{b}\widehat{N}} \\
Q_{\widehat{N}\hat{b}} & Q_{\widehat{N}}
\end{bmatrix}$$
여기서 $Q_{\hat{b}}$와 $Q_{\widehat{N}}$은 각각 실수 위치해와 미지정수 실수해의 공분산 행렬을 나타내고, $Q_{\hat{b}\widehat{N}}$과 $Q_{\widehat{N}\hat{b}}$는 두 해의 상관 행렬을 나타낸다. 측정치에 고장이 발생하지 않은 정상 상황에서 측정치의 오차가 영평균 정규분포를 따른다는 가정 하에, 최소자승법 또는 칼만 필터를 통해 산출되는 실수해의 오차는 마찬가지로 영평균 정규분포를 따른다.
두 번째 단계에서는 산출한 미지정수 실수해($\hat{N}$)를 정수해($\check{N}$)로 변환한다. 이전 단계에서 이중 차분된 GNSS 측정치를 기반으로 미지정수 실수해를 산출하였고, 각 이중 차분 측정치는 공통된 기준 위성 측정치를 포함하고 있기 때문에 미지정수 간 강한 상관관계를 나타낸다. 이러한 강한 상관관계는 미지정수 실수해를 정수로 고정하는 과정을 방해하는 주요 요소 중 하나이다. 따라서 LAMBDA 기법에서는 미지정수 실수해의 각 성분 간 상관관계를 최소화하는 Z-변환을 선행한다 (Teunissen 1995). Z-변환을 통해 미지정수 실수해 및 공분산 행렬은 Eq. (2)와 같이 Z-도메인으로 변환된다.
$$\hat{z} = Z^{T} \widehat{N}, \qquad Q_{\hat{z}} = Z^{T} Q_{\widehat{N}} Z.$$
여기서 Z는 Z-변환 행렬을 나타내고, $\hat{z}$및 $Q_{\hat{z}}$는 Z-변환된 미지정수 실수해와 공분산 행렬을 의미한다. Z-변환 전후에 미지정수의 정수 성질이 유지되어야 하므로, Z-행렬은 모든 성분이 정수이고 역행렬이 존재해야 한다. 미지정수 성분 간 상관관계를 완전히 제거하면서 위 제한 조건을 만족하는 Z-행렬은 존재하지 않는다. 따라서 제한 조건을 만족하면서 상관관계를 최대한 완화시킬 수 있는 Z-행렬을 탐색해야 한다. 일반적으로 미지정수 고정에 활용되는 LAMBDA 기법은 독자적인 Z-행렬 탐색 알고리즘을 포함하고 있으며, 해당 알고리즘에 대한 자세한 설명은 3.1절에 기술하였다.
Z-변환된 미지정수 실수해는 Z-도메인의 탐색 영역 내에서 정수해로 고정된다. 대표적인 미지정수 고정 기법으로 IR, IB, ILS와 같은 고정 기법이 지난 수십 년간 개발되었다 (Teunissen 1999). 본 연구에서는 P(CF) 산출에 용이한 IB 기법을 활용하여 미지정수를 고정하였다. IB 기법은 순차적 조건부 최소자승법을 기반으로 하며, 고정하려는 미지정수의 수를 n이라 정의할 때 다음과 같이 세 단계로 구성된다 (Teunissen 1998). 1) 미지정수 실수해의 k번째 성분을 반올림하여 고정한다. 2) 고정된 k번째 성분을 기반으로 k+1번째부터 n번째까지의 실수해 성분을 보정한다. 3) k=1부터 n까지 위의 과정을 반복해서 수행한다. IB 기법을 통해 보정 및 역상관화된 미지정수 실수해 각 성분의 분산 값은 $Q_{\hat{z}}$의 LDL 분해를 통해 산출되는 대각 행렬 D의 성분과 일치한다 (Teunissen 1998). 그에 따라 P(CF) 값은 D 행렬의 성분 값을 활용하여 Eq. (4)와 같이 산출된다.
$$
Q_{\hat{z}} = L \, D \, L^{T}
$$
$$
P_{CF}(Q_{\widehat{N}}, Z)
= \prod_{i=1}^{n} \left( 2 \Phi\!\left( \frac{1}{2 \sqrt{D_{ii}}} \right) – 1 \right)
$$
여기서 $\Phi$는 표준정규분포의 누적분포함수를 나타내고, $PCF(Q_{\widehat{N}}, Z)$는 미지정수 실수해의 공분산 행렬과 Z-행렬을 입력값으로 산출된 P(CF)를 나타낸다. 이때 미지정수 실수해의 공분산 행렬은 GNSS 가시 위성 수 및 위성 기하, 측위 기법에 따라 결정되는 값이고, Z-행렬 탐색 알고리즘에서 산출된 Z-행렬의 성능에 따라 최종 P(CF) 값이 변화하게 된다.
이번 절에서는 측정치에 고장이 발생하지 않은 정상 상황($H_{0}$)에서 RTK 항법해의 보호수준 산출 방법론에 대해 기술한다. 일반적으로 GNSS 항법 시스템에서는 위성 배치의 기하학적 특성상 수직 방향의 정밀도 저하계수(VDOP)가 수평 방향(HDOP)보다 크므로, 본 절에서는 수직 방향 보호수준(Vertical Protection Level, VPL)을 기준으로 설명한다. 보호수준은 주어진 무결성 위협 확률 요구조건에 대응하는 통계적 위치 오차 한계를 의미하며, 사전 정의된 경보 한계와 비교하여 시스템의 가용성을 판단하는 기준이 된다. 정상 상황에서 RTK 고정 위치해의 무결성 위협 확률 산출 식은 Eq. (5)와 같이 정의된다 (Pervan & Chan 2001).
$$I_{H_{0}} = \mathrm{P}\left\{ \left| \check{b}_{v} – b_{v} \right| > VPL_{H_{0}} \right\}$$
여기서 $\check{b}_{v}$는 RTK 고정 위치해의 수직 방향 성분을 의미하고, $b_{v}$는 실제 위치의 수직 방향 성분을 의미한다. 그리고 $I_{H_{0}}$및 $VPL_{H_{0}}$는 각각 정상 상황에서의 무결성 요구조건 및 수직 방향 보호수준을 의미한다. RTK 고정 위치해는 미지정수가 잘못 고정될 경우 위치 항법해에 바이어스가 발생할 수 있다. 따라서 RTK 고정 위치해의 무결성 위협 확률은 Eq. (6)과 같이 미지정수가 올바르게 결정되었을 경우(Correct Fix, CF)와 잘못 고정되었을 경우(Incorrect Fix, IF)로 나누어 계산되어야 한다.
$$
I_{H_{0}} =
\mathrm{P}\!\left\{ \left| \check{b}_{v} – b_{v} \right| > VPL_{H_{0}} \,\middle|\, CF \right\}
P_{CF}(Q_{\widehat{N}}, Z)
+
\mathrm{P}\!\left( \left| \check{b}_{v} – b_{v} \right| > VPL_{H_{0}} \,\middle|\, IF \right)
\left( 1 – P_{CF}(Q_{\widehat{N}}, Z) \right)
$$
미지정수가 잘못 고정된 상황에서 RTK 고정 위치해의 분포를 정확히 추정하는 것은 불가능하다. 따라서 Pervan & Chan (2001)에서는 보수적으로 미지정수가 잘못 고정되면 위치 오차가 보호수준을 초과한다는 가정을 적용하였고 $\left(
P\!\left\{
\,\bigl|\,\check{b}_{v}-b_{v}\,\bigr|
> VP L_{H_0} \,\middle|\, IF
\right\}
\approx 1
\right)$, 그에 따라 무결성 위협 확률 산출 식은 Eq. (7)과 같이 전개된다.
$$I_{H_{0}} =
\mathrm{P}\!\left\{ \left| \check{b}_{v} – b_{v} \right| > VPL_{H_{0}} \,\middle|\, CF \right\}
P_{CF}(Q_{\widehat{N}}, Z)
+
\left( 1 – P_{CF}(Q_{\widehat{N}}, Z) \right)
$$
최종적으로 주어진 무결성 위협 요구조건에 대응하는 RTK 고정 위치해의 VPL은 Eq. (8)과 같이 산출된다.
$$VPL_{H_{0}}=\Phi^{-1}\!\left(1 – \frac{I_{H_{0},v} – \left( 1 – P_{CF}(Q_{\hat{N}}, Z) \right)}{2 P_{CF}(Q_{\hat{N}}, Z)}\right)\sigma_{\hat{v}}$$
여기서 $\sigma_{\hat{v}}$는 RTK 고정 위치해의 수직 방향 표준 편차를 의미한다. Eq. (8)을 기반으로 RTK 고정 위치해의 VPL을 산출하기 위해서는 $P_{CF}(Q_{\hat{N}}, Z)$값이 Eq. (9)의 부등식을 반드시 만족해야 한다.
$$1 – I_{H_{0},v} < P_{CF}(Q_{\hat{N}}, Z)$$
Eq. (9)의 조건을 만족하면 RTK 고정 위치해의 VPL 산출이 가능하고 경보 한계와 비교하여 가용성 평가가 가능하다. 그렇지 않을 경우, 고정 위치해의 보호수준을 산출할 수 없고 상대적으로 정확도가 낮은 실수 위치해( )의 VPL을 Eq. (10)과 같이 산출할 수 있다.
$$VPL_{H_{0}}=\Phi^{-1}\!\left( 1 – \frac{I_{H_{0},v}}{2} \right) \sigma_{\hat{v}}$$
여기서 $\sigma_{\hat{v}}$는 실수 위치해의 수직 방향 표준편차를 나타낸다. 이러한 시스템에서 고정 위치해의 가용률은 전체 에포크 중 Eq. (9)를 만족하여 고정 위치해를 사용할 수 있는 에포크의 비율을 의미하며, 미지정수 고정 과정에서 산출되는 $P_{CF}(Q_{\hat{N}}, Z)$값에 의존한다.
이번 장에서는 LAMBDA 기법에 구현된 기존 Z-행렬 탐색 알고리즘과, 이를 확장하여 탐색 영역 및 성능을 향상시키기 위한 후보군 생성 기법을 기술한다. 3.1절에서는 Teunissen (1995)에 제시된 기존 Z-행렬 탐색 알고리즘의 구조와 작동 원리를 설명하고, 3.2절에서는 본 연구에서 제안하는 Z-행렬 후보군 생성 알고리즘의 구성과 절차를 기술하였다.
Teunissen (1995)에 기술되어 있는 Z-행렬 탐색 알고리즘은 주어진 미지정수 실수해의 공분산 행렬을 입력값으로, 미지정수 간 상관관계를 최소화하고 P(CF) 값을 최대화하는 Z-행렬을 탐색한다. 이때, Z-변환된 실수해를 정수해로 고정하고 정수 성질을 유지하면서 원래 도메인으로 역변환해야 하므로, Z-행렬은 다음의 제약 조건을 모두 만족해야 한다.
1) 모든 성분이 정수로 구성되어야 한다
2) 미지정수의 수가 일 때 크기의 정방 행렬이어야 한다.
3) 행렬식의 절댓값이 1이어야 한다.
최종적으로 산출되는 P(CF) 값은 Z-변환 및 LDL 분해 이후 도출되는 D 행렬의 대각 성분이 작을수록 높게 산출된다. 위 조건을 만족하여 Z-변환 행렬의 행렬식이 ±1인 경우, 변환 전후의 실수해 공분산 행렬의 행렬식은 동일하게 유지된다. 이는 LDL 분해 시에도 동일하게 적용되어, 어떤 Z-행렬을 사용하더라도 D 행렬의 대각 성분 곱은 실수해 공분산 행렬의 행렬식과 같고 변하지 않는다. 이와 같이 D 행렬 대각 성분의 곱이 일정하게 유지되는 상황에서, P(CF)가 최대화되는 조건은 D 행렬의 대각 성분들이 모두 동일한 경우이다. 이 케이스는 Eq. (11)과 같이 표현할 수 있다.
$$
D^{*}_{11} = D^{*}_{22} = \cdots = D^{*}_{nn}
= \sqrt[n]{Q_{\hat{z}}},
\qquad
P^{*}_{CF}(Q_{\hat{N}}, Z^{*})
= \prod_{i=1}^{n}
\left( 2 \Phi\!\left( \frac{1}{2 \sqrt{D^{*}_{ii}}} \right) – 1 \right)
$$
여기서 $D^{*}$는 모든 대각 성분이 동일한 이상적인 D 행렬을 의미하며, $Z^{*}$는 해당 $D^{*}$를 생성하는 Z-변환 행렬을 나타낸다. $P^{*}_{CF}(Q_{\hat{N}}, Z^{*})$는 입력값인 미지정수 실수해 공분산 행렬 $Q_{\hat{N}}$에 대해 이론적으로 달성 가능한 P(CF)의 최대값을 나타낸다. 이론적으로는 위 조건을 만족하는 $Z^{*}$ 행렬을 역으로 계산하는 것이 가능하다. 하지만 미지정수 고정에 적용하기 위해서는 모든 성분이 정수이어야 하기 때문에 미지정수 고정 과정에 $Z^{*}$ 행렬을 적용할 수 없다. 따라서 기존 Z-행렬 탐색 알고리즘에서는, 정수 제약을 만족하면서도 D 행렬의 대각 성분들이 최대한 균일하게 분포하도록 하는 Z-행렬을 수치적으로 탐색한다.
기존 Z-행렬 탐색 알고리즘에서는 행 순서 재정렬(reordering) 및 정수 가우스 변환(integer Gauss transformation)의 조합을 통해 정수형 Z-행렬을 산출하였다 (Teunissen 1995). 일반적으로 Z-변환 전의 미지정수 실수해 공분산 행렬에 대해 LDL 분해를 수행하면, D 행렬의 대각 성분들 간에 심한 불균형이 존재하며, 특히 뒤쪽 성분일수록 상대적으로 큰 값을 가지는 경향이 나타난다 (Teunissen 1995). 이때 행 순서 재정렬을 통해 i번째와 i+1번째 성분의 순서를 교환하면, L 행렬에 포함된 두 성분 간 상관관계의 크기에 따라 D 행렬의 대각 성분들이 변경된다. 이러한 교환은 조건부 분산에 영향을 주며, 경우에 따라 i+1번째 성분의 D 값이 감소하여 전체 P(CF)의 향상으로 이어질 수 있다. Eq. (12)는 i번째와 i+1번째 성분을 교환했을 때 D 행렬 대각 성분의 변화를 정리한 결과를 나타낸다 (Teunissen 1995).
$$D’_{i:i+1} = \begin{bmatrix}
d’_{i} & 0 \\
0 & d’_{i+1}
\end{bmatrix}
=
\begin{bmatrix}
d_{i+1} – \dfrac{l_{i+1,i}^{2} d_{i}^{2} d_{i+1}}{\,d_{i} + l_{i+1,i}^{2} d_{i} d_{i+1}\,} & 0 \\
0 & d_{i} + l_{i+1,i}^{2} d_{i} d_{i+1}
\end{bmatrix}$$
여기서 $D’_{i:i+1}$는 순서 교환 이후 변환된 부분 행렬을 나타낸다. $d’_{i}$, $d’_{i+1}$은 순서 교환 이후 i번째 및 i+1번째 대각 성분을 의미하며, $d_{i}$, $d_{i+1}$은 변환 이전의 대각 성분이다. $l_{i+1,i}$는 변환 전 L 행렬의 성분이다. 위 수식에 따르면, 두 성분 간의 순서 교환 이후에도 두 성분의 곱은 Eq. (13)과 같이 동일하게 유지됨을 알 수 있다. 이는 앞서 설명한 바와 같이, Z-변환 이후에도 D 행렬의 대각 성분 곱이 불변함을 의미한다.
$$
d_{i} \times d_{i+1} = d’_{i} \times d’_{i+1}
$$
일반적으로 LDL 분해의 특성상, D 행렬의 뒤쪽 성분일수록 값이 더 크게 나타난다 (Teunissen 1995). 따라서 $l_{i+1,i}$의 값이 작을수록 $d’_{i+1}$값이 작아지게 되어, P(CF) 관점에서 이득을 극대화할 수 있다. 이러한 구조적 특성에 기반하여, Z-행렬 탐색 알고리즘에서는 L 행렬의 비대각 성분을 최소화하기 위해 순서 교환 이전에 정수 가우스 선형 변환을 수행한다 (Teunissen 1995). 기존 Z-행렬 탐색 알고리즘에서는 이러한 두 선형 변환의 조합을 반복적으로 수행하여 D 행렬 성분의 균일화를 수행하고 더 이상 순서 조정을 통해 이득을 볼 수 있는 경우가 존재하지 않으면 알고리즘을 종료한다 (Teunissen 1995). 이때 수행되었던 모든 정수 선형 변환 행렬의 곱의 형태로 Z-행렬이 정의되며, 총 t번의 순서 조정 이후 Z-행렬은 Eq. (14)와 같이 표현된다.
$$
Z = (\alpha_{t} \cdot \beta_{t}) \cdot (\alpha_{t-1} \cdot \beta_{t-1}) \cdot \ldots \cdot (\alpha_{2} \cdot \beta_{2}) \cdot (\alpha_{1} \cdot \beta_{1})
$$
여기서 $\alpha_{k}$, $\beta_{k}$는 각각 k-1번째 조정 이후 수행한 순서 재정렬 변환 및 정수 가우스 선형 변환 행렬을 나타낸다. 이때 각 선형 변환 행렬의 성분은 모두 정수이고 행렬식의 절댓값이 1이기 때문에 최종 산출되는 Z-행렬 또한 정수 제약 조건을 만족하게 된다.
기존 Z-행렬 탐색 알고리즘은 정수 가우스 변환과 순서 재정렬을 반복 수행한 뒤, 더 이상 개선 가능한 순서 교환이 존재하지 않으면 알고리즘을 종료한다 (Teunissen 1995). 하지만 이와 같은 종료 조건은 구조적으로 국소 최적해(local optimum)에 수렴할 가능성이 높아, 탐색되지 않은 더 우수한 Z-행렬이 존재하더라도 이를 탐색하지 못하는 한계가 있다.
이에 이 연구에서는 탐색 영역을 체계적으로 확장함으로써, 산출되는 Z-행렬의 최적성(optimality)을 개선할 수 있는 후보군 생성 기법을 제안한다. 제안된 기법은 기존 탐색 알고리즘 종료 이후, P(CF) 관점에서 의도적으로 손해를 감수하더라도 새로운 탐색 지점을 생성하고 결과적으로 더 나은 해를 발견할 가능성을 높이는 방향으로 설계되었다. 구체적인 알고리즘 구성은 다음과 같다.
미지정수의 수가 n개일 경우, 기존 알고리즘은 (1, 2), (2, 3), … , (n-1, n)의 순서 교환 쌍에 대해 P(CF)가 개선되지 않음을 확인한 시점에서 탐색을 종료하고 Z-행렬을 결정한다. 본 연구에서는 이 종료 조건 이후, n-1개의 교환에 대해 일시적으로 P(CF) 손해가 발생하더라도 강제로 순서 교환을 수행하고 새로운 n-1개의 탐색 지점을 생성한다.
예를 들어, (1, 2) 교환을 추가로 수행할 경우 새로운 초기 Z-행렬 $Z_{(1,2)}^{0}$가 설정되며, 이 경우 기존 알고리즘과 동일한 재탐색 절차를 통해 종료 조건을 만족하는 $Z_{(1,2)}^{f}$ 및 $P_{CF,(1,2)}$를 산출한다. 이를 n-1개의 순서 교환 쌍에 대해 반복 수행하면 Eq. (15)와 같이 총 n-1개의 Z-행렬 및 P(CF) 후보군이 생성된다.
$$
\left\{ Z^{f}_{(i,i+1)},\; P_{CF,(i,i+1)} \right\}_{i=1}^{\,n-1}
$$
위 후보군들 중에서 가장 큰 P(CF) 값을 가지는 해가 선택되며, 만약 해당 해가 기존 해보다 우수한 경우에는 이를 새로운 기준 해로 설정하고 동일한 후보군 생성 및 비교 절차를 반복 수행한다. 반대로, 더 이상 개선된 후보군이 존재하지 않으면 알고리즘은 종료된다. 위 절차를 통해, 본 알고리즘은 기존 종료 조건의 한계를 극복하고 더 높은 탐색 최적성을 달성할 수 있다. 이와 같은 반복적 구조를 통해 제안한 알고리즘은 기존 방법이 탐색하지 못했던 해를 추가로 고려함으로써, 전역 최적해(global optimum)에 도달할 가능성을 높일 수 있다. 특히 미지정수의 수가 많아서 공분산 행렬의 차원이 높은 환경에서는 더욱 효과적인 성능 향상이 기대된다. 다음 절에서는 RTK 항법 시뮬레이션 기반으로 제안하는 Z-행렬 후보군 생성 알고리즘의 성능 평가를 제시한다.
이번 장에서는 제안한 Z-행렬 후보군 생성 기법의 성능을 정량적으로 평가하기 위한 시뮬레이션 결과를 제시한다. 성능 평가는 기존 LAMBDA 기법 내 Z-행렬 탐색 알고리즘과의 비교를 통해 이루어지며, P(CF) 및 VPL 산출 결과를 중심으로 기법의 유효성을 검증한다.
이 연구에서는 제안한 Z-행렬 후보군 생성 기법의 성능을 정량적으로 평가하기 위해, Table 1에 요약된 파라미터를 기반으로 24시간 단일 에포크 RTK 시뮬레이션을 수행하였다. 단일 에포크 RTK는 각 에포크에서 수신된 GNSS 측정치에 최소자승 필터를 적용하여, 미지정수 실수해 및 실수 위치해를 산출하는 항법 시스템이다. 이중 위성군 이중 주파수 (GPS L1/L5, Galileo E1/E5) 환경에서 KAIST N 7-2 건물에 설치된 수신기 위치를 기준으로 GNSS 코드 및 반송파 측정치를 생성하였다. 시뮬레이션 간격은 1초로 설정하였으며, 24시간 동안 P(CF) 및 RTK 고정 위치해 산출을 통해 제안하는 기법의 성능을 평가하였다. 무결성 요구 조건은 ICAO (1996)에서 정의된 고신뢰 항법 시스템 기준에 따라 시간당 $10^{-7}$수준으로 설정하였다. 코드 및 반송파 GNSS 측정치의 멀티패스 오차 노이즈 수준은 Khanafseh et al. (2018)에서 제시한 도심 환경 멀티패스 오차 모델링 결과를 기반으로 설정하였다.
Table 1. Integrity requirements and sensor parameters.
| Parameter | Value | |
|---|---|---|
| Requirements | IH0, req | 10-7 / hour |
| Environments | Constellations | 24 GPS satellites / 24 Galileo satellites |
| Frequency | GPS: L1 & L5 Galileo: E1 & E5 | |
| Mask angle Simulation time Time interval Location σρ σϕ Time interval | 10 degrees 24 hours 1 seconds KAIST N 7-2 Bldg., Daejeon, South Korea 30 cm 6 mm 1 Hz | |
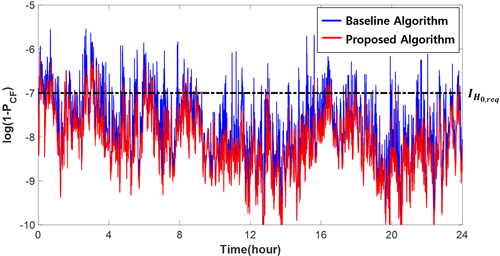
Fig. 1. Time series of log-scaled 1−P(CF) values over 24 hours. The red and blue lines represent results from the proposed and baseline Z-matrix search algorithms, respectively. The dashed line indicates the integrity requirement threshold of 10-7.
Fig. 2는 기존 Z-행렬 탐색 알고리즘(baseline algorithm)과 본 연구에서 제안한 Z-행렬 후보군 생성 알고리즘(proposed algorithm)을 적용하였을 때 VPL 산출 결과를 나타낸다. 각 에포크에서 산출된 P(CF) 값에 따라, 무결성 요구조건을 만족하는 경우에는 고정 위치해 VPL을, 만족하지 않는 경우에는 실수 위치해 VPL을 산출하여 각각 도시하였다. 각 그래프에서 검은색 선은 실수 위치해 VPL을, 파란색 선은 고정 위치해 VPL을 나타낸다. 추가적으로, 회색 선은 전체 에포크에서 산출한 실수 위치해 VPL을 예시로 나타낸 것이다. Table 2는 두 알고리즘의 P(CF), 고정 위치해 가용률, 그리고 VPL 평균값에 대한 정량적 비교 결과를 요약한 것으로, 제안 기법의 성능 향상을 보다 명확히 확인할 수 있다.
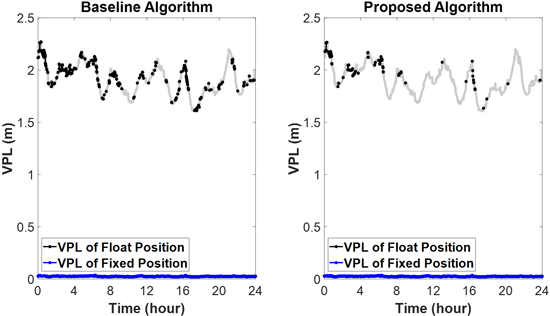
Fig. 2. VPL simulation results of float and fixed position solutions under nominal conditions. The left panel shows the results using the baseline algorithm, while the right panel presents those using the proposed Z-matrix candidate generation method. Improvements in P(CF) lead to higher availability of fixed solutions.
Table 2. Quantitative comparison between baseline and proposed Z-matrix search algorithms.
| Metric | Baseline algorithm | Proposed algorithm | Improvement |
|---|---|---|---|
| Mean 1-P(CF) Fixed position availability Mean fixed VPL Mean float VPL | 6.05×10−8 85.7% 2.47 cm 1.91 m | 2.17×10−8 95.3% 2.47 cm 1.91 m | 64.1% 9.6% – – |
제안한 Z-행렬 후보군 생성 기법을 적용함으로써 P(CF) 값이 기존 기법 대비 전반적으로 향상되었고, 이에 따라 고정 위치해 VPL의 가용률이 95.3%로 증가하였다. VPL 산출 시뮬레이션 결과, 실수 위치해 VPL의 평균값은 1.91 m로 나타났으며, 고정 위치해 VPL의 평균값은 약 2.47 cm로 매우 작게 나타났다. Reid et al. (2019)에서는 고성능 자율주행 항법시스템의 안정성 요구 조건으로 1.3 m의 VAL을 제시하였으며, 위 결과에 대하여 이를 만족하기 위해서는 고정 위치해 VPL 산출이 필수적임을 알 수 있다. 따라서, 제안한 기법을 통해 Z-행렬 성능과 P(CF) 값을 개선하고 고정 위치해의 가용률을 향상시키는 것은, 향후 RTK 항법 시스템의 높은 가용성 확보에 중요한 기여를 할 수 있을 것이다.
Fig. 3은 두 알고리즘을 적용하여 산출한 고정 위치해 VPL 결과를 비교한 것이다. 본 그래프는 Eq. (8)에 따라 산출된 고정 위치해 VPL의 시간 변화 양상을 나타내며, 해당 값은 고정 위치해의 수직 방향 표준편차와 P(CF)에 의해 결정된다. 시뮬레이션 결과, 기존 Z-행렬 탐색 알고리즘을 적용한 경우 일부 구간에서 고정 위치해 VPL 값에 비정상적으로 큰 분산이 나타나는 등, 국부적인 불안정성이 관측되었다. 반면, 제안한 후보군 생성 기법을 적용한 경우 VPL 값이 안정적으로 유지되는 양상을 보였다. 두 기법 모두 동일한 GNSS 측정치를 기반으로 하므로, 고정 위치해의 수직 방향 표준편차나 미지정수 실수해의 공분산 행렬에는 차이가 없다. 따라서 관측된 VPL 변화는 Z-행렬의 성능 차이에 기인한다고 해석할 수 있다. 이와 같은 결과는 기존 기법의 경우 탐색 종료 조건에 의해 비최적 Z-행렬이 산출되는 경우가 많아 VPL이 불안정하게 변동하는 반면, 제안 기법은 후보군 기반 탐색을 통해 보다 최적성이 높은 Z-행렬을 선택함으로써 VPL의 안정성과 신뢰도를 향상시킬 수 있음을 시사한다.
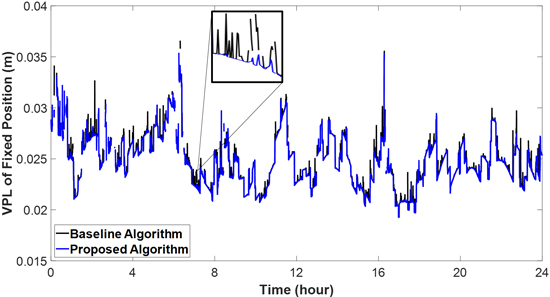
Fig. 3. Comparison of fixed-position VPL results between the baseline and proposed Z-matrix algorithms. The proposed method maintains more stable VPL values by generating Z-matrices with improved consistency and optimality.
본 연구에서는 RTK 항법 시스템의 미지정수 고정 과정에서 활용되는 Z-행렬의 성능을 개선하기 위해, Z-행렬 후보군 생성 기법을 제안하였다. 제안된 기법은 기존 탐색 알고리즘으로부터 산출된 Z-행렬에 대해 추가적인 선형 변환을 수행함으로써 후보군을 생성하고, 이 중 P(CF) 성능이 가장 우수한 Z-행렬을 선택함으로써 보다 최적화된 결과를 도출하는 방식이다. 24시간 단일 에포크 RTK 시뮬레이션을 통해 제안 기법의 성능을 정량적으로 평가한 결과, 전체 에포크의 97.5%에서 P(CF) 값이 향상되었으며, 1−P(CF)의 평균 개선폭은 64.1%로 나타났다. 그 결과, RTK 고정 위치해의 가용률은 기존 기법의 85.7%에서 제안 기법 적용 시 95.3%로 크게 개선되었다. 본 연구는 단일 에포크 기반의 간략화된 시뮬레이션 환경에서 제안 기법의 유효성을 검증하였으나, 해당 기법은 기존 칼만 필터 기반의 멀티 에포크 RTK 구조에도 적용 가능하다. 특히 Z-행렬 성능의 향상을 통해 미지정수 추정의 신뢰도가 개선되며, 결과적으로 RTK 시스템의 초기 수렴 시간 단축에도 기여할 수 있을 것으로 기대된다.
본 연구는 과학기술정보통신부의 재원으로 한국연구재단, 무인이동체미래선도핵심기술개발사업단의 지원을 받아 수행되었음 (No.2020M3C1C1A01086407).
Conceptualization, N. M.-C. Kim, methodology, N. M.-C. Kim, software, N. M.-C. Kim and D.-C. Min, validation, N. M.-C. Kim., D.-C. Min, and J.-Y. Lee, formal analysis, N. M.-C. Kim and D.-C. Min, investigation, N. M.-C. Kim., D.-C. Min, resources, N. M.-C. Kim., D.-C. Min, data curation, N. M.-C. Kim, writing—original draft preparation, N. M.-C. Kim., D.-C. Min, writing—review and editing, N. M.-C. Kim., D.-C. Min, visualization, N. M.-C. Kim, supervision, J.-Y. Lee, project administration, J.-Y. Lee, funding acquisition, J.-Y. Lee.
The authors declare no conflict of interest.
Enge, P. 1999, Local area augmentation of GPS for the precision approach of aircraft, Proceedings of the IEEE, 87, 111–132. https://doi.org/10.1109/5.736345
ICAO 1996, International Standards and Recommended Practices, Annex 10, July 1996. (Montreal: International Civil Aviation Organization).
Khanafseh, S., Kujur, B., Joerger, M., Walter, T., Pullen, S., et al. 2018, GNSS multipath error modeling for automotive applications, Proc. of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+), Miami, FL, 24–28 Sept. 2018, pp.1573–1589. https://doi.org/10.33012/2018.16107
Pervan, B. & Chan, F. C. 2001, System concepts for cycle ambiguity resolution and verification for aircraft carrier landings, Proc. of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS), Salt Lake City, UT, 11–14 Sept. 2001, pp.1228–1237. https://www.ion.org/publications/abstract.cfm?articleID=1801
Reid, T. G. R., Houts, S. E., Cammarata, R., Mills, G., Agarwal, S., et al. 2019, Localization requirements for autonomous vehicles, SAE Int. J. Connect. Autom. Veh., 2, 173–190. https://doi.org/10.4271/12-02-03-0012
Teunissen, P. J. G. 1995, The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation, J. Geodesy, 70, 65–82. https://doi.org/10.1007/BF00863419
Teunissen, P. J. G. 1998, Success probability of integer GPS ambiguity rounding and bootstrapping, J. Geodesy, 72, 606–612. https://doi.org/10.1007/s001900050199
Teunissen, P. J. G. 1999, An optimality property of the integer least-squares estimator, J. Geodesy, 73, 587–593. https://doi.org/10.1007/s001900050269