1Navigation/Weapon Data Link R&D (inertial navigation), LIG Nex1, Seongnam Gyeonggi-do 13488, Korea
2The 4th R&D Institute – The 6th Directorate, Agency for Defense Development, Daejeon 34060, Korea
†Corresponding Author: Hyun-Seup Cho, E-mail: hyunseup.cho@lignex1.com
Citation: Cho, H.-S., Ahn, T.-D., Moon, S.-C., Hwang, K.-H., Lee, T.-H., et al. 2025, A Constrained Optimization Framework for Camera Intrinsic Parameters Based on Camera-IMU Calibration, Journal of Positioning, Navigation, and Timing, 14, 231-239.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 231-239. https://doi.org/10.11003/JPNT.2025.14.3.231
Received on Aug 10, 2025, Revised on Aug 17, 2025, Accepted on Aug 23, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In aerial vision-based navigation systems, accurately estimating the misalignment between the camera and the inertial measurement unit (IMU) is critical. However, uncertainty in the camera’s intrinsic parameters can propagate to misalignment estimation and result in geometric errors. This can lead to significant degradation of vision-based navigation performance during high-altitude operations. To address this, we propose a reversal calibration method that leverages extrinsic parameters information to determine the effective range of intrinsic parameters. Based on the results of extrinsic calibration, we define an effective correction region for intrinsic parameters with respect to the physical centers of both sensors. This relationship is then integrated into a constrained optimization framework to refine the intrinsic parameters within physically valid bounds. Experiments were conducted using a camera with a focal length of 35 mm. The results demonstrate that incorporating physical constraints into the optimization process leads to more stable parameter correction, and reduced reprojection errors by up to 60.73%.
camera intrinsic parameters, constrained optimization, misalignment, Kalibr, lever-arm
항공기와 같은 이동체에서는 Global Positioning System (GPS)와 Inertial Navigation System (INS)를 결합한 복합항법 시스템을 통해 이동체의 위치와 자세를 추정한다. 하지만 전파 교란 (jamming)이나 스푸핑 (spoofing)과 같은 환경에서는 GPS의 신호 수신이 제한됨에 따라 복합 항법 시스템의 정상적인 운용이 불가능해지는 치명적인 한계가 존재한다. 이러한 한계를 보완하기 위해 최근에는 카메라로부터 얻어지는 영상을 기반으로 한 영상 기반 항법 (Vision-based Navigation)에 대한 연구가 활발히 진행되고 있다. 영상항법 시스템은 영상을 이용하는 방식에 따라 실시간 영상과 저장된 참조 영상을 매칭하여 위치를 추정하는 장면 매칭 항법 (Digital Scene Matching Area Correlation, DSMAC) (Carr & Sobek 1980), 연속된 영상 프레임 간의 특징점의 이동을 추적하여 상대적인 이동 거리와 방향을 추정하는 특징점 추적 항법 (Visual Odometry, VO) (Nistér et al. 2004), VO의 개념을 기반으로 IMU 데이터를 추가적으로 이용하며 자세를 보정하는 영상-관성 항법 시스템 (Visual-Inertial Navigation System, VINS) 등이 대표적인 방식이다 (Qin et al. 2018). 이로 인해 입력으로 사용되는 영상의 품질과 기하학적 정확도가 전체 영상 항법 시스템의 성능에 결정적인 영향을 미친다. 특히 카메라의 내부 파라미터 (intrinsic parameters)는 3차원 세계의 물체가 2차원 영상으로 투영되는 과정을 정의하며 이는 곧 카메라 좌표계와 세계 좌표계 간의 대응관계를 나타낸다. 이러한 내부 파라미터가 정확하게 보정되지 않을 경우 위치 추정과 지도 정합 과정에서 기하학적 오차를 발생시킨다. 이러한 현상은 항공기와 같이 고도가 높아질수록 더욱 두드러지는데 이는 동일한 내부 파라미터 오차가 지면 상의 물체 투영 위치에 더 큰 기하학적 오차를 유도하기 때문이다.
본 논문은 카메라 캘리브레이션을 위한 내부 파라미터 추정의 새로운 방식을 제안하며 다음과 같이 구성되었다. 2장에서는 카메라 캘리브레이션의 기존 연구를 소개하고 3장에서는 카메라 캘리브레이션을 위한 유효 범위 도출 및 제약조건 최적화 방법에 대해 소개한다. 4장에서는 실제 실험을 통해 얻어진 데이터 셋을 이용하여 기존 방식과 본 논문에서 제안하는 방식의 성능을 재투영 오차 (reprojection error) 값으로 비교한다. 마지막으로 5장에서는 결과를 요약하고 결론을 맺는다.
카메라 캘리브레이션은 컴퓨터 비전 및 영상항법 시스템에서 필수적인 전처리 과정으로 일반적으로 체커보드와 같은 패턴을 활용하여 내부 파라미터를 추정하는 과정을 말한다. 대표적으로 Zhang (2000)은 3D 기준점을 이용하는 대신 2D 평면상의 체커보드 패턴을 이용하여 각 영상에서 2D 호모그래피 행렬을 추정하였다. 각 영상에서 추정된 호모그래피 행렬은 비선형 Maximum Likelihood Estimation (MLE) 함수의 최적화를 위한 초기값으로 활용되는 방식이 제안되었다. 이후 이러한 방식은 대표적인 컴퓨터 비전 오픈소스 라이브러리인 OpenCV와 MATLAB 등에서 구현되어 카메라 캘리브레이션을 위한 대표적인 표준방식으로 사용되고 있다. 이러한 방식과 유사하면서 대표적인 선행 연구로는 Tsai (2003)와 Heikkilä & Silvén (1997)가 존재한다. 두 방식 모두 핀홀 카메라 모델을 사용한다는 점에서 동일하지만 렌즈의 왜곡 계수를 다르게 표현한다는 점에 있어 차이점을 가진다 (Sun & Cooperstock 2006). Tsai (2003)는 영상 좌표 기반의 방사 왜곡 (radial distortion) 모델과 2단계 선형 추정 구조를 사용하여 간단한 구조를 가지는 보정 방식을 제안하였다. 반면, Heikkilä & Silvén (1997)은 방사 및 접선 왜곡까지 포함하는 확장된 렌즈 왜곡 모델을 활용함과 동시에 Direct Linear Transformation (DLT)를 이용하여 카메라의 자세를 구한 뒤 내부 파라미터를 순차적으로 최적화하는 방식을 제안하였다.
방사형 왜곡 (radial distortion)을 보다 정밀하게 모델링하거나 변형하는 방식도 다수 연구되어 왔다. Ma et al. (2006)은 기존의 다항식 기반 왜곡 보정법이 저품질 렌즈나 심한 비선형 왜곡 환경 문제가 있음을 제기하고 piecewise 모델을 제안하였다. 이 모델은 픽셀 반경의 길이를 기준으로 왜곡을 표현하는 함수를 2개의 구간으로 나누어 고도화하는 방식이다. Hartley & Kang (2007)은 방사 왜곡 모델의 계수를 사전 정의하지 않고 정규화된 좌표계에서 직접 추정하는 방법을 제안하였으며 방사 왜곡 중심을 주점과 별개로 추정하여 함으로써 기존 다항식 기반의 모델보다 더 높은 보정 성능을 얻었다. 마지막으로 Zhou et al. (2020)은 Unmanned Aerial Vehicle 기반 항공사진 촬영에서 카메라 내부 파라미터의 보정 오류가 3차원 재구성과 자세 추정에 미치는 영향을 시뮬레이션을 통하여 분석하였다. 특히 내부 파라미터 중 초점 거리의 잘못된 초기값을 선정할 경우 누적 오차로 이어진다는 점을 통해 정확한 카메라 캘리브레이션은 높은 신뢰성과 정밀도를 확보하는데 필수적이다.
본 논문에서는 Kalibr (ETH Zurich Autonomous Systems Lab 2022)을 활용하여 카메라-IMU 간의 외부 파라미터 값을 기반으로 제약조건을 구성하여 내부 파라미터를 재보정하는 새로운 방식을 제안한다. 이에 대한 전체 다이어그램은 Fig. 1에 시각적으로 나타내었다. 가장 먼저 카메라에서 얻어진 체커보드 영상을 이용하여 Camera Calibrator App (CCA)으로 내부 파라미터를 추정한다. 이후 Kalibr에서 외부 파라미터 정보를 얻기 위해 별도의 April Grid 영상 (Olson 2011)과 Inertial Measurement Unit (IMU) 데이터를 활용하여 결과를 획득한다. 특히 Kalibr을 수행할 때는 앞서 CCA를 통해 얻어진 내부 파라미터 값을 다양하게 조정하면서 이 값이 외부 파라미터 추정 결과에 미치는 영향을 실험적으로 분석하였다. 실험 결과 주점의 변화는 X, Y축, 초점의 변화는 Z축 레버암과 선형적인 관계를 가지고 있음을 확인하였다. 이와 동시에 실제 도면 상에서 레버암의 유효한 범위를 물리적으로 측정하였을 때 CCA에서 추정된 내부 파라미터는 이 유효 범위를 역으로 이용하여 카메라 캘리브레이션을 위한 부등식 제약조건으로 구성될 수 있다.
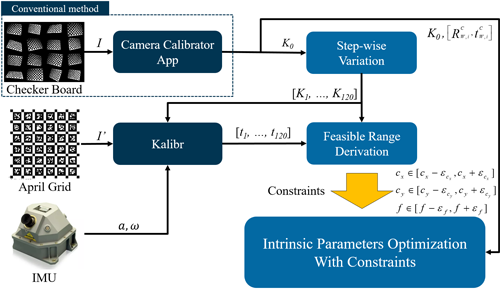
Fig. 1. Overall block diagram of the proposed approach in detail.
Kalibr은 카메라의 재투영 오차와 IMU의 가속도/각속도 오차를 동시에 최소화하는 비선형 최적화 기반 프레임워크로 카메라-IMU 간 위치 및 자세 관계, 즉 외부 파라미터 값을 추정하는 대표적인 오픈소스 도구이다 (Rehder et al. 2016). 이러한 최적화 과정에서 Kalibr은 카메라 내부 파라미터 외에도 IMU의 동적 특성인 잡음 noise density와 바이어스 랜덤워크 (bias random walk)에 대한 사전 정보가 필수적으로 입력되어야 한다. IMU의 경우, 대부분 제조사에서 제공하는 데이터 시트를 통하여 입력에 필요한 동적 특성 값을 비교적 쉽게 얻을 수 있는데 반해, 카메라 내부 파라미터의 경우 영상을 획득한 시점의 렌즈 세팅, 조도 환경 등에 따라 값이 상이하므로 툴을 이용하여 직접 카메라를 보정하는 것이 필수적이다. 특히 초점거리나 주점 위치의 미세한 차이가 외부 파라미터 추정에 큰 영향을 줄 수 있기 때문에 신뢰할 수 있는 내부 파라미터가 외부 파라미터 추정에 있어 중요한 요소로 작용한다.
가장 먼저 카메라에 대한 내부 파라미터를 획득하기 위해 MATLAB에서 제공하는 CCA를 활용하였다. CCA는 체커보드 영상을 이용하여 카메라의 초점거리, 주점, 왜곡 계수 등의 여러 내부 파라미터를 동시에 추정할 수 있다. 그러나 선택된 영상의 개수, 촬영된 거리 및 각도에 따라 내부 파라미터의 표준 편차가 크게 나타나는 경향을 보이기 때문에 신뢰성에 대한 문제점이 존재한다. 이러한 문제를 해결하기 위해 추정된 내부 파라미터 값이 카메라-IMU 간의 외부 파라미터에 미치는 영향을 분석하였다. 앞서 CCA에서 얻어진 내부 파라미터를 기준 값으로 설정한 후 $x$축 주점 $c_x$, $y$축 주점 $c_y$, 초점 거리 $f$를 각각 ±5 픽셀 간격으로 최대 ±100 픽셀까지 인위적으로 변화시켜 총 120개의 변경된 내부 파라미터 조합을 생성하였다. 이후 Figs. 2a,b와 같은 환경에서 카메라-IMU 데이터를 획득한 후 생성된 내부 파라미터 조합을 입력하여 Kalibr을 실행했을 때 마찬가지로 120개의 외부 파라미터 결과를 얻을 수 있다. 이때 3개의 내부 파라미터 변화가 6-자유도로 표현되는 외부 파라미터에 미치는 영향은 Fig. 3에 표현하였다. Figs. 3a,b,c는 각각 $c_x$, $c_y$, $f$를 변화 시켰을 때 외부 파라미터가 변화하는 결과를 나타내며 빨간색 직선은 1차 선형 회귀 결과를 나타낸다. 여기서 6-자유도 외부 파라미터는 각각 $x$축 방향 레버암 $t_x$, $y$축 방향 레버암 $t_y$, $z$축 방향 레버암 $t_z$, roll 각도 $\phi$, pitch 각도 $\theta$, yaw 각도 $\psi$로 나타내었다. Table 1에 나타낸 바와 같이 내부 파라미터의 변화는 회전 성분($\phi,\theta,\psi$)에는 영향을 미치지 않는 반면 레버암 성분($t_x, t_y, t_z$)에는 큰 영향을 주는 것으로 나타났고, 이때의 $c_x – t_x,\; c_y – t_y,\; f – t_z$ 간의 결정 계수(R-Squared)를 계산결과는 각각 0.9980, 1.0000, 1.0000으로 나타났다. 따라서 고정된 위치에서 특정 치구에 장착된 카메라와 IMU 간의 레버암은 변하지 않는 상수 값이라고 가정했을 때 이러한 결과는 Eq. (1)과 같이 간단한 선형 모델로 표현할 수 있다.
$$\begin{bmatrix}
t_x \\
t_y \\
t_z
\end{bmatrix}
=
\begin{bmatrix}
a_1 & a_2 & a_3 \\
a_4 & a_5 & a_6 \\
a_7 & a_8 & a_9
\end{bmatrix}
\begin{bmatrix}
c_x \\
c_y \\
f
\end{bmatrix}
+
\begin{bmatrix}
b_1 \\
b_2 \\
b_3
\end{bmatrix}$$
여기서 $A$는 변화율을 나타내는 행렬, $B$는 바이어스를 나타내는 벡터이다. Table 1에서 나타내었듯이 $A$의 대각 성분을 제외한 나머지 항들은 대부분 0에 가까운 근사치로 수렴한다. 따라서 각 내부 파라미터의 변화는 특정한 축 방향의 레버암에만 영향을 미친다. 이로 인하여 $A$는 대각 행렬이면서 동시에 선형 독립 특성을 가지고 있기 때문에 ±100 픽셀 범위 내에서 $A$는 non-singular임을 보장할 수 있고 역행렬인 $A^{-1}$가 항상 존재한다.
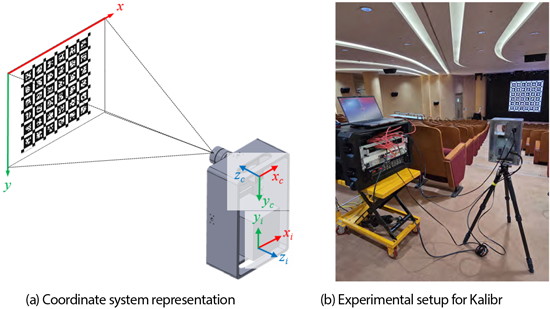
Fig. 2. Experimental setup for obtaining camera-IMU extrinsic parameter using Kalibr.
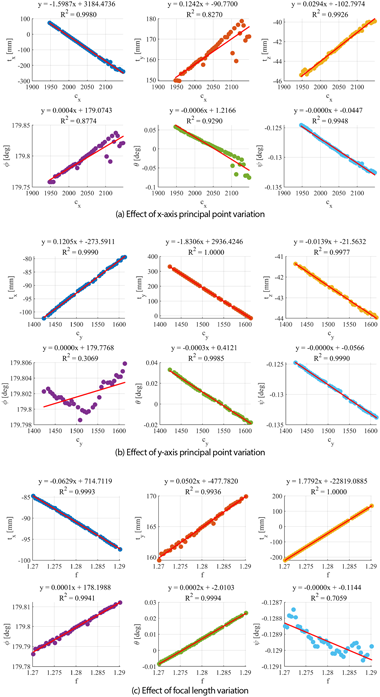
Fig. 3. Relationship between intrinsic parameters and the extrinsic parameters, along with the linear regression results.
Table 1. Regression coefficients representing the relationship between intrinsic parameters and extrinsic parameters.
| tx [mm] | ty [mm] | tz [mm] | φ [deg] | θ [deg] | ψ [deg] | |
|---|---|---|---|---|---|---|
| cx [px] | -1.5987 | 0.1242 | 0.0294 | 0.0004 | -0.0006 | 0.0000 |
| cy [px] | 0.1205 | -1.8306 | -0.0139 | 0.0000 | -0.0003 | 0.0000 |
| f [px] | -0.0629 | 0.0502 | 1.7792 | 0.0001 | 0.0002 | 0.0000 |
$A$의 대각 성분을 제외한 모든 성분을 0으로 가정하고 카메라-IMU 간의 물리적으로 유효한 레버암의 범위를 설정하기 위해 허용 오차 벡터 $[\varepsilon_x,\, \varepsilon_y,\, \varepsilon_z]^{T}$를 추가하면 역으로 카메라 내부 파라미터의 유효 범위를 Eq. (2)와 같이 결정할 수 있다.
$$\begin{bmatrix}
c_x \pm \varepsilon_{c_x} \\
c_y \pm \varepsilon_{c_y} \\
f \pm \varepsilon_{f}
\end{bmatrix}
=
\begin{bmatrix}
a_1 & 0 & 0 \\
0 & a_5 & 0 \\
0 & 0 & a_9
\end{bmatrix}^{-1}
\left(
\begin{bmatrix}
t_x \pm \varepsilon_x \\
t_y \pm \varepsilon_y \\
t_z \pm \varepsilon_z
\end{bmatrix}
–
\begin{bmatrix}
b_1 \\
b_2 \\
b_3
\end{bmatrix}
\right)$$
여기서 $t_x, t_y$는 Fig. 4a와 같이 카메라의 주점 포인트와 IMU의 Computational Center (CC) 간의 거리로 나타내어지므로 도면 상에서 쉽게 거리를 측정할 수 있다. 하지만, $t_z$는 Fig. 4b에서 나타낸 바와 같이 카메라 렌즈 내부의 광학 중심 (optical center)과 IMU CC 사이의 높이 차를 나타내므로 실제 물리적인 위치를 외부에서 정확히 특정하기 어렵다. 그러나 초점 거리는 이미지 센서의 중점인 광학 중심에서 영상 센서까지의 거리로 정의되므로 카메라의 도면상 렌즈 구조가 제공되는 경우 $t_z$를 대략적으로 추정할 수 있다. 본 논문에서는 카메라 제조사에서 제공하는 도면을 활용하여 광학 중심의 위치를 설정하고 전체 레버암 벡터 $([\,t_x,\, t_y,\, t_z\,]^T = [-89.98\,\mathrm{mm},\; 162.5\,\mathrm{mm},\; -48.5\,\mathrm{mm}]^T)$를 구성하였다.
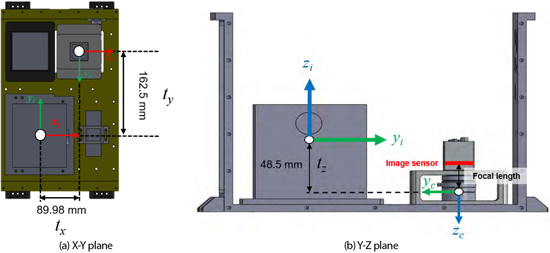
Fig. 4. Measurement results illustrating the lever arm between the camera and IMU on the system layout diagram.
$\varepsilon = [\,\varepsilon_x,\; \varepsilon_y,\; \varepsilon_z\,]^T$의 값을 설정하기 위해서는 실제 센서 시스템에서 발생할 수 있는 다양한 오차 요소가 고려되어야 한다. 주요 요인으로는 센서 장착 오차, 구조적 공차 등이 대표적으로 존재한다. 하지만 다양한 불확실성 요소를 식별하고 반영하기 위해서는 명백한 한계가 존재한다. 이를 감안하였을 때 영상의 주점과 IMU의 $X$, $Y$축 CC로 결정되는 $t_x$,$t_y$는 대부분 고정된 위치에서 작은 편차를 가지기 때문에 $\varepsilon_x, \varepsilon_y$는 10 mm로 설정하였다. 반면, $\varepsilon_x$의 경우 카메라의 초점을 조절함으로써 큰 편차를 가질 수 있기 때문에 $X$, $Y$축 허용오차 보다 2배 큰 값인 20 mm로 설정하였고, 이후 적절한$\varepsilon$ 값을 설정하기 위해 추가적인 실험을 진행하였다. 결론적으로 적절한 $\varepsilon$ 값을 결정되었을 때 Eq. (2)를 활용하면 역으로 내부 파라미터의 허용오차 ($\left[\, \varepsilon_{c_x},\; \varepsilon_{c_y},\; \varepsilon_f \,\right]^{T}$)를 결정할 수 있다. CCA 등을 이용하여 추정된 카메라 내부 파라미터는 이 범위 내에서 추정된 경우에만 의미 있는 결과로 해석될 수 있을 뿐만 아니라 추후 내부 파라미터 재보정을 위한 제약 조건으로도 활용될 수 있다.
이번절에서는 3.2절에서 도출된 카메라 내부 파라미터의 유효 범위를 기반으로 제약조건 기반 최적화 문제의 구성 방법을 구체적으로 설명한다. 설계 변수에 대한 초기값의 설정은 Zhang (2000)의 방식처럼 호모그래피 행렬을 계산하는 것이 아닌 CCA를 통해 얻어진 초기 내부 파라미터($K_0$)와 체커보드에서 카메라 좌표계로의 변환 관계를 나타내는 외부 파라미터 ($[R_{w,i}^c,t_{w,i}^c ]$)를 다시 한번 최적화하는 것을 목표로 하였다. 여기서 외부 파라미터는 Rodrigues 벡터 형식의 3차원 회전 요소와 3개의 레버암 요소로 구성되며 각 영상의 인덱스 $i$마다 독립적으로 추정된다. 따라서 전체 영상의 수를 $N$이라 할 때, 외부 파라미터와 관련된 설계 변수의 개수는 총 $6N$개가 된다. 여기에 모든 영상에서 공통적으로 적용되는 내부 파라미터와 왜곡 계수를 포함하면 내부 파라미터 재최적화를 위한 전체 설계 변수의 개수는 $6N+5$개로 Eq. (3)과 같이 표현된다.
$$x = [\,
r_{1,1},\ r_{2,1},\ r_{3,1},\ \ldots,\
r_{1,N},\ r_{2,N},\ r_{3,N},\
t_{x,1},\ t_{y,1},\ t_{z,1},\ \ldots,\
t_{x,N},\ t_{y,N},\ t_{z,N},\
k_{1},\ k_{2},\ c_{x},\ c_{y},\ f
\,]$$
여기서 [$r_1, r_2, r_3$]은 Rodrigues 회전 요소, [$t_x, t_y, t_z$]는 각 축에 대응하는 레버암, $k_1, k_2$는 방사형 왜곡 계수, $c_x, c_y, f$는 카메라 내부 파라미터를 나타낸다. 이때의 내부 파라미터의 유효 범위를 고려한 비선형 최적화 문제는 Eq. (4)와 같이 재투영 오차를 최소화하는 방식으로 정의하였다.
$$\min\left(
\sum_{i=1}^{N}
\sum_{j=1}^{M}
\left\| p_{j}
– K \cdot h\!\left( R_{w,i}^{c} P_{w,j} + t_{w,i}^{c} \right)
\right\|^{2}
\right) \\ \text{Subject to } \;
c_x \in
\left[
c_x – \varepsilon_{c_x},\;
c_x + \varepsilon_{c_x}
\right] \\ c_y \in \left[\, c_y – \varepsilon_{c_y},\; c_y + \varepsilon_{c_y} \right] \\ f \in \left[\, f – \varepsilon_{f},\; f + \varepsilon_{f} \right]$$
여기서 아랫 첨자$j$는 영상 1장에 존재하는 특징점의 개수를 의미하며, $p$는 영상에서 추출된 2D 특징점, $P_w$는 체커보드에서 검출되는 3D 특징점을 의미한다. 또한, 비선형 함수 $h(\cdot)$는 방사형 왜곡을 보정하기 위한 함수로 왜곡되지 않은 정규화 영상 좌표를 입력 받아 왜곡된 영상 평면상의 위치를 Eq. (5)와 같이 계산한다.
$$h(\cdot)
=
\left(1 + k_{1} r^{2} + k_{2} r^{4}\right)
\begin{bmatrix}
\dfrac{X_{c}}{Z_{c}} \\
\dfrac{Y_{c}}{Z_{c}}
\end{bmatrix},
\; \text{where} \;
r = \sqrt{
\left( \frac{X_{c}}{Z_{c}} \right)^{2}
+
\left( \frac{Y_{c}}{Z_{c}} \right)^{2}
}$$
여기서 $[X_c,Y_c,Z_c]^T$는 각각 카메라 좌표계에서 정의된 3차원 좌표, 정규화된 이미지 평면 상의 점은 $[X_c/Z_c/Y_c/Z_c ]^T$, $r$은 영상 중점으로부터 정규화된 거리를 나타낸다. Eq. (4)의 전체 최적화 과정은 Levenberg-Marquardt (LM) 알고리즘을 이용하여 진행하였으며 만약 초기 내부 파라미터가 설정된 제약조건 범위를 벗어나는 경우를 방지하기 위해 전체 설계 변수 중 내부 파라미터에 대해서만 Eq. (6)과 같이 전처리 과정을 추가하였다.
$$[\, c_x,\ c_y,\ f \,] = x’ =
\begin{cases}
l, & \text{if } x’ < l, \\
x’, & \text{if } l \le x’ \le u, \\
u, & \text{otherwise}.
\end{cases}$$
여기서 $l$은 하한 값, $u$는 상한 값을 의미한다. 이를 통해 초기값이 상한 또는 하한을 초과하는 경우 자동으로 허용 범위 내 값으로 조정하여 제약조건을 위반하지 않도록 하였다.
이번 장에서는 카메라 캘리브레이션을 위한 실험 데이터셋의 구성과 수집 방법을 소개하고 이를 바탕으로 수행된 실험 결과를 제시한다. 실험은 Eq. (7)의 렌즈 방정식에 의해 카메라가 센서 평면에 적절하게 상이 맺힐 수 있는 거리를 고려하였다.
$$d_i = \frac{f \cdot d_o}{d_o – f}$$
여기서 $d_o$는 물체와 렌즈 사이 거리, $d_i$는 상이 맺히는 이미지 센서까지의 거리를 의미한다. 일반적으로 $d_o \gg f$인 경우, 영상 거리는 $d_i \approx f$로 근사할 수 있다. 본 논문에서는 $f = 35 mm$를 이용하여 실험을 진행하고 $d_o$는 실험 공간의 물리적 제약을 고려하였을 때 Fig. 5와 같이 체커보드 영상으로부터 15 m와 20 m 만큼 떨어진 위치 6곳을 선정하였다. 이에 따라 $d_i$는 거리가 15 m일 경우 35.06, 20 m일 경우 35.08 mm로 계산되어 $d_i \approx f$ 조건을 만족하는 위치에서 데이터를 획득할 수 있도록 하였다. 또한, 카메라 캘리브레이션을 위한 영상을 획득할 때 Fig. 6에서 표현한 바와 같이 단순한 정면뿐만 아니라 약 45도 정도의 기울인 자세를 추가하여 다양한 시점의 체커보드 영상이 데이터 셋에 포함될 수 있도록 하였다. 데이터 셋을 획득하기 위한 카메라의 특성, 타켓 패턴, 각 위치마다 얻은 영상의 개수는 Table 2에 정리하였고 Position은 각 영상이 촬영된 카메라의 위치를 나타낸다.
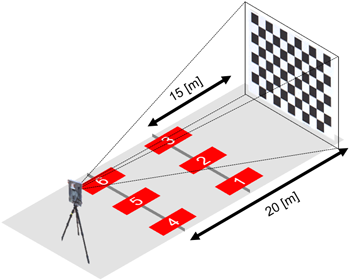
Fig. 5. Configuration of acquisition location and distances for the camera calibration.
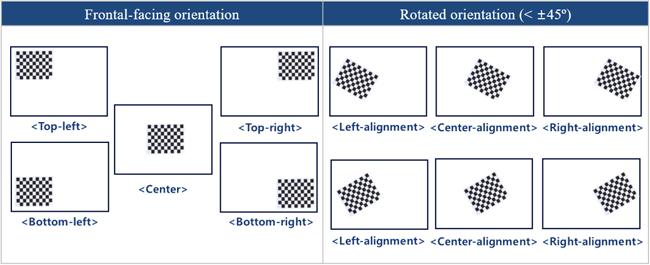
Fig. 6. Image acquisition method for camera calibration dataset configuration, which includes both frontal and tilted (approximately 45 degree) camera views.
Table 2. Camera specifications, target patterns, and number of images per location for camera calibration.
| Pos. | Camera specifications | Target patterns | Distance [m] | # of images |
|---|---|---|---|---|
| 1 2 3 4 5 6 | Width: 4096 Height: 3000 Focal length: 35 [mm] Pixel size: 2.74 [μm] | Square size: 335 [mm] Type: Checkerboard Rows: 7 Cols: 5 | 15 15 15 20 20 20 | 691 551 602 223 170 509 |
앞서 설정된 레버암 허용오차 벡터($\varepsilon = [\,\varepsilon_x,\ \varepsilon_y,\ \varepsilon_z\,]^{T}$)의 경우 유효한 내부 파라미터의 범위를 직접적으로 결정하기 때문에 추가적으로 다음과 같은 3가지의 케이스를 고려하여 내부 파라미터 재 최적화 과정에 미치는 영향성을 확인하였다.
1) ε=[10 mm, 10 mm, 20 mm]T
2) 0.5ε=[5 mm, 5 mm, 10 mm]T
3) 2ε=[20 mm, 20 mm, 40 mm]T
레버암 허용오차 벡터의 3가지 케이스에 따른 내부 파라미터의 유효 범위는 Table 3에 나타내었다. 3가지 케이스 중 모든 데이터셋에 대한 평균 재투영 오차를 측정한 결과 $2\varepsilon$ 일 때 가장 낮은 값을 보였고, CCA에서 얻어진 초기 내부 파라미터 결과 (Init)와 이에 대한 최적화 결과 (Opt)는 Table 4에 나타내었다. 실험 결과 초점거리 $f$에 대해 Init에서 추정된 값은 최소 12720.85에서 최대 13768.59까지 분포하며 표준편차가 373.83으로 계산되어 불확실성이 높은 것으로 나타났다. 반면 Opt에서 추정된 $f$ 값은 최소 12805.77부터 최대 12820.82까지 분포한다. 특히 12820.82 경우 상한 바운드 값과 일치하므로 제약조건이 활성화되어 $f$ 값의 추정에 직접적인 영향을 미치고 있음을 알 수 있다. 또한 Table 5에서 나타낸 바와 같이 제안한 방식이 대부분의 데이터 셋에서 제약조건을 효과적으로 활용함으로써 재투영 오차를 전반적으로 감소시키는 효과를 보였다. 특히, Position 6에서는 재투영 오차가 기존 방식 대비 60.84% 만큼 개선되어 가장 큰 개선 효과를 보였다. 하지만, Position 5에서는 예외적으로 2.63% 만큼 증가하였는데 무엇보다도 왜곡 계수 $k_1$이 다른 데이터셋과 비교하여 가장 크게 추정되었다. 이는 전체 설계변수에 걸쳐 $k_1$이 왜곡 보정 방향에 큰 영향을 주었기 때문으로 해석된다.
Table 3. Range of intrinsic parameters based on lever arm tolerance vectors.
| 0.5ε | ε | 2ε | |
|---|---|---|---|
| cx | [2045.08, 2051.33] | [2041.95, 2054.46] | [2035.69, 2060.7154] |
| cy | [1512.56, 1518.03] | [1509.83, 1520.75] | [1504.37, 1526.22] |
| f | [12792.71, 12803.96] | [12787.09, 12809.57] | [12775.85, 12820.81] |
Table 4. Comparison of initial parameters from camera calibrator app and optimized parameters using the proposed method, along with their standard deviation values.
| Position | cx [px] | cy [px] | f [px] | k₁ | k₂ | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Init | Opt (2ε) | Init | Opt (2ε) | Init | Opt (2ε) | Init | Opt (2ε) | Init | Opt (2ε) | |
| 1 | 2083.53 | 2060.72 | 1527.53 | 1526.22 | 12720.85 | 12789.42 | -0.011 | -0.010 | 0.438 | 0.535 |
| 2 | 2033.46 | 2035.70 | 1537.28 | 1525.54 | 12965.60 | 12820.82 | 0.003 | -0.003 | 0.288 | 0.340 |
| 3 | 2075.88 | 2036.52 | 1502.08 | 1504.40 | 12998.50 | 12820.82 | 0.002 | -0.005 | 0.441 | 0.366 |
| 4 | 2108.36 | 2040.68 | 1476.93 | 1504.37 | 12926.54 | 12820.82 | 0.003 | 0.001 | 0.238 | 0.182 |
| 5 | 2037.24 | 2052.59 | 1544.40 | 1526.17 | 13768.59 | 12820.82 | 0.041 | -0.103 | 0.197 | 0.197 |
| 6 | 2088.44 | 2046.82 | 1554.48 | 1526.22 | 12825.23 | 12820.82 | 0.007 | -0.002 | 0.423 | 0.296 |
| STD | 29.76 | 9.83 | 29.09 | 11.18 | 373.83 | 12.82 | 0.02 | 0.01 | 0.21 | 0.13 |
Table 5. Comparison of reprojection errors and reduction rates. Best reprojection error results are highlighted in bold.
| Position | Init | 0.5ε | ε | 2ε | |||
|---|---|---|---|---|---|---|---|
| Error [px] | Error [px] | Rates [%] | Error [px] | Rates [%] | Error [px] | Rates [%] | |
| 1 | 0.2231 | 0.2094 | 6.14 | 0.2093 | 6.19 | 0.2090 | 6.32 |
| 2 | 0.2269 | 0.2241 | 1.24 | 0.2239 | 1.32 | 0.2238 | 1.37 |
| 3 | 0.2444 | 0.2195 | 10.19 | 0.2191 | 10.35 | 0.2186 | 10.56 |
| 4 | 0.3513 | 0.2067 | 41.16 | 0.2054 | 41.53 | 0.2036 | 42.04 |
| 5 | 0.1896 | 0.1938 | -2.22 | 0.1952 | -2.95 | 0.1946 | -2.63 |
| 6 | 0.6081 | 0.2391 | 60.68 | 0.2387 | 60.73 | 0.2381 | 60.84 |
본 논문에서는 카메라-IMU 캘리브레이션 도구인 Kalibr을 통해 얻은 외부 파라미터 정보를 활용하여 카메라 내부 파라미터의 물리적으로 유효한 범위를 도출하고 이를 바탕으로 제약조건 기반 비선형 최적화 방식을 제안하였다. 기존의 카메라 캘리브레이션 방법은 영상 데이터와 환경에 따라 내부 파라미터 추정 값이 데이터 획득 환경에 따라 불확실성이 크다는 한계가 있는 반면, 본 논문에서 제안한 방식은 초점 거리, 주점의 변화가 레버암에 미치는 영향을 분석함으로써 실제 센서 시스템의 특성을 반영한 유효 범위를 설정하였다. 실험 결과 제안된 방식은 대부분의 데이터 셋에서 재투영 오차를 효과적으로 감소시켰지만 예외적으로 발생된 왜곡 계수의 영향은 영상에 대한 전처리 과정을 추가함으로써 개선될 것으로 기대된다. 더 나아가 Kalibr을 통해 추정되는 레버암은 모두 센서의 물리적 특성으로부터 결정되므로 이를 활용한다면 본 논문에서 제안한 접근법은 특정 장비나 환경에 관계없이 카메라-IMU 시스템에 일관적으로 적용될 수 있다.
이 논문은 2025년 정부의 재원으로 수행된 연구 결과임.
Conceptualization, H. Cho, T. Ahn, S. Moon and K. Hwang; methodology, H. Cho, S. Moon, K. Hwang and T. Lee; software, H. Cho, K. Hwang and T. Lee; validation, S. Moon and H. Hong; formal analysis, S. Moon and H. Hong; investigation, H. Cho, T. Ahn, S. Moon, K. Hwang, T. Lee and H. Hong; resources, H. Cho, T. Ahn, S. Moon, K. Hwang, T. Lee and H. Hong; data curation, H. Cho and K. Hwang; writing—original draft preparation, H. Cho, S. Moon, K. Hwang; writing—review and editing, S. Moon and H. Hong; visualization, H. Cho and K. Hwang and T. Lee; supervision, T. Ahn, S. Moon, J. Oh. and C. Sung; project administration, S. Moon, J. Oh and C. Sung; funding acquisition, J. Oh and C. Sung.
The authors declare no conflict of interest.
Carr, J. R. & Sobek, J. S. 1980, Digital scene matching area correlator (DSMAC), Proc. SPIE 0238, Image Processing for Missile Guidance, San Diego, United States, 23 December 1980, pp.36-41. https://doi.org/10.1117/12.959130
ETH Zurich Autonomous Systems Lab, Calibration Targets – Kalibr Wiki, 2022, [Internet], Cited 2022 Apr 28, available from: https://github.com/ethz-asl/kalibr/wiki/calibration-targets
Hartley, R. & Kang, S. B. 2007, Parameter-free radial distortion correction with center of distortion estimation, IEEE Transactions on Pattern Analysis and Machine Intelligence, 29, 1309-1321. https://doi.org/10.1109/TPAMI.2007.1147
Heikkilä, J. & Silvén, O. 1997, A four-step camera calibration procedure with implicit image correction, in Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17-19 June 1997, pp.1106-1112. https://doi.org/10.1109/CVPR.1997.609468
Ma, L., Chen, Y., & Moore, K. L. 2006, Analytical piecewise radial distortion model for precision camera calibration, IEE Proceedings – Vision, Image and Signal Processing, 153, 468-474. https://doi.org/10.48550/arXiv.cs/0307051
Nistér, D., Naroditsky, O., & Bergen, J. 2004, Visual odometry, in Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2004), Washington, DC, USA, 27 June 2004 – 02 July 2004. https://doi.org/10.1109/CVPR.2004.1315094
Olson, E. 2011, AprilTag: A robust and flexible visual fiducial system, in 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 09-13 May 2011, pp.3400-3407. https://doi.org/10.1109/ICRA.2011.5979561
Qin, T., Li, P., & Shen, S. 2018, VINS-Mono: A robust and versatile monocular visual-inertial state estimator, IEEE Transactions on Robotics, 34, 1004-1020. https://doi.org/10.1109/TRO.2018.2853729
Rehder, J., Nikolic, J., Schneider, T., Hinzmann, T., & Siegwart, R. 2016, Extending Kalibr: Calibrating the extrinsics of multiple IMUs and of individual axes, in 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16-21 May 2016, pp.4304-4311. https://doi.org/10.1109/ICRA.2016.7487628
Sun, W. & Cooperstock, J. R. 2006, An empirical evaluation of factors influencing camera calibration accuracy using three publicly available techniques, Machine Vision and Applications, 17, 51-67. https://doi.org/10.1007/s00138-006-0014-6
Tsai, R. 2003, A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses, IEEE Journal on Robotics and Automation, 3, 323-344. https://doi.org/10.1109/JRA.1987.1087109
Zhang, Z. 2000, A flexible new technique for camera calibration, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22, 1330-1334. https://doi.org/10.1109/34.888718
Zhou, Y., Rupnik, E., Meynard, C., Thom, C., & Pierrot-Deseilligny, M. 2020, Simulation and analysis of photogrammetric UAV image blocks—Influence of camera calibration error, Remote Sensing, 12, 22. https://doi.org/10.3390/rs12010022