Department of Electronic Engineering, Chosun University, Gwangju 61452, Korea
†Corresponding Author: Suk-seung Hwang, E-mail: hwangss@chosun.ac.kr
Citation: Jeon, S.-B. & Hwang, S.-s. 2025, 3D Location Estimation Algorithm Based on the Combined TDOA and FDOA for Fast Moving Object, Journal of Positioning, Navigation, and Timing, 14, 275-280.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 275-280. https://doi.org/10.11003/JPNT.2025.14.3.275
Received on Aug 11, 2025, Revised on Sep 01, 2025, Accepted on Sep 03, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In various aerospace and military applications, precise location estimation techniques are essential to accurately determine the location of objects at specific points in real time. In particular, when estimating the location of a Fast-Moving Object (FMO) with rapid location changes in a short period of time, such as a high-speed aircraft or a train, an algorithm that satisfies both high accuracy and fast processing speed is required. The representative location estimation techniques include Time Difference of Arrival (TDOA) and Frequency Difference of Arrival (FDOA). TDOA provides high accuracy but it does not consider the object’s travel distance during the processing time, which causes serious location errors in the FMO environment. Although FDOA efficiently estimates both location and velocity, it has the disadvantage of being extremely sensitive to the initial location estimate. In this paper, we propose a combined location estimation algorithm with TDOA and FDOA in threedimensional space that efficiently estimates the location of FMOs and compensates the above limitations of both techniques. The proposed algorithm first estimates the initial location of a FMO employing TDOA and then calculates its velocity employing FDOA to predict the FMO’s trajectory. The location estimation performance of the proposed algorithm is evaluated through computer simulations under various scenarios, including different sensors, FMO placement, speed, etc.
localization, TDOA, FDOA, fast-moving object
항공우주 및 군수 분야에서 고속 이동체(Fast-Moving Object, FMO)의 특정 시점에서의 정확한 위치를 추정하는 기술은 핵심적인 기술로 자리 잡고 있다 (Zhou et al. 2025). 특히, 항공기나 미사일 등 FMO의 경우 짧은 시간 동안에도 위치가 크게 변동되므로, 높은 정확도를 유지하면서 빠른 처리 속도를 보유하는 알고리즘 개발이 필수적이다 (Zou et al. 2018, Wang & Li 2021).
대표적인 위치 추정 기법인 Time Difference of Arrival (TDOA)는 센서들에 도달하는 신호간 도착 시간 차이를 기반으로 신호원의 위치를 추정하는 기법으로 높은 위치 정확도를 제공한다 (Qu et al. 2017, Yang 2024). 하지만, TDOA를 통해 위치를 추정하는 시간 동안 FMO는 이미 상당한 거리를 이동하게 되어, 실시간으로 정확한 위치를 추정하기에는 한계가 있다. 또 다른 대표적인 방법인 Frequency Difference of Arrival (FDOA)는 도플러 주파수 차이를 이용하여 이동 신호원의 위치 및 속도를 동시에 추정할 수 있는 장점이 있다 (Hmam 2017). 그러나, 초기 위치 추정 값에 민감하여 단독으로 사용할 경우 안정적인 성능을 보장하기 어렵다.
이를 극복하기 위해 TDOA와 FDOA를 이용하여 이동체의 위치를 추정하기 위한 다양한 연구들이 진행되고 있으며, Jia et al. (2020)와 Wu et al. (2023)는 TDOA와 FDOA를 이용한 이동체의 위치추정 알고리즘을 제안하였고, Seo et al. (2019)는 TDOA, FDOA, Angel of Arrival (AOA)와 Particle Filter (PF)를 적용하여 정확도를 향상시켰다. 또한, Jo et al. (2023)는 2차원 환경을 고려한 FMO 위치추정 알고리즘을 제안하였다. 그러나, 선행연구 대부분은 2차원 환경이나 저속 이동체에 특화되어 있고, 추가적인 보조 기법에 의존하기 때문에 3차원 환경에서 빠르게 이동하는 FMO의 특정 시점 위치 추정에는 한계가 있다. 본 논문은 이러한 한계를 개선하기 위해, TDOA와 FDOA를 결합한 위치추정 알고리즘을 제안한다. 제안된 알고리즘은 먼저 TDOA를 통해 FMO의 3차원 초기 위치를 추정한 후, FDOA를 통해 계산된 속도 추정치를 해당 위치에 적용하여 FMO의 위치 추정 정확도를 개선한다.
본 논문의 구성은 다음과 같다. 2장에서 TDOA와 FDOA 추정 방법을 본 논문에 적합하게 설명하고, 3장에서 제안된 3차원 FMO 위치추정 알고리즘에 대해 설명한다. 4장에서는 컴퓨터 시뮬레이션을 통해 제안된 알고리즘의 성능을 평가하고, 5장은 결론이다.
본 장에서는 제안된 3차원 TDOA/FDOA 결합 알고리즘의 설명을 위해, 3차원 TDOA와 FDOA의 기본 개념을 소개한다.
결합된 TDOA/FDOA 알고리즘의 3차원 FMO 초기 위치를 추정하기 위해 TDOA를 활용한다. $R_i(\mathbf{x})$는 FMO의 위치 $\mathbf{x} = [x,\, y,\, z]^{T}$와 $i$번째 센서의 위치 $\mathbf{x}_{i} = [\, x_{i},\, y_{i},\, z_{i} \,]^{T}$간의 거리로 Eq. (1)과 같이 정의된다.
$$R_i(\mathbf{x})
=
\sqrt{
(x – x_i)^2
+
(y – y_i)^2
+
(z – z_i)^2
},
\qquad i = 1,2,3,4.$$
FMO의 위치로부터 기준 센서인 첫 번째 센서 까지의 거리 $R_{1}(\mathbf{x})$와 $j$번째 센서까지의 거리 $R_{j}(\mathbf{x})$의 차이인 $R_{j,1}(\mathbf{x})$는 Eq. (2)로 정의할 수 있다.
$$R_{j,1}(\mathbf{x})
=
R_j(\mathbf{x})
–
R_1(\mathbf{x}),
\qquad
j = 2,3,4.$$
4개의 센서로부터 얻은 TDOA 측정값은 Eq. (3)과 같이 벡터 형태로 나타낼 수 있다.
$$\mathbf{r}_t(\mathbf{x})
=
\bigl[\, R_{2,1},\; R_{3,1},\; R_{4,1} \,\bigr]^{\!T}$$
평균이 0이고 가우시안 분포를 갖는 잡음 $(\mathbf{n}_t)$을 고려하여, TDOA 측정 오차가 포함된 TDOA 관측값 $(\mathbf{\rho}_t)$은 Eq. (4)로 정의할 수 있다.
$$\boldsymbol{\rho}_t = \mathbf{r}_t(\mathbf{x}) + \mathbf{n}_t$$
계산된 $\mathbf{r}_t(\mathbf{x})$와 $\boldsymbol{\rho}_t$는 FMO의 초기 위치를 추정하기 위해 Iterative Least Squares (ILS) 알고리즘 (O’Donoughue 2019)의 입력 값으로 사용된다. ILS는 반복적으로 추정위치를 개선하는 방법이며, $k$번 반복을 통해 얻은 추정된 위치는 Eq. (5)와 같다.
$$\hat{\mathbf{x}}_{k}
=
\hat{\mathbf{x}}_{k-1}
+
\Delta \mathbf{x}_{k}$$
여기서 $\hat{\mathbf{x}}_{k-1}$은 $k-1$번째 추정된 위치를 의미하며, $\Delta \mathbf{x}_{k}$는 $k$번째 위치 보정 값으로 Eq. (6)과 같다.
$$\Delta \mathbf{x}_{k}
=
\Big[
\,\mathbf{J}(\mathbf{x}_{k})
\,\mathbf{C}_{t}^{-1}
\,\mathbf{J}^{T}(\mathbf{x}_{k})
\Big]^{-1}
\mathbf{J}(\mathbf{x}_{k})
\,\mathbf{C}_{t}^{-1} \,(\mathbf{x}_{k})
\mathbf{T}(\mathbf{x}_{k})$$
여기서 $\mathbf{J}(\mathbf{x}_{k})$는 $k$번째 반복에서 추정된 위치 $\mathbf{x}_{k}$에 대한 자코비안 행렬이며, $\mathbf{C}_{t}$는 $\boldsymbol{\rho}_t$의 오차 공분산 행렬이다 (O’Donoughue 2019). $\mathbf{T}(\mathbf{x}_{k})$는 관측된 TDOA 측정값 ($\boldsymbol{\rho}_t$)과 $k$번째 반복에서 예측된 TDOA 측정값 ($\mathbf{r}_{t}(\mathbf{x}_{k})$)간의 차이이다. 이와 같은 과정을 반복하여 FMO의 초기 위치 $\hat{\mathbf{x}}_{k}$를 결정한다.
결합된 TDOA/FDOA 알고리즘의 3차원 FMO 속도(이동방향 포함)를 추정하기 위해 FDOA를 활용한다. FMO의 속도 $\mathbf{v} = [\, v_x,\; v_y,\; v_z \,]^{T}$, $i$번째 센서의 속도 $\mathbf{v} = [\, v_{xi},\; v_{yi},\; v_{zi} \,]^{T}$, $R_i(\mathbf{x})$를 이용하여 거리 변화율 $\dot{R}_i(\mathbf{x}, \mathbf{v})$를 구할 수 있으며, Eq. (7)과 같이 나타낼 수 있다.
$$\dot{R}_{i}(\mathbf{x}, \mathbf{v})
=
\frac{
(v_{x_i}-v_x)(x-x_i)
+
(v_{y_i}-v_y)(y-y_i)
+
(v_{z_i}-v_z)(z-z_i)
}{R_i}$$
기준 센서인 첫 번째 센서의 거리 변화율 $\dot{R}_1(\mathbf{x}, \mathbf{v})$와 $j$번째 센서의 거리 변화율 $\dot{R}_j(\mathbf{x}, \mathbf{v})$의 차이는 Eq. (8)과 같이 정의할 수 있다.
$$\dot{R}_{j,1}(\mathbf{x},\mathbf{v})
=
\dot{R}_{j}(\mathbf{x},\mathbf{v})
–
\dot{R}_{1}(\mathbf{x},\mathbf{v})$$
4개의 센서로부터 얻은 FDOA 측정값은 Eq. (9)와 같은 벡터 형태로 나타낼 수 있다.
$$\mathbf{r}_f(\mathbf{v})
=
\begin{bmatrix}
\dot{R}_{2,1},\;
\dot{R}_{3,1},\;
\dot{R}_{4,1}
\end{bmatrix}^{T}$$
평균이 0이고 가우시안 분포를 따르는 잡음 ($\mathbf{n}_{f}$)을 고려하여, FDOA 측정 오차가 포함된 FDOA 관측값 ($\dot{\boldsymbol{\rho}}_{f}$)은 Eq. (10)으로 정의할 수 있다.
$$\dot{\boldsymbol{\rho}}_{f}
=
\mathbf{r}_{f}(\mathbf{v})
+
\mathbf{n}_{f}$$
계산된 $\mathbf{r}_{f}(\mathbf{v})$와 $\dot{\boldsymbol{\rho}}_{f}$는 ILS 알고리즘의 입력 값으로 사용되며, $k$번째 반복에서 얻은 속도 추정치는 Eq. (11)과 같다.
$$\hat{\mathbf{v}}_{k}
=
\hat{\mathbf{v}}_{k-1}
+
\Delta \mathbf{v}_{k}$$
여기서 $\hat{\mathbf{v}}_{k-1}$은 $k-1$번째 추정된 속도를 의미하며, $\Delta \mathbf{v}_{k}$는 $k$번째 속도 보정 값으로 Eq. (12)와 같다.
$$\Delta \mathbf{v}_{k}
=
\Big[
\mathbf{J}(\mathbf{v}_{k})\,
\mathbf{C}_{f}^{-1}\,
\mathbf{J}^{T}(\mathbf{v}_{k})
\Big]^{-1}
\mathbf{J}(\mathbf{v}_{k})\,
\mathbf{C}_{f}^{-1}\, (\mathbf{v}_{k}) \,
\mathbf{F}(\mathbf{v}_{k})$$
여기서 $\mathbf{J}(\mathbf{v}_{k})$는 $k$번째 반복에서 추정속도 값 $\mathbf{v}_{k}$에 대한 자코비안 행렬이며, $\mathbf{C}_{f}$는 $\dot{\boldsymbol{\rho}}_{f}$의 오차 공분산 행렬이다 (O’Donoughue 2019). $\mathbf{F}(\boldsymbol{v}_{k})$는 관측된 FDOA 측정값 ($\dot{\boldsymbol{\rho}}_{f}$)과 $k$번째 반복에서 예측한 FDOA 측정값 ($\mathbf{r}_{f}(\mathbf{v}_{k})$)간의 차이이다. 이와 같은 과정을 반복하여 속도 $\hat{\mathbf{v}}_{k}$를 추정한다.
이번 장은 TDOA와 FDOA를 결합한 3차원 FMO 위치추정 알고리즘에 대해 설명한다. 고속으로 이동하는 FMO의 경우, TDOA와 FDOA 프로세싱 시간과 같이 매우 짧은 시간에도 상당한 위치 변화가 생겨 심각한 위치추정 오차가 발생할 수 있다. 이러한 문제점을 개선하기 위해, 본 논문은 두 위치추정 기술의 장점을 활용한 결합된 3차원 위치추정 알고리즘을 제안한다. TDOA를 활용하여 FMO의 초기 위치를 추정하고, FDOA를 활용하여 FMO의 속도와 이동방향을 계산하여 TDOA와 FDOA의 프로세싱 시간 동안 이동한 위치를 예측한다.
TDOA 프로세싱 시간($t_{T}$) 동안 FMO가 이동한 거리를 고려한 위치 예측 값은 Eq. (13)과 같다.
$$\Delta \mathbf{P}
=
\hat{\mathbf{v}}_{k} \times t_{T}$$
FDOA 프로세싱 시간($t_{F}$) 동안 FMO가 이동한 위치 예측 값은 Eq. (14)와 같다.
$$\Delta \mathbf{E}_{n}
=
\hat{\mathbf{v}}_{k} \times t_{F}$$
최종적으로 FMO의 예상 위치는 Eq. (15)와 같다.
$$\begin{align}
\hat{\mathbf{E}}_{n}
&=
\hat{\mathbf{E}}_{\,n-1}
+
\Delta \hat{\mathbf{E}}_{n}
\quad (n \ge 1) \notag \\[6pt]
\hat{\mathbf{E}}_{0}
&=
\hat{\mathbf{x}}_{k}
+
\Delta \mathbf{P}
\end{align}$$
설정된 임의의 시간 ($n=N$)이후, 추가적인 위치 추정이 필요한 경우, Eq. (5)를 이용하여 다시 초기 위치를 추정하고 Eqs. (11-15)를 반복하여 FMO의 위치를 추정한다. Fig. 1은 3차원 환경에서 FMO의 위치를 정밀하게 추정하기 위해 제안된 위치추정 알고리즘의 순서도를 나타낸다. 제안된 알고리즘은 TDOA를 통해 초기 위치를 추정함으로써 FDOA가 갖는 초기 민감성을 상쇄시킨다. 또한, FDOA를 통해 FMO의 속도를 추정하여, 이를 최종 위치 결정에 반영하여 TDOA 및 FDOA 프로세싱 시간으로 인해 발생하는 위치 오차를 보정하여 최종 위치를 결정한다.
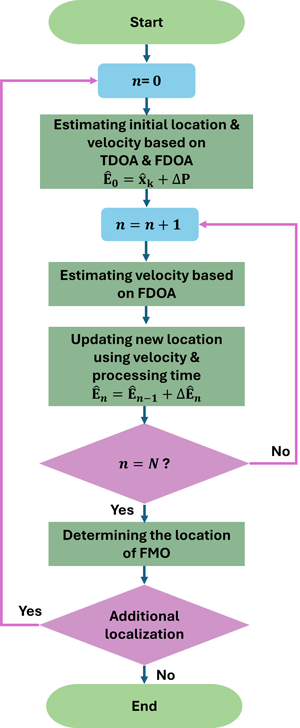
Fig. 1. The proposed FMO location estimation algorithm.
본 장은 FMO를 위한 TDOA와 FDOA가 결합된 3차원 위치추정 알고리즘의 성능평가를 위해 컴퓨터 시뮬레이션 결과를 제시한다. 시뮬레이션은 두 가지 시나리오를 고려하였으며, 알고리즘 평가를 위해 설정된 주요 파라미터들은 Tables 1과 2에 정리되어 있다. 시간 오차와 주파수 오차 (CaJacob et al. 2016, Kim et al. 2022)는 510 ns와 5 Hz 이하로 설정하였고, TDOA 및 FDOA 프로세싱 시간은 MATLAB의 Tic-Toc 함수를 사용하여 측정한 결과, TDOA 프로세싱 시간 0.1초와 FDOA 프로세싱 시간 0.04초로 설정하였다. 또한, 센서들은 서로 다른 궤도 및 고도(2,000 km 이하)로 운용되고 있는 위성 (Deng et al. 2023)들에 탑재되어 있고, FMO는 일정한 속도와 방향으로 이동한다고 가정한다.
Table 1. Parameters for the first scenario.
| Location (km) | Velocity (km/s) | |
|---|---|---|
| Satellite 1 | (800, 2000, 1500) | (4, 6, 5) |
| Satellite 2 | (-1500, -700, 1750) | (3, 7, 4) |
| Satellite 3 | (1800, 600, 1950) | (2, 5, 2) |
| Satellite 4 | (-550, 1250, 1600) | (2, 6, 3) |
| FMO | (200, 50, 8) | (0.25, 0.156, 0.264) |
| Center frequency | 400 MHz | |
| Timing error | 100 ns | |
| Frequency error | 4 Hz | |
| TDOA processing time | 0.1 sec | |
| FDOA processing time | 0.04 sec | |
Table 2. Parameters for the second scenario.
| Location (km) | Velocity (km/s) | |
|---|---|---|
| Satellite 1 | (-1590, 1390, 1900) | (3, 2, 2) |
| Satellite 2 | (4610, 1450, 1850) | (4, 1, 3) |
| Satellite 3 | (900, 800, 2000) | (2, 3, 4) |
| Satellite 4 | (1000, 1250, 1700) | (5, 1, 1.5) |
| FMO | (1100, 1050, 11) | (0.113, -0.09, 0.2) |
| Center frequency | 500 MHz | |
| Timing error | 50 ns | |
| Frequency error | 5 Hz | |
| TDOA processing time | 0.1 sec | |
| FDOA processing time | 0.04 sec | |
Figs. 2와 3은 각 시나리오에서의 센서들과 FMO의 위치와 이동방향을 보여준다. Fig. 4는 첫 번째 시나리오에서 실제 FMO의 위치와 TDOA를 통해 추정된 FMO 위치를 나타낸다. 각 위치에서의 화살표는 FMO의 이동방향을 나타내며, TDOA 프로세싱 시간동안 FMO는 빠르게 특정 방향으로 이동하여 실시간 위치를 특정하기 어려워진다. 이와 같은 이유로, Fig. 4는 TDOA 프로세싱 시간 동안 FMO가 위치할 수 있는 범위를 추정 위치를 중심으로 3차원 구의 형태로 표현하였다. Fig. 5는 총 0.5초(TDOA 1회, FDOA 10회)동안 FMO의 위치를 추정한 결과를 나타낸다.
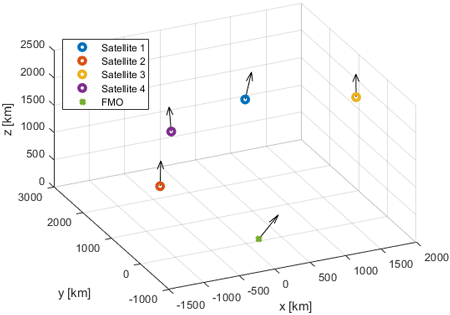
Fig. 2. Locations and moving directions of sensors and FMO for the first scenario.
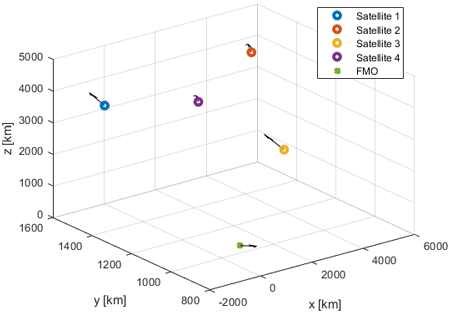
Fig. 3. Locations and moving directions of sensors and FMO for the second scenario.
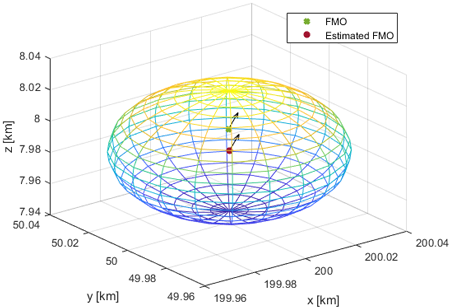
Fig. 4. The estimated FMO location and the expected range for the first scenario.
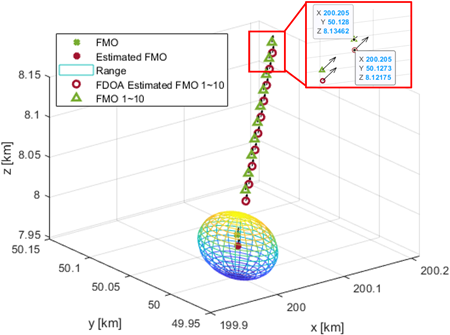
Fig. 5. The estimated result of FMO location for 0.5 second for the first scenario.
Fig. 6은 두 번째 시나리오에서 실제 FMO의 위치와 TDOA를 통해 추정된 FMO 위치를 나타내며, 각 위치에서의 화살표는 FMO의 이동방향을 나타낸다. Fig. 4와 마찬가지로, TDOA 프로세싱 시간동안 FMO의 위치를 특정할 수 없으므로, TDOA 프로세싱 시간 동안 FMO가 위치할 수 있는 범위를 구의 형태로 표현하였다. Fig. 7은 1초 동안(TDOA 2회, FDOA 20회) 2 사이클을 수행한 결과이다. 한 사이클 종료 후, TDOA를 다시 실행하여 두 번째 사이클의 초기 위치를 추정하고, 그 결과를 기반으로 FDOA를 실행하여 FMO의 최종 위치를 추정하였다. 두 시나리오에 대한 FMO의 최종 위치추정 결과를 비교한 결과, 두 번째 시나리오에서 주파수 오차는 증가하였지만, 중심 주파수가 증가하였고 시간 오차가 감소되어 추정 오차가 줄어든 결과를 도출하였다.
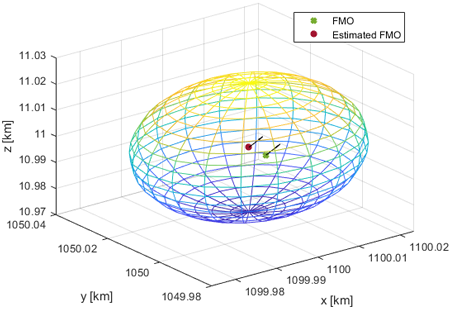
Fig. 6. The estimated FMO location and the expected range for the second scenario.
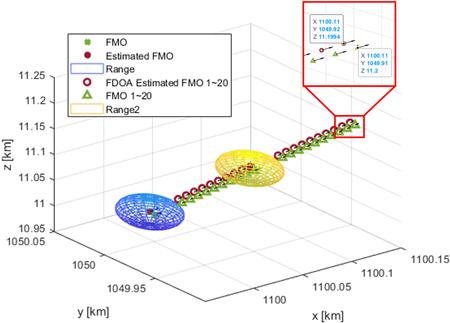
Fig. 7. The estimated result of FMO location for 1.0 second for the second scenario
두 시나리오에 대해 CaJacob et al. (2016)와 Kim et al. (2022)을 참고하여 0~500 ns의 가변 시간 오차, 0~5 Hz의 가변 주파수 오차를 고려하였으며, 위치추정 성능평가를 위해 Eq. (16)과 같이 정의되는 Root Mean Square Error (RMSE)를 활용하였다.
$$RMSE
=
\sqrt{
E\left[
(x-\hat{x})^{2}
+
(y-\hat{y})^{2}
+
(z-\hat{z})^{2}
\right]
}$$
여기서 ($x,\, y,\, x$)는 실제 FMO의 위치이며, ($\hat{x},\, \hat{y},\, \hat{z}$)는 추정된 FMO의 위치이고, RMSE는 100번의 몬테카를로 시뮬레이션을 통해 계산되었다. Figs. 8과 9는 각 시나리오에 대한 시간 및 주파수 오차별 위치추정 RMSE 그래프를 나타낸다. 단일 TDOA는 시간 오차만 고려하므로, 주파수 오차에 관계없이 시간 오차가 증가할수록 RMSE가 증가한다. 두 시나리오에서 TDOA 실행 후 0.5초가 지난 시점의 위치를 비교하므로, 상당한 추정 오차를 보인다. 단일 FDOA는 주파수 오차만 고려하므로, 시간 오차와 무관하게 주파수 오차가 증가할수록 RMSE가 증가한다. 반면, 제안된 알고리즘은 두 가지 오차를 모두 고려하지만, 일반적인 단일 TDOA나 FDOA 방법에 비해 우수한 FMO 위치추정 성능을 보유함을 두 그림으로부터 확인할 수 있다.
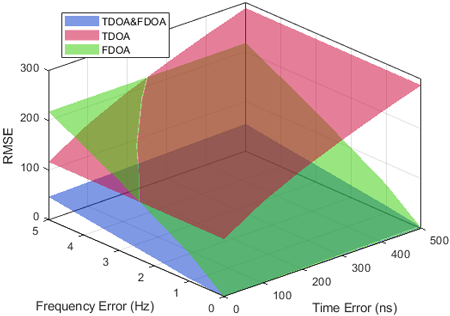
Fig. 8. RMSE results by time errors and frequency errors for the first scenario.
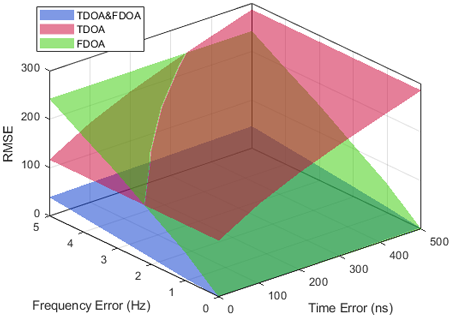
Fig. 9. RMSE results by time errors and frequency errors for the second scenario.
기존의 TDOA 및 FDOA 기반 위치추정 기법은 주로 저속 이동체 환경에 최적화되어 있어, 3차원 환경 FMO의 정밀한 위치추정이 어렵다는 한계가 있다. 본 논문은 FMO의 위치를 효율적으로 추정하기 위해 TDOA와 FDOA를 상호 보완적으로 결합한 3차원 FMO 위치추정 알고리즘을 제안하였다. TDOA와 FDOA 프로세싱 시간, FMO 초기 위치 및 속도를 고려한 제안된 위치추정 알고리즘은 TDOA를 이용하여 FMO의 3차원 초기 위치를 추정하고, 이를 기반으로 FDOA를 통해 이동 방향을 포함한 FMO의 속도를 추정하여, 3차원 환경에서의 FMO 위치를 효율적으로 계산한다. 다양한 환경 변수를 고려한 컴퓨터 시뮬레이션을 통해 3차원 환경에서 제안된 알고리즘의 FMO 위치추정 성능을 확인하였다. 또한, 다양한 시간 오차 및 주파수 오차를 고려한 경우에도 기존의 단일 TDOA와 FDOA 대비 우수한 위치 추정 성능을 보유하여, 항공 및 국방분야를 포함한 FMO의 정확한 위치가 요구되는 다양한 분야에서 유용하게 활용될 수 있을 것으로 판단된다.
이 논문은 2024년도 조선대학교 연구비의 지원을 받아 연구되었음.
Conceptualization, S. B. Jeon. and S. Hwang.; methodology, S. B. Jeon. and S. Hwang.; software, S. B. Jeon.; validation, S. B. Jeon.; formal analysis, S. B. Jeon.; investigation, S. B. Jeon. and S. Hwang.; writing—original draft preparation, S. B. Jeon.; writing review and editing, S. Hwang.; supervision; S. Hwang.
The authors declare no conflict of interest.
CaJacob, D., McCarthy, N., O’Shea, T., & McGwier, R. 2016, Geolocation of RF emitters with a formation-flying cluster of three microsatellites, Proceedings of the 30th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 6–11 August 2016.
Deng, X., Chang, L., Zeng, S., Cai, L., & Pan, J. 2023, Distance-based back-pressure routing for loadbalancing LEO satellite networks, IEEE Transactions on Vehicular Technology, 72, 1240–1253.
https://doi.org/10.1109/TVT.2022.3206616
Hmam, H. 2017, Optimal sensor velocity configuration for TDOA-FDOA geolocation, IEEE Transactions on Signal Processing, 65, 628–637.
https://doi.org/10.1109/TSP.2016.2621724
Jia, T., Ho, K. C., Wang, H., & Shen, X. 2020, Localization of a moving object with sensors in motion by time delays and Doppler shifts, IEEE Transactions on Signal Processing, 68, 5824–5841.
https://doi.org/10.1109/TSP.2020.3023972
Jo, T. H., Park, J.-H., & Hwang, S. 2023, Combined Algorithm with TDOA/FDOA for Estimating Location of High-speed Moving Object, Journal of Korean Institute of Intelligent Systems, 33, 563–569.
https://doi.org/10.5391/JKIIS.2023.33.6.563
Kim, H., Lee, G. H., Cho, D., Park, J., Choi, D., et al. 2022, Mission and System Design of LEO Satellite-based Signal Acquisition, Proceedings of the Korean Society for Aeronautical and Space Sciences, Jeju, Korea, 16 November 2022, pp. 1551–1553.
O’Donoughue, N. 2019, Emitter detection and geolocation for electronic warfare (Boston: Artech House Inc.)
Qu, X., Xie, L., & Tan, W. 2017, Iterative constrained weighted least squares source localization using TDOA and FDOA measurements, IEEE Transactions on Signal Processing, 65, 3990–4003.
https://doi.org/10.1109/TSP.2017.2703667
Seo, H., Kim, H., Kang, J., Jeong, I., Ahn, W., et al. 2019, 3D moving target tracking with measurement fusion of TDoA/FDoA/AoA, ICT Express, 5, 115–119.
https://doi.org/10.1016/j.icte.2018.07.003
Wang, H., & Li, L. 2021, An effective localization algorithm for moving sources, Eurasip Journal on Advances in Signal Processing, 32.
https://doi.org/10.1186/s13634-021-00745-3
Wu, H., Wu, Z.-H., Shi, Z.-S., & Sun, S.-Y. 2023, Research on multi-moving target location algorithm based on improved TDOA/FDOA, Measurement and Control, 56, 938–952.
https://doi.org/10.1177/00202940221136246
Yang, X. 2024, Enhanced Moving Source Localization with Time and Frequency Difference of Arrival: Motion-Assisted Method for Sub-Dimensional Sensor Networks, Applied Sciences, 14, 3909.
https://doi.org/10.3390/app14093909
Zhou, X., Jia, W., He, R., & Sun, W. 2025, High-Precision Localization Tracking and Motion State Estimation of Ground-Based Moving Target Utilizing Unmanned Aerial Vehicle High-Altitude Reconnaissance, Remote Sensing, 17, 735. http://doi.org/10.3390/rs17050735
Zou, Y., Liu, H., & Wan, Q. 2018, An iterative method for moving target localization using TDOA and FDOA measurements, IEEE Access, 6, 2746–2754. http://doi.org/10.1109/ACCESS.2017.2785182