1Department of Aeronautical and Astronautical Engineering, Korea Aerospace University, Gyeonggi-do 10540, South Korea
2Satellite Application Research Team at Korea Aerospace Research Institute (KARI), Daejeon 34133, South Korea
Citation: Yoon, S., Kim, Y., Kim, H., & Kim, J. 2025, Prediction Method of Zenith Wet Tropospheric Delay with LSTM Model, Journal of Positioning, Navigation, and Timing, 14, 281-289.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 281-289. https://doi.org/10.11003/JPNT.2025.14.3.281
Received on Aug 12, 2025, Revised on Aug 24, 2025, Accepted on Aug 27, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Global navigation satellite system (GNSS) signal delay caused by the troposphere is a significant source of error for precision positioning. To mitigate this tropospheric delay effect, a precise point positioning (PPP) method estimates the tropospheric delay with carrier phase ambiguities. With accurately predicted tropospheric delay, this delay effect can be effectively minimized or the tropospheric delay estimation process can be improved. An artificial intelligence technique, Long Short-Term Memory (LSTM), was developed to predict the wet tropospheric delay using meteorological observations such as temperature, pressure, and relative humidity at GNSS monitoring stations. Five years of meteorological observation data from four GNSS measuring stations in the Korea were used to train the LSTM network model, which predicts one year of wet tropospheric delays at those stations. The predicted wet delays are compared with the wet delays estimated by the PPP method, and the forecast accuracy and geographical error differences are discussed.
GNSS, tropospheric delay, zenith wet delay, LSTM, artificial intelligence, time series forecasting
위성항법시스템 (Global Navigation Satellite System, GNSS) 신호는 대기를 통과하는 과정에서 전리층 및 대류층에 의한 신호지연이 발생하며, 이로 인해 적절한 보정 없이 GNSS를 활용할 경우 측위 정확도가 크게 저하될 수 있다. 특히 대류층 지연은 신호가 지표면에서 가까운 대류층을 통과할 때 발생하는 지역적 오차로, 대류층에 의한 신호지연은 수 미터 이상의 위치 오차를 유발하는 주요 요인 중 하나이다. 이 때문에 GNSS 기반 고정밀 위치결정에서는 대류층 지연의 정밀한 추정과 예측이 필수적이다 (Hofmann-Wellenhof et al. 2001).
대류층 천정 지연 (Zenith Total Delay, ZTD)은 건조지연 (Zenith Hydrostatic Delay, ZHD) 및 습윤지연 (Zenith Wet Delay, ZWD)으로 구성된다. 건조지연은 대기압이나 온도처럼 변화가 비교적 적고 안정적인 대기 변수에 의해 결정되기 때문에, 다양한 경험적 대기 모델을 활용하여 높은 정확도로 추정 가능하다. 대표적으로 University of New Brunswick 3 modified (UNB3m) 모델이나 Saastamoinen 모델은 관측된 대기압, 기온, 수신기 위치 정보 등을 입력하여 ZHD를 산출하며, 이 값은 계절이나 위치에 따른 변화에도 비교적 정확하게 동작한다. 이에 비해 ZWD는 대기의 순간적인 변화와 국지적인 기상 조건에 크게 좌우되므로, 경험적 모델이나 단순한 보정 기법만으로는 충분한 정확도를 얻기 어렵다 (Bevis et al. 1992).
그렇기 때문에 ZWD 예측에 관한 연구가 최근 머신러닝과 딥러닝 기법을 중심으로 활발히 이루어지고 있다. Katsougiannopoulos & Pikridas (2009)는 GPS 상시관측소의 위치 정보와 시간 데이터를 입력 데이터로 사용하여 Multi-Layer Perceptron (MLP) 모델로 ZTD 예측을 수행하였다. Selbesoglu (2020)는 Artificial Neural Network (ANN)을 이용하여 최대 6시간 후의 ZWD를 예측하였다. Bi et al. (2024)는 1차원 합성곱 신경망 (Convolution Neural Network, CNN)을 활용해 2018년 중국 기상관측소의 ZWD를 예측하였고, Global Pressure and Temperature (GPT) 3 등의 기존 모델 대비 Root Mean Squared Error (RMSE)가 감소함을 보고하였다. Chen & Gao (2024)는 Long Short-Term Memory (LSTM) 및 Feed Forward Neural Network (FFNN) 모델을 이용해 실시간 ZWD를 예측하였다. Wu et al. (2024)는 CNN-LSTM 모델을 통해 2022년 남미에서 ZWD를 예측하였고, Li et al. (2022)과 Li et al. (2023)은 LSTM, Back Propagation Neural Network (BPNN), Random Forest (RF) 등 다양한 머신러닝 기법을 적용해 각각 남극과 중국에서의 ZWD 예측 정확도를 개선하였다. 국내에서도 Lim & Bae (2021)은 기상 데이터를 입력으로 LSTM과 Multi-Layer Perceptron (MLP) 기반 ZWD 추정 모델을 제안하여 2015년 10월-11월 수원의 ZWD를 예측하였다.
본 연구에서는 시계열 데이터 예측에 강점을 가진 LSTM 모델을 적용하여 (Hochreiter & Schmidhuber 1997), 2017년부터 2022년까지 6년에 걸친 국내 GNSS 상시관측소의 관측데이터와 기상데이터를 활용해 2022년 한 해 동안의 ZWD 예측 성능을 분석하였다. European Space Agency (ESA)에서 만든 소프트웨어인 gLAB의 PPP 기능을 통해 ZTD를 추정하였으며, ZHD를 산정하기 위해서 캐나다의 University of New Brunswick (UNB)에서 개발한 UNB3 모델을 사용하였다. 예측 모델의 입력 변수로는 각 관측소에서 획득한 기압, 기온, 상대습도 등 주요 기상 자료와 시간에 대한 파라미터를 사용하였다. 본 연구의 가장 큰 특징은, 단기 데이터가 아니라 다양한 계절과 기상 조건, 그리고 실제 환경 변동성이 반영된 6년간의 장기간 실측 데이터를 바탕으로, LSTM 모델이 ZWD 예측에 있어 얼마나 안정적이고 신뢰성 있게 동작하는지를 체계적으로 평가했다는 데 있다.
본 논문의 2장에서는 ZWD 예측에 사용된 기법의 이론에 대해 설명하고, 3장에서는 예측에 사용한 데이터와 전처리 결과에 대해 설명하였다. 4장에서는 LSTM 모델의 구조와 최적화 결과를 제시하고 5장에서는 ZWD 예측 성능분석을 수행하였다.
LSTM 모델은 Recurrent Neural Network (RNN)에서 발생하는 장기 종속성 문제를 해결하기 위한 딥러닝 기법이다 (Hochreiter & Schmidhuber 1997). RNN은 장기 데이터를 학습할 때 역전파 과정에서 기울기가 소실되어 가중치 갱신이 제대로 이루어지지 않는 문제를 가진다. 이것을 해결하기 위해 LSTM 네트워크는 입력 게이트, 망각 게이트 및 출력 게이트를 활용하여 RNN의 은닉 상태에서 셀 상태를 제어한다. LSTM 구조는 각 게이트가 현재 입력과 이전 네트워크 출력을 결합하여 게이트 출력을 계산하며, 이는 Eq. (1)과 같이 표현된다 (Cui et al. 2018).
$$f_t = \sigma\left( W_x x_t + W_h h_{t-1} + b_f \right)$$
여기서 $W_x$와 $W_h$는 각각 현재 입력 $x_t$와 이전 출력 $h_{t-1}$에 곱해지는 가중치 행렬을 의미하며, $b$는 각 게이트별 편향치에 해당한다. 망각 게이트 (forget gate)는 시그모이드 함수 값을 통해 이전 셀 상태 $c_{t-1}$에서 어떤 정보를 보존할지 결정한다.
새로운 셀 상태 $c_t$는 입력 게이트 (input gate)의 출력값과 새로운 후보 셀 상태 $g_t$를 곱하여, 망각 게이트를 거친 이전 셀 상태와 합산함으로써 계산된다. 이 과정은 Eq. (2)와 같이 표현된다.
$$c_t = f_t \ast c_{t-1} + i_t \ast g_t$$
여기서 $i_t$는 입력 게이트의 시그모이드 출력, $g_t$는 입력값과 이전 출력에 대해 하이퍼볼릭 탄젠트 함수를 적용한 결과값이다. $i_t$와 $g_t$의 곱은 셀 상태에 새롭게 추가될 정보의 양을 결정한다.
마지막으로, 출력 게이트 (output gate)는 현재 셀 상태 $c_t$에 하이퍼볼릭 탄젠트 함수를 적용한 결과에 출력 게이트의 시그모이드 값을 곱하여 최종 출력 $h_t$를 생성한다. 이 연산은 Eq. (3)과 같이 나타낼 수 있다.
$$h_t = o_t \ast \tanh(c_t)$$
여기서 $o_t$는 출력 게이트의 활성화 값으로, 현재 입력 $x_t$, 직전 시점의 출력 $h_{t-1}$, 그리고 셀 상태와 결합되어 시그모이드 함수로 연산된다. LSTM 셀이 내부 상태의 정보를 얼마만큼 외부로 전달할지 조절하며, 이는 Eq. (4)와 같이 나타낼 수 있다.
$$o_t = \sigma\left( W_{xo}\, x_t + W_{ho}\, h_{t-1} + b_o \right)$$
여기서 $W_{xo}$와 $W_{ho}$는 각각 출력 게이트에 대한 가중치 행렬이고, $b_0$는 출력 게이트의 편향을 의미한다. LSTM 네트워크는 시계열 데이터의 분석 및 예측 문제에서 탁월한 성능을 보이는 순환 신경망 (RNN)의 대표적 구조이다.
본 연구에서 개발한 LSTM 기반 ZWD 예측 모델은 일일 시간, 계절 정보 및 기상관측값을 반영하여 ZWD를 예측하도록 구성되었다. Table 1은 LSTM 모델의 7개 입력 데이터 및 출력데이터를 정리한 것이다.
Table 1. Data source and simulation parameters.
| Input/Output | Data type | Parameter |
|---|---|---|
| Input | Time | Hour of day – cosine |
| Hour of day – sine | ||
| Day of year – cosine | ||
| Day of year – sine | ||
| Metrological | Pressure (P) | |
| Temperature (T) | ||
| Relative humidity (RH) | ||
| Output | Tropopsheric delay | Zenith wet delay (ZWD) |
시간에 관한 입력 데이터로는 연중 날짜 (day of year, DOY)과 일일중 시간 (hour of day, HOD)을 사용하였는데, 각각 cosine 및 sine 형태의 두 개씩 파라미터로 분리하여 사용하였다. 이는 해나 날짜가 변경되는 시점에서 입력 데이터의 연속성을 보전하기 위한 방법이다. 기상변수로는 대기압 (pressure), 기온 (temperature) 및 상대습도 (relative humidity)를 선정하였는데, 이는 다양한 반복시험 등을 통해 도출한 입력 파라미터 조합이다.
네트워크 구조는 입력층을 시작으로 두 개의 LSTM 계층을 순차적으로 지나도록 하였다. 첫 번째 LSTM 계층에서는 입력된 시계열 데이터의 low-level 단기 패턴을 학습하며, 그 출력을 두 번째 LSTM 계층에서 받아 장기적 의존성과 특징을 모델링한다. 이는 깊이가 얕은 단일 계층 구조보다 표현력과 학습 효율성에서 유리하며, 실제로 Sutskever et al. (2014)의 연구에서도 심층 LSTM 계층 구조가 더 우수한 성능을 보여준 바 있다. 이러한 Stacked LSTM은 상대적으로 더 적은 뉴런과 빠른 학습으로도 복잡한 함수 근사에 효과적인 반면, 계층 수가 과도하면 과적합, 학습 불안정성 및 계산 비용 증가 등의 문제를 초래할 수 있다 (Zaremba et al. 2014). 각 LSTM 계층에는 여러 개의 은닉 노드가 포함되어 있으며, 시계열 데이터의 시간적 연관성을 학습한다. 이후 완전연결 (Fully Connected, FC) 계층을 거쳐, 최종적으로 ZWD를 예측한다. 각 계층의 활성화 함수는 예측 성능을 극대화하기 위해 Rectified Linear Unit (ReLU)를 적용하였으며, 계층 및 노드 수는 최적화 과정을 통해 결정하였다. Fig. 1은 LSTM Cell 내부에서 ZWD 예측 모델의 과정과 데이터 입출력 과정을 보여준다.
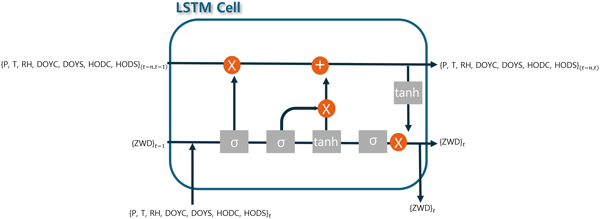
Fig. 1. The architecture and input/output of LSTM.
Bayesian 최적화는 복잡한 하이퍼파라미터 조합에서 목적함수의 최적값을 효율적으로 탐색하는 확률론적 기법으로, 계산 비용이 높은 모델 (LSTM 등)의 하이퍼파라미터 튜닝에 특히 유리하다 (Brochu et al. 2010). 해당 기법은 관측된 목적 함수 값을 바탕으로 함수의 분포를 확률적으로 추정하고, 새로운 데이터가 추가될 때마다 사후분포를 갱신하여 탐색 효율을 높인다. 이 과정에서 이미 충분히 탐색된 영역은 피하고, 불확실성이 높은 영역을 우선적으로 탐색한다. 이러한 특성으로 인해 제한된 계산 자원이나 실험 횟수 내에서 높은 성능을 확보할 수 있다.
Bayesian 최적화의 절차는 초기 하이퍼파라미터 조합을 무작위로 평가한 뒤, Gaussian Process 등의 확률 모델로 사후분포를 추정 및 업데이트하고, 획득 함수 (acquisition function)를 최대화하는 지점을 다음 후보로 선정하는 순서로 진행된다. 획득 함수는 탐색과 활용 (exploration-exploitation)의 균형을 조절해 전역 최적해 탐색을 돕는다. 이로써 무작위 탐색이나 그리드 탐색보다 훨씬 적은 연산으로도 전역 최저점 (global minimum)에 도달할 가능성을 높일 수 있다 (Snoek et al. 2012).
한국천문연구원 (Korea Astronomy and Science Institute, KASI)은 전국에 9개 GNSS 상시관측소를 운영 중이며, 각 상시관측소별 기상관측데이터를 제공하고 있다. 본 연구에서는 Fig. 2와 같이 대전 (DAEJ), 제주 (JEJU), 속초 (SKCH), 밀양 (MLYN) 4개 상시관측소의 기상데이터를 사용하였으며, 전국에 골고루 분포되어 있다.
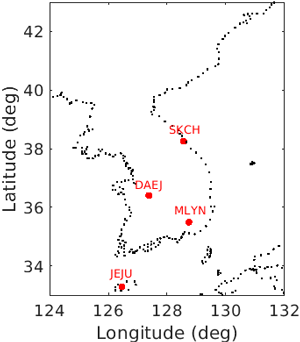
Fig. 2. Location of KASI GNSS monitoring stations used for processing.
각 상시관측소에서는 기상장비를 활용하여 온도, 압력 및 상대습도 등의 기상관측데이터를 수집하고 있다. KASI에서 제공하는 기상데이터는 1분 간격인데, 노이즈에 의한 영향을 완화시키고 ZWD 예측 간격과 맞추기 위하여 이동평균필터를 사용하여 5분 간격의 데이터로 변환하였다.
Fig. 3은 DAEJ 관측소에서 2017년부터 2022년까지 6년간 수집된 기상관측데이터를 나타내고 있다. 기상관측데이터의 노이즈를 줄이기 위하여 이동평균필터를 적용한 결과에 해당하며, 각각의 기상 데이터는 뚜렷한 계절별 변화 경향을 보이고 있다. Table 2에 제시된 2018년도 관측소별 기압, 기온, 상대습도의 통계량에서 볼 수 있듯이 지역적인 편차도 존재하는데, 최남단에 위치하고 도서지역인 JEJU의 경우 다른 관측소에 비해 기상변수의 변화량이 크지 않으며, 해양성기후 성격을 가지는 SKCH는 고기압의 영향으로 타 지역에 비해 습도가 약간 낮다 (KMA 2025a).
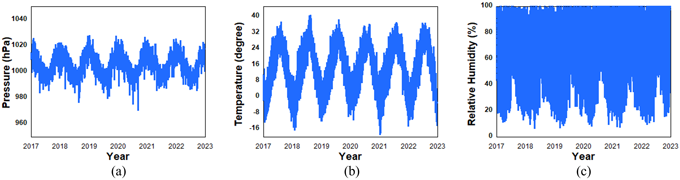
Fig. 3. Meteorological data of DAEJ from 2017 to 2022.
Table 2. Statistics of pressure, temperature, and relative humidity for each KASI ground stations in 2018.
| Station | Pressure (hPa) | Temperature (°) | Relative humidity (%) | |||
|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | |
| DAEJ | 1005.9 | 8.1 | 12.7 | 11.8 | 69.8 | 21.7 |
| JEJU | 969.9 | 6.0 | 12.8 | 8.1 | 70.2 | 18.1 |
| SKCH | 1013.5 | 7.5 | 13.4 | 10.0 | 61.0 | 22.4 |
| MLYN | 1013.4 | 7.6 | 16.8 | 11.4 | 63.0 | 22.7 |
LSTM 기반 ZWD 예측 모델의 학습 및 평가를 위해서는 학습기준값 또는 참값으로 사용할 정밀한 ZWD 값이 필요하다. 각 상시관측소별로 장기간 ZWD 값이 필요한데, 이는 상시관측소에서 수집한 GNSS 데이터를 이용하여 PPP를 수행하면 얻을 수 있다. PPP 과정에서 모호정수 추정을 위해서는 ZTD 추정이 필수적인데, ZTD 추정값에서 모델로 계산한 ZHD를 차감하면 ZWD를 계산할 수 있다. ZHD는 모델만을 사용하더라도 오차가 크지 않기 때문에 ZTD를 정밀하게 추정할 경우 ZWD도 정밀하게 추정하는 것이 가능하다. 한편, DAEJ 관측소는 IGS 기준국이므로 IGS에서 정밀한 ZTD 추정값을 제공한다. 이를 이용하여 본 연구에서 추정한 ZTD값의 정확도를 검증하였다. Fig. 4는 6년간 대전 IGS와 PPP에서 추정된 ZTD의 차이를 나타낸다. 추정 결과, PPP 기반 ZTD와 IGS ZTD 추정 데이터 간의 평균 오차는 -0.004 m, 표준편차는 0.010 m, 최대 오차는 0.200 m로 산출되어, 장기간에 걸쳐 두 데이터가 전반적으로 매우 높은 정합성을 유지함을 확인할 수 있었다. 이러한 결과는 본 연구에서 산출한 PPP 기반 ZTD 참값이 IGS ZTD 추정 데이터와 비교해 장기적으로도 신뢰할 수 있는 수준임을 보여준다.
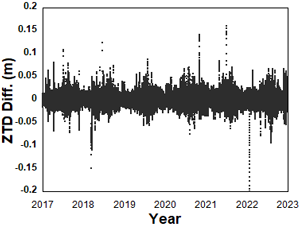
Fig. 4. Difference between IGS ZTD and PPP ZTD in DAEJ station from 2017 to 2022.
Fig. 5는 각각 DAEJ, JEJU, SKCH 및 MLYN 상시관측소에서 6년간 추정한 ZTD 및 ZHD를 나타내고 있다. ZTD는 gLAB 프로그램의 PPP를 사용하여 추정하였으며, ZHD는 UNB3m 모델을 사용하여 추정하였다. ZWD는 ZTD와 ZHD의 차이이다. 모든 관측소의 ZTD를 비교했을 때, 제주 상시관측소에서 ZTD 값이 가장 낮은 것을 확인할 수 있었는데, 이는 지리적 위치에 따른 기압, 기온 및 상대습도의 차이에 기인한 것으로 생각된다.
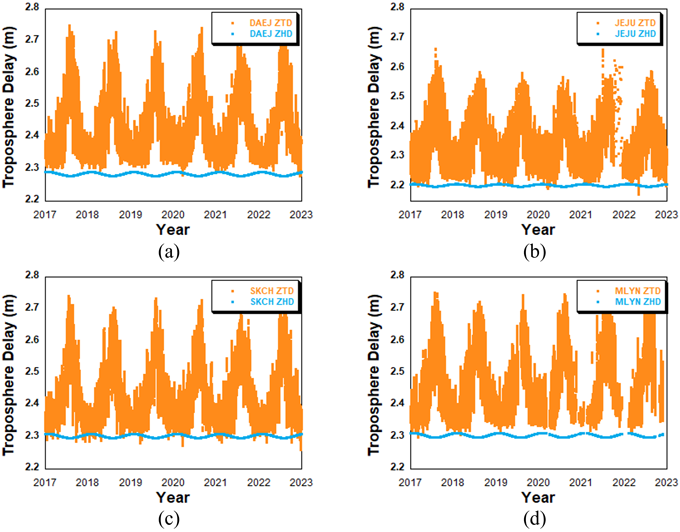
Fig. 5. Estimated KASI stations’ ZTD and ZHD from 2017 to 2022.
Fig. 6은 DAEJ 상시관측소에서 2017년 1월부터 2022년 12월까지 6년간 추정한 ZTD, ZHD 및 ZWD를 나타내고 있다. 기상데이터와 같이 뚜렷한 계절적 변화 경향을 보이고 있지만, 연도별 변화는 크지 않다. 이는 태양활동에 직접적인 영향을 받는 전리층변화와 다른 점이다.
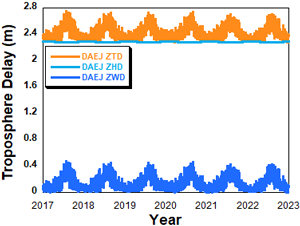
Fig. 6. Estimated and modeled zenith total delays at DAEJ from 2017 to 2022.
LSTM 모델의 예측 성능을 최대화하기 위해 입/출력 데이터를 평균이 0이고 표준편차가 1인 정규분포를 가지도록 표준화를 수행하였으며, 모델의 파라미터를 탐색하기 위하여 Bayesian 최적화 기법을 적용하였다. LSTM 모델의 성능은 학습률 (learning rate), 반복횟수 (epoch), 미니배치 크기 (mini-batch size), 학습률 감소 주기 및 감소율 (learning rate drop period, factor), 은닉층 수와 노드 수, 활성화 함수 등 다양한 하이퍼 파라미터 조합에 따라 크게 달라진다. 하지만 이러한 파라미터의 조합이 매우 많기 때문에, 기존의 무작위 탐색 (random search)이나 그리드 탐색 (grid search) 방식은 계산 효율성과 최적 조합 도출 측면에서 한계가 있다 (Bergstra & Bengio 2012, Snoek et al. 2012). 이에 따라, 본 연구에서는 Bayesian 최적화 기법을 도입하여 적은 계산 횟수로도 효과적으로 최적 조합을 탐색할 수 있도록 하였다.
최적화는 총 2단계로 진행되었다. 먼저 1단계에서는 은닉층 노드 수 제외 주요 하이퍼 파라미터의 초기 탐색 범위를 설정한 후, Bayesian 최적화로 100회의 탐색을 반복 수행하여 적합한 하이퍼 파라미터 조합을 도출하였다. 이어 2단계에서는 1단계 결과를 바탕으로 두 개 LSTM 계층의 은닉 노드 수를 집중적으로 탐색하였으며, 이 역시 100회의 탐색을 통해 최적의 구조를 결정하였다. 각 최적화 단계에서는 별도의 조기 종료 조건을 두지 않고, 사전에 설정한 100회의 탐색 반복을 종료 조건으로 하였다. 이는 예비 실험에서 약 50회 전후로 목적 함수 값이 수렴하는 경향을 확인하였으나, 탐색 안정성을 확보하기 위해 반복 횟수를 100회로 설정하였는데, 실제로 100회 반복 수행 결과, 탐색 후반부에서는 성능 개선 폭이 미미하여 탐색이 수렴하였음을 확인하였다. Fig. 7에는 Bayesian 최적화 과정에서 두 은닉층의 노드 수 조합에 따른 예측오차의 RMS 변화를 도시하였으며, 하단의 빨간색 점이 최적 조합일 때의 최소 RMS를 나타낸다. 각 단계별 최적화 결과 및 최종적으로 선정된 하이퍼 파라미터 조합은 Table 3에 정리하였다. 최적화에는 대전 상시관측소의 전체 기간 관측 데이터를 사용하였다.
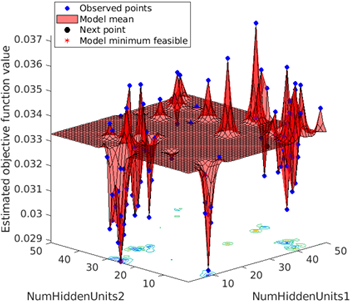
Fig. 7. Searching number of hidden units by Bayesian optimization.
Table 3. Optimized hyperparameters for the LSTM prediction.
| Hyperparameter | Value |
|---|---|
| Optimizer | Adam |
| Epoch | 50 |
| Mini batch size | 1000 |
| Learning rate | 0.005 |
| Learning rate schedule | Constant |
| Num hidden Unit 1 | 5 |
| Num hidden Unit 2 | 25 |
LSTM 모델 학습 시에는 가능한 많은 데이터를 사용하는 것이 유리하므로 2017년 1월부터 2021년 12월까지 5년간의 기상데이터와 ZWD 데이터를 학습에 활용하였고, ZWD 예측 기간은 2022년 1월부터 12월까지 1년으로 설정하였다. ZTD는 1년 주기를 가지므로, 5년간의 데이터는 총 다섯번의 변화 주기를 포함하여 ZTD의 계절별 변화 특성을 반영하기에 적합하다. 입력 데이터 간격은 5분으로 비교적 짧게 설정하였는데, 이는 출력데이터 ZWD 간격을 5분으로 설정하였으므로 입력 데이터 시간간격을 출력 데이터의 시간간격과 일치시켰다. Fig. 8은 SKCH 상시관측소의 ZWD 데이터 중 LSTM 모델 학습에 사용된 ZWD 데이터와 예측에 사용된 ZWD 데이터 구간을 나타낸다.
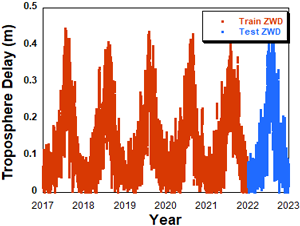
Fig. 8. Train and prediction data period of ZWD at SKCH station from 2017 to 2022.
본 연구에서는 학습데이터를 이용하여 LSTM 네트워크를 구성한 뒤 2022년 1년 동안의 ZWD를 네트워크 갱신없이 예측하였다. 이는 고정된 네트워크로 장기간 예측하는 경우의 예측성능 저하를 살펴보는 것을 목표로 하기 때문이다. 한편, 다음 시점의 ZWD를 예측하기 위하여 과거 1일 입력 데이터를 사용하여 학습하였다.
4개 KASI 상시관측소의 5년간 기상데이터를 이용하여 LSTM 학습을 진행한 뒤, 2022년 1월부터 12월까지 1년간 ZWD 예측결과를 제시하였다. Fig. 9는 MLYN 및 DAEJ 상시관측소에서 2022년 7월 2일과 11월 2일의 ZWD 추정값 (PPP)과 예측 결과 (LSTM)을 비교한 것이다. 해당 날짜의 예측 결과는 PPP 추정 결과와 비슷한 수준을 유지하는 모습을 볼 수 있다. 여름철에는 고온 다습한 환경에서 ZWD의 절대값과 변동성이 모두 증가하기 때문에, ZWD 예측값 범위가 0.2 m 이상으로 그림에는 나타나지 않았지만 ZWD 범위가 0.1 m 근처인 겨울철의 예측보다 오차가 전반적으로 증가하는 경향이 나타났다 (KMA 2025b).
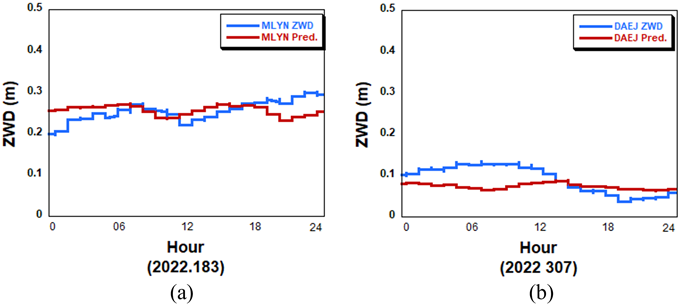
Fig. 9. ZWD prediction of (a) MLYN on July 2 and (b) DAEJ on November 2, 2022.
계절에 따른 예측 성능의 차이를 확인하기 위해 여름 (2022년 7월, DOY 182-212)과 겨울 (2022년 11월, DOY 305-334)을 대표 구간으로 선정하여 4개 KASI 상시관측소의 예측 결과를 비교하였다. Fig. 10은 4개 KASI 상시관측소의 2022년 7월과 11월, 각각 1개월간 4개 KASI 상시관측소의 ZWD 예측 오차를 제시하고 있는데, 계절별 예측 오차 특성 및 실제 예측값의 시계열 변화를 확인할 수 있다. 각 KASI 상시관측소의 7월 예측 RMS 오차는 대전이 0.045 m, 속초와 제주가 각각 0.054 m, 0.055 m, 밀양이 0.041 m에 해당하는 반면, 11월 예측 RMS 오차는 대전과 속초가 각각 0.024 m, 0.025 m, 제주와 밀양이 0.029 m로 ZWD의 변화가 큰 여름철보다 ZWD의 변화가 작은 겨울철의 예측 성능이 더 좋다는 것을 확인하였다.
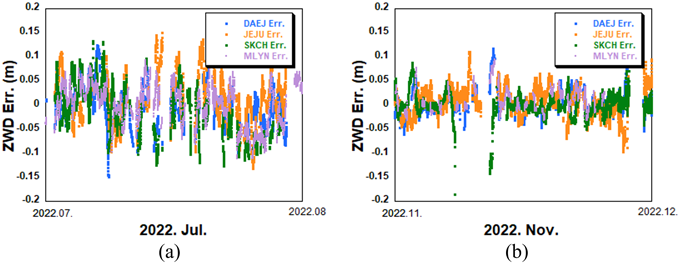
Fig. 10. ZWD prediction errors of four KASI stations in (a) July 2022 and (b) November 2022.
Fig. 11은 LSTM 모델을 활용하여 각각 대전, 제주, 속초, 밀양 상시관측소의 2022년 ZWD를 예측한 결과를 나타내고 있다. 파란색은 각 상시관측소의 ZWD 추정값이며, 빨간색은 본 연구에서 제안한 LSTM 모델로 예측한 결과이다. Fig. 12에서는 각 상시관측소의 예측 오차를 비교하고 있다. 모든 ZWD 시계열은 전반적으로 여름철에 큰 값을 나타낸다. DAEJ 상시관측소의 경우, 2022년 7월에는 평균 0.282 m, 표준편차 0.059 m로 관측되었다. 그러나 겨울철인 2022년 11월에는 평균 0.086 m, 표준편차 0.033 m로, 여름철에 비해 값이 작고 변동성이 낮은 양상을 보였다. 이러한 경향은 여름철에 고온다습한 우리나라 기후 특성상 ZWD가 대류권 내 수증기량에 민감하게 반응한다는 물리 특성과 일치하며, 이러한 환경에서는 ZWD의 절대값과 변동성이 모두 증가함을 나타낸다. 예측된 결과는 이러한 계절 변동성과 급격한 변화 패턴을 0.030 m 이내의 오차 수준으로 반영하고 있음을 알 수 있다. KASI 밀양 상시관측소의 경우, 데이터의 불연속성이 일부 존재하는데, 이는 PPP에 사용되는 KASI 관측 데이터의 누락 또는 입력 변수로 사용되는 기상 데이터의 누락과 관련이 있다.
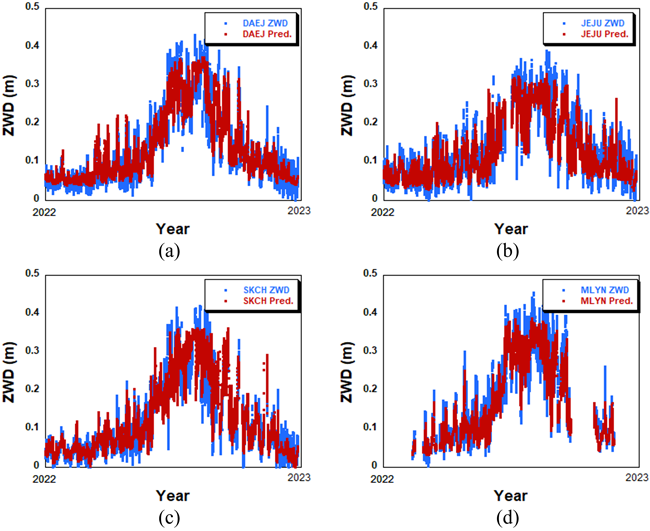
Fig. 11. Each KASI stations’ prediction results in 2022.
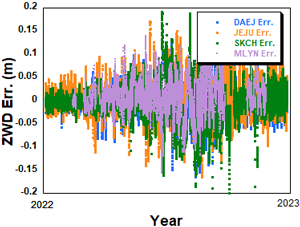
Fig. 12. Each KASI stations’ prediction errors in 2022.
Table 4는 2022년 1년간 KASI 대전 (DAEJ), 제주 (JEJU), 속초 (SKCH), 밀양 (MLYN) 4개 상시관측소의 ZWD 예측 결과에 대한 오차 통계를 비교한 것이다. 각 상시관측소에 대해 예측값과 실제 ZWD 간의 오차 평균, 오차에 대한 표준편차, 평균 제곱근 오차 (RMSE), 최대 절대 오차 (Maximum Absolute Error, MAXAE), 마지막으로 평균 절대 오차 (Mean Absolute Error, MAE)를 산출하였다. Fig. 13은 KASI 상시관측소별 ZWD 예측 오차를 비교하여 보여준다. 전체적으로 RMS 오차는 약 0.030 m, MAE는 약 0.020 m 수준으로 유지되었다. 이는 네 개 KASI 상시관측소에서 관측된 ZWD 범위 (0.05 m – 0.5 m)에 비해 약 5% 내외의 오차 수준에 해당한다. 모든 상시관측소에 대하여 평균 오차는 0.010 m 이하로 유지되었으며, 이러한 이유로 대부분 RMS 오차 결과는 오차의 표준편차 결과와 유사하다. 예측 오차는 대전과 속초 상시관측소에서 RMS 오차가 각각 0.029 m, 0.030 m, MAE가 0.020 m로 가장 좋은 예측 성능을 보였다. MAXAE는 대전이 0.164 m, 속초가 0.215 m로 대전의 예측 성능이 더 좋았다. 이는 Table 2에서 볼 수 있듯 내륙 중부에 위치한 대전의 상대습도가 평균적으로 더 높지만, 해양성 기후와 고기압의 영향을 받는 속초에 비래 전형적인 대륙 기후 특성을 보여 예측이 상대적으로 용이했기 때문이라고 판단하였다. Table 2에서 대전 (DAEJ)의 평균 상대습도는 69.8%로 속초 (SKCH)의 61.0%보다 높으나 변동성은 속초보다 작게 나타나는데, 이는 분지 지형을 기반으로 한 대륙성 기후 특성상 대전의 습도 변화가 계절적, 지역적 변동성에 의해 크게 요동치지 않고, 예측 안정성을 확보하는 데 유리했음을 시사한다. 반면 속초는 해양성 기후와 foehn 현상, 양간지풍 등 지역적 특수 기후 현상의 영향을 받아 고기압의 영향을 받는 동시에 상대습도의 변동성이 더 크며, 이에 따라 특정 시점에서 예측 성능이 저하되어 MAXAE가 상대적으로 크게 나타난 것으로 해석할 수 있다 (KMA 2025a). 제주의 RMS 오차는 0.034 m, MAE는 0.025 m로 제주의 기상 변화량은 4개 상시관측소 중에서 가장 작지만, 쿠로시오 난류의 영향을 받아 연중 온난 습윤하며 가장 큰 평균 상대습도를 가진다 (KMA 2025c). 그러한 해양성 난류의 영향으로 습도 변동성이 크지 않아 극단적 오차가 상대적으로 적게 발생하였다. 이에 따라 예측 오차는 대전, 속초에 비하여 크게 나타났음에도 불구하고, MAXAE는 0.177 m로 속초보다 작은 값을 보였다. 최대 ZWD 오차는 밀양에서 RMS 오차가 0.037 m로 가장 크게 나타났으며 이는 지역적 특성으로 인한 여름철 급격한 ZWD 변화 혹은 입력 데이터의 부재와 관련된 것으로 판단된다.
Table 4. Prediction error of ZWD for each KASI stations.
| Station | Mean (m) | STD (m) | RMS (m) | MAXAE (m) | MAE (m) |
|---|---|---|---|---|---|
| DAEJ | -0.000 | 0.029 | 0.029 | 0.164 | 0.020 |
| JEJU | 0.006 | 0.034 | 0.034 | 0.177 | 0.025 |
| SKCH | -0.003 | 0.030 | 0.030 | 0.215 | 0.020 |
| MLYN | 0.008 | 0.036 | 0.037 | 0.156 | 0.028 |
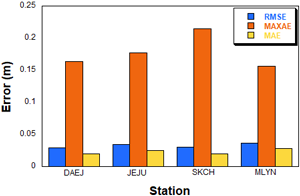
Fig. 13. ZWD prediction error for each KASI stations in 2022.
본 연구와 유사한 기존 논문을 비교 대상으로 삼아, 동일 국가 또는 본 논문에서 사용한 한반도와 유사한 ZWD 범위를 가지는 지역의 예측 결과를 검토하였다. MLP와 LSTM을 사용한 Lim & Bae (2021) 연구의 경우 LSTM 모델에서 0.0262 m 수준까지 RMS 오차를 줄였다. BPNN과 RF 모델을 사용한 Li et al. (2023) 연구의 경우 RF 모델의 경우 RMS 오차는 0.0353 m, BPNN 모델의 경우 0.0365 m RMS 오차를 달성하였다. CNN 모델을 사용한 Bi et al. (2024) 연구는 대기 모델에 따라 각각 0.0389 m, 0.0421 m의 RMS 오차를 달성하였으며, CNN-LSTM 모델로 예측한 Wu et al. (2024)의 연구에서는 0.0440 m의 RMS 오차를 달성하였다. 예측 정확도는 기법뿐만 아니라 입력 변수와 최적화 방법에 따라 크게 달라지는데, 본 연구는 단기 예측에 최적화된 파라미터를 적용하여 계절과 지역을 불문하고 안정적인 성능을 확보하였다.
GNSS 신호 지연의 주요 원인인 대류층 지연은 기상 변수와 계절 변화에 큰 영향을 받으며, 특히 ZWD는 수증기량과 지역적 기상 조건에 따라 변동성이 커 높은 예측 정확도가 필요하다. 본 연구에서는 LSTM 기반 예측 모델을 통해 ZWD를 예측하였으며, 5년간의 기상변수 시계열 데이터를 학습한 뒤 1년간의 예측 성능을 분석하였다. 모델 성능 검증을 위한 ZWD 참값으로는 PPP를 통해 추정된 ZTD와 UNB3m 모델을 통해 추정된 ZHD의 차이를 사용하였다.
예측 결과, 국내 지상국들의 예측 오차 RMS의 평균은 여름 (2022년 7월)에 0.049 m로 높았고, 겨울 (2022년 11월)에는 0.027 m로 낮아졌다. 이는 건조한 계절일수록 예측 오차가 낮게 유지되고, 습한 날씨에서도 기상 변동성을 비교적 잘 추적함을 의미한다. 2022년 전체 예측에서 대전과 속초의 예측 오차 RMS는 각각 0.029 m와 0.030 m, 제주는 0.034 m, 밀양은 0.037 m로, 네 지점 모두 유사한 오차 수준을 보였다. 이러한 결과는 LSTM 모델이 계절 및 지역에 관계없이 안정적인 성능을 유지하며, GNSS 대류층 지연 예측에 충분히 활용 가능함을 보여준다.
본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음 (과제번호 RS-2022-00207459).
Conceptualization, J.K.; formal analysis, S.Y. and Y.K.; data curation, S.Y. and Y.K.; writing—original draft preparation, S.Y. and Y.K.; writing—review and editing, J.K.; project administration, J.K., H.K.; funding acquisition, H.K.
The authors declare no conflict of interest.
Bergstra, J. & Bengio, Y. 2012, Random Search for Hyper-Parameter Optimization, Journal of Machine Learning Research, 13, 281-305.
Bevis, M., Businger, S., Herring, T. A., Rocken, C., Anthes, R. A., et al. 1992, GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system, Journal of Geophysical Research: Atmospheres, 92, 15787-15801. https://doi.org/10.1029/92JD01517
Bi, H., Huang, L., Zhang, H., Xie, S., Zhou, L., et al. 2024, A deep learning-based model for tropospheric wet delay prediction based on multi-layer 1D convolution neural network, Advances in Space Research, 73, 5031-5042. https://doi.org/10.1016/j.asr.2024.02.039
Brochu, E., Cora, V. M., & de Freitas, N. 2010, A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning, arXiv:1012.2599. https://doi.org/10.48550/arXiv.1012.2599
Chen, J. & Gao, Y. 2024, A Machine Learning-Based Tropospheric Prediction Approach for High-Precision Real-Time GNSS Positioning, Sensors, 24, 2597. https://doi.org/10.3390/s24102957
Cui, Z., Ke, R., Pu, Z., & Wang, Y. 2018, Deep Bidirectional and Unidirectional LSTM Recurrent Neural Network for Network-wide Traffic Speed Prediction, in International Workshop on Urban Computing (UrbComp), Nova Scotia, Canada, 14 Aug. 2017. https://doi.org/10.48550/arXiv.1801.02143
Hochreiter, S. & Schmidhuber, J. 1997, Long Short-Term Memory, Neural Computation, 9, 1735-1780. https://doi.org/10.1162/neco.1997.9.8.1735
Hofmann-Wellenhof, B., Lichtenegger, H., & Collines, J. 2001, GPS Theory and Practice, 5th ed. (New York: Springer-Verlag Wien).
Katsougiannopoulos, S. & Pikridas, C. 2009, Prediction of zenith tropospheric delay by multi-layer perceptron, Journal of Applied Geodesy, 3, 223-229. https://doi.org/10.1515/JAG.2009.022
Korea Meteorological Administration, Regional climate characteristics [Internet], cited 2025a Apr 28, available from: https://www.weather.go.kr/w/climate/statistics/regional-char.do
Korea Meteorological Administration, Korean climate characteristics [Internet], cited 2025b Apr 28, available from: https://www.weather.go.kr/w/climate/statistics/korea-char.do
Korea Meteorological Administration, Korean climate characteristics [Internet], cited 2025c Apr 28, available from: https://www.weather.go.kr/w/climate/statistics/regional-char.do?area=9
Li, Q., Yuan, L., & Jiang, Z. 2023, Modeling tropospheric zenith wet delays in the Chinese mainland based on machine learning, GPS Solutions, 27, 171. https://doi.org/10.1007/s10291-023-01507-4
Li, S., Xu, T., Xu, Y., Jiang, N., & Bastos., L. 2022, Forecasting GNSS Zenith Troposphere Delay by Improving GPT3 Model with Machine Learning in Antarctica, Atmosphere, 13, 78. https://doi.org/10.3390/atmos13010078
Lim, S.-H. & Bae, T.-S. 2021, Estimation of GNSS Zenith Tropospheric Wet Delay Using Deep Learning, Journal of the Korean Society of Surveying, Geodesy, Photogrammetry and Cartography, 39, 23-28. https://doi.org/10.7848/ksgpc.2021.39.1.23
Selbesoglu, M. O. 2020, Prediction of tropospheric wet delay by an artificial neural network model based on meteorological and GNSS data, Engineering Science and Technology, an International Journal, 23, 967-972. https://doi.org/10.1016/j.jestch.2019.11.006
Snoek, J., Larochelle, H., & Adams, R. P. 2012, Practical Bayesian Optimization of Machine Learning Algorithms, Advanced in Neural Information Processing Systems, 4. https://doi.org/10.48550/arXiv.1206.2944
Sutskever, I., Vinyals, O., & Le, Q. V. 2014, Sequence to sequence learning with neural networks, arXiv:1409.3215. https://doi.org/10.48550/arXiv.1409.3215
Wu, Y., Huang, L., Feng, W., & Tian, S. 2024, A Hybrid Deep Learning Algorithm for Tropospheric Zenith Wet Delay Modeling with the Spatiotemporal Variation Considered, Atmosphere, 15, 121. https://doi.org/10.3390/atmos15010121
Zaremba, W., Sutskever, I., & Vinyals, O. 2014, Recurrent neural network regularization, arXiv:1409.2329. https://doi.org/10.48550/arXiv.2329.1409