1School of Integrated Technology, Yonsei University, Incheon 21983, South Korea
2Time and Frequency Group, Korea Research Institute of Standards and Science, Daejeon 34113, South Korea
3Satellite System Laboratory, LIGNex1, Seongnam, Gyeonggi-do 13488, South Korea
Citation: Lee, H., Park, S., Rhee, J. H., Kim, G., Lee, C., et al. 2025, Comparison of Clock Drift Modeling Methods for Maintaining Time Synchronization Between GNSS Receivers, Journal of Positioning, Navigation, and Timing, 14, 313-319.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 313-319. https://doi.org/10.11003/JPNT.2025.14.3.313
Received on Aug 10, 2025, Revised on Aug 24, 2025, Accepted on Aug 25, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Precise time synchronization among distributed infrastructure is essential for enhancing the performance of systems such as wireless sensor networks, cellular base stations, and terrestrial navigation systems. Global Navigation Satellite System (GNSS) time transfer is a widely used method for synchronizing remote receivers; however, due to communication or operational constraints, it is often performed only intermittently at periodic intervals. During these intervals, clock offsets between receivers may accumulate due to clock drift and can lead to degraded time synchronization accuracy. To address this issue, this study evaluates and compares three clock drift modeling methods—moving average, polynomial fitting, and Kalman filtering—for predicting and compensating clock offsets between GNSS receivers in the absence of continuous GNSS time transfer. Both 2-state and 3-state Kalman filter models are considered to examine how the number of state variables affects prediction performance. Experiments were conducted using real data collected from two GNSS receivers: one disciplined by an external rubidium atomic clock and the other steered to GPST. The results show that when the GNSS time transfer interval is less than 20 hours, the 2-state Kalman filter achieves the best performance, whereas the 3-state Kalman filter performs better for longer intervals. These findings provide practical guidelines for selecting appropriate clock drift compensation strategies and GNSS synchronization intervals based on timing accuracy requirements and system constraints.
time synchronization, clock drift, GNSS time transfer, moving average, polynomial fitting, Kalman filtering
정밀한 시각 동기의 유지는 현대 사회의 다양한 기술 인프라가 안정적이고 정확하게 작동하기 위한 핵심 요소 중 하나이다. 예를 들어, 이동통신, 지상 항법 시스템, 센서 네트워크와 같은 응용 분야에서는, 분산된 기지국 또는 노드 간의 시각을 정밀하게 동기화함으로써 보다 높은 수준의 서비스 품질을 제공할 수 있다 (Sivrikaya & Yener 2004, Johannessen 2004, Kim & Seo 2023, Lee et al. 2024b, Kang et al. 2025).
지리적으로 떨어진 기지국 또는 노드 간의 시각을 동기화하는 대표적인 방법으로는 Global Navigation Satellite System (GNSS) 시각전송(time transfer) 기법이 있다 (Lewandowski et al. 1993, Lewandowski & Thomas 2002, De Lorenzo et al. 2010). 이 방식은 각 기지국에 GNSS 수신기를 설치하고, GNSS 위성 시각을 공통 기준으로 활용하여 수신기 간의 시각 차이를 추정 및 보정하는 방식이다. 대표적인 구현 방식으로는 두 수신기에 공통으로 보이는 위성만을 활용하는 common-view (CV)와, 수신기별로 관측 가능한 모든 위성을 사용하는 all-in-view (AV) 방식이 있다 (Weiss et al. 2005, Lee et al. 2008). 그러나 실제 시스템 운용 환경에서는 통신 자원 등의 제약으로 인해 GNSS 시각전송을 연속적으로 수행하기 어려우며, 일반적으로 일정한 주기에 따라 제한적으로 수행된다. 이러한 경우, 마지막 시각전송 이후 시간이 경과함에 따라 수신기에 연결된 시계의 오차가 점진적으로 누적될 수 있다.
이러한 문제를 보완하기 위해, GNSS 시각전송이 이루어지지 않는 구간에서는 수신기 시계의 시각 오차 변화 추세를 예측하고 보정할 수 있는 시계 오차(clock drift) 모델링 기법이 활용될 수 있다. 대표적인 기법으로는 이동 평균(moving average) (Xiong et al. 2015), 다항 회귀(polynomial fitting) (Huang et al. 2014, Wu et al. 2015), 칼만 필터(Kalman filter) (Galleani & Tavella 2003, 2010, Hauschild & Montenbruck 2009) 등이 있으며, 이들은 시계 오차의 시간적 변화를 모델링하여 향후 오차를 예측하고 보정하는 데 활용된다.
시계 오차의 특성은 시계의 종류에 따라 상이하게 나타나며, 본 연구에서는 루비듐 원자 시계에 동기된 GNSS 수신기를 대상으로, GNSS 시각전송 이후의 시각 동기 상태를 유지하기 위한 다양한 시계 오차 모델링 기법의 성능을 비교하였다. 각 기법에 대해 시각전송 주기와 경과 시간에 따른 시계 오차 보정 정확도를 정량적으로 평가하였다.
본 논문의 2장에서는 GNSS 수신기 간 시각 동기 방법과, 본 연구에서 적용한 시계 오차 모델링 기법들을 소개한다. 3장에서는 실험 환경 및 세팅을 설명하고, 4장에서는 실험 결과에 기반하여 각 기법의 성능을 비교 분석하였다. 마지막으로 5장에서는 본 연구의 결론을 제시한다.
Fig. 1은 지리적으로 떨어진 두 시계의 시각을 Global Positioning System (GPS) 시각전송을 통해 동기하는 과정을 개략적으로 나타낸다. 각 수신기(Fig. 1의 수신기 A와 B)는 GPS 위성으로부터 수신한 의사거리(pseudorange) 측정치를 이용해 GPS 시각(GPST)과 수신기에 연결된 시계와의 시각 차이를 산출한다. 이후 두 수신기가 해당 결과를 교환하면, GPST 대비 시각 오차의 차분을 통해 시계 A와 B 간의 시각차(clock difference)를 계산할 수 있다. 이 과정에서 이중주파수 측정치를 통한 전리층 지연 보정 등 추가적인 보정을 적용하면 동기 정확도를 향상시킬 수 있다 (Seo & Walter 2014, Lee et al. 2024a, 2025, Zhang et al. 2024).
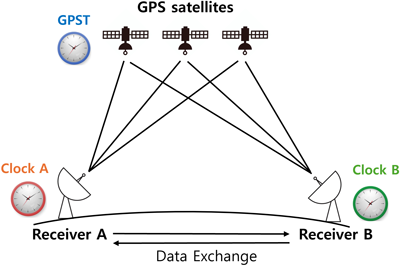
Fig. 1. Overview of the GPS time transfer between two remote receivers.
그러나 통신 자원 등 상황에 따라 시각 비교 데이터(CGGTTS)는 실시간으로 전송되기 어려울 수 있으며, 시각전송이 이루어지지 않는 구간에서는 수신기에 연결된 시계의 오차가 누적된다. 이러한 구간에서도 안정적인 동기를 유지하기 위해, 시계 오차의 변화를 예측하는 모델링 기법이 필요하다. 본 연구에서는 이동 평균, 다항 회귀, 칼만 필터 기반 기법을 적용하여 시계 오차를 예측하고 보정하였다. 다음 절부터는 각 모델링 기법에 대해 서술하였다.
이동 평균 (Xiong et al. 2015)은 시계열 예측에서 가장 단순하면서도 널리 사용되는 기법 중 하나이다. 이 방식은 과거 일정 구간의 값을 단순 평균하여 미래 시점을 예측하는 것으로, 복잡한 모델링 없이도 빠르게 추정값을 산출할 수 있는 장점이 있다. 본 연구에서는 과거 N개의 시점에서 측정된 수신기 간 시각차 값을 기반으로, 다음 시점의 값을 Eq. (1)과 같이 예측하였다.
$$\hat{x}_t
= \frac{1}{N}\sum_{i=1}^{N} x_{t-i}$$
여기서, $\hat{x}_t$는 시점 $t$에서의 시각차 예측값, $x_{t-i}$는 과거 시각차 관측값이며, $N$은 이동 평균 윈도우 길이를 의미한다 (본 논문에서는 $N=4$로 설정하였음). 이동 평균 방식은 구조가 단순하고 계산량이 적어 구현이 용이하며, 시각차 변화가 비교적 완만한 구간에서는 안정적인 예측 성능을 보인다. 그러나, 시계 오차에 급격한 추세 변화가 발생하거나, 이상치가 존재하는 경우에는 반응 속도가 느리다는 한계가 있다.
다항 회귀 (Huang et al. 2014, Wu et al. 2015)는 시간에 따라 변하는 데이터를 일정 차수의 다항식으로 근사하여 미래 값을 예측하는 방법이다. 특히, 데이터가 비교적 매끄러운 곡선 형태를 가질 경우 효과적으로 작동한다.
n차 다항식의 계수를 추정하기 위해서는 최소 n+1개의 관측값이 필요하다. 본 연구에서는 다항식의 최대 차수를 5차로 설정하되, 사용 가능한 관측값의 수에 따라 차수를 자동으로 조정하였다. 예를 들어, 관측값이 2개만 존재하는 경우에는 1차 다항식을 이용해 시계 오차를 모델링하고, 관측값이 6개 이상 확보되는 시점부터는 5차 다항식 모델을 적용하였다. 본 연구에서 사용한 5차 다항식 모델은 Eq. (2)와 같이 표현된다.
$$\hat{x}_t
= a_{5} t^{5}
+ a_{4} t^{4}
+ a_{3} t^{3}
+ a_{2} t^{2}
+ a_{1} t
+ a_{0}$$
여기서 다항식 계수인 $a_i$는 최소제곱법을 통해 추정하였다. 다항 회귀는 계산량이 적고 구현이 간단하지만, 고차 다항식을 사용할 경우 모델 데이터의 노이즈까지 과도하게 학습하는 과적합(overfitting)이 발생할 수 있다는 단점이 있다.
칼만 필터 (Galleani & Tavella 2003, 2010, Hauschild & Montenbruck 2009)는 선형 동적 시스템(linear dynamic system)의 상태(state)를 관측값으로부터 재귀적으로 추정하는 필터이다. 본 연구에서는 두 수신기 간 시각차 데이터를 바탕으로 시간 경과에 따른 시계 오프셋(clock offset)의 변화를 칼만 필터로 추정하였다.
특히, 본 연구에서는 칼만 필터의 상태 공간 모델(state-space model)을 두 가지 방식으로 설정하고, 이들의 성능을 비교하였다. 첫번째는 2차원 상태 벡터($x_t,\ \dot{x}_t$)를 사용하는 방식이며, 두번째는 3차원 상태 벡터($ x_t,\ \dot{x}_t,\ \ddot{x}_t $)를 사용하는 방식이다. 두 경우의 상태 벡터는 각각 Eqs. (3, 4)와 같이 정의된다.
$$\mathbf{x}_t
=
\begin{bmatrix}
x_t \\
\dot{x}_t
\end{bmatrix}$$
$$\mathbf{x}_t
=
\begin{bmatrix}
x_t \\
\dot{x}_t \\
\ddot{x}_t
\end{bmatrix}$$
여기서, $ x_t,\ \dot{x}_t,\ \ddot{x}_t $는 각각 시점 $t$에서의 시각차 오프셋(offset), 드리프트(drift), 드리프트 변화율(drift rate)을 나타낸다. 다음으로, 칼만 필터의 시스템 모델은 Eq. (5)와 같이 정의된다 (Galleani & Tavella 2003, Khodarahmi & Maihami 2023).
$$\mathbf{x}_t
=
\mathbf{A}\mathbf{x}_{t-1}
+
\mathbf{w}_t$$
여기서, $\mathbf{A}$는 상태 전이 행렬로, 2-state과 3-state 모델에 대해서 각각 Eqs. (6, 7)과 같이 정의된다 (Huang & Zhang 2012). $\mathbf{w}_t \sim \mathcal{N}(0, \mathbf{Q})$는 시스템 잡음 벡터이며, $\mathbf{Q}$는 시스템 잡음 공분산 행렬이다. 본 논문에서는 2-state과 3-state 모델에 대해서 각각 시스템 잡음 공분산 행렬을 $\mathbf{Q}=\text{diag}(10^{-3},10^{-3})$과 $\mathbf{Q}=\text{diag}(10^{-3},10^{-6},10^{-9})$로 설정하였다.
$$\mathbf{A}
=
\begin{bmatrix}
1 & \Delta t \\
0 & 1
\end{bmatrix}$$
$$\mathbf{A}=
\begin{bmatrix}
1 & \Delta t & \tfrac{1}{2}\,\Delta t^{2} \\
0 & 1 & \Delta t \\
0 & 0 & 1
\end{bmatrix}$$
또한, 칼만 필터의 관측 모델은 Eq. (8)과 같이 정의된다 (Galleani & Tavella 2003, Khodarahmi & Maihami 2023).
$$z_t = \mathbf{H}\,\mathbf{x}_t + v_t$$
여기서, $z_t$는 시점 $t$에서 관측된 수신기 간 시각차이며, $\mathbf{H}$는 관측 행렬로, 2-state과 3-state 모델의 경우에 대해 각각 $\mathbf{H}=[1 \:\: 0], \mathbf{H}=[1 \:\: 0 \:\: 0]$으로 정의된다. $ v_t \sim \mathcal{N}(0, R)$은 관측 잡음이며, $R$는 관측 잡음 분산으로, 관측 데이터를 바탕으로 추정하였다.
이러한 시스템 모델과 관측 모델을 바탕으로, 칼만 필터는 예측(prediction)과 업데이트(update) 단계를 반복 수행함으로써 시점 $t$에서의 상태 벡터를 추정한다. 예측 및 업데이트의 수식과 알고리즘에 대한 세부 내용은 선행연구 (Galleani & Tavella 2003, 2010, Hauschild & Montenbruck 2009)에 서술되어 있다.
본 연구에서는 두 대의 GNSS 수신기를 활용하여 실험을 수행하였다. 전체 실험 구성 및 데이터 처리 과정은 Fig. 2에 나타내었다.
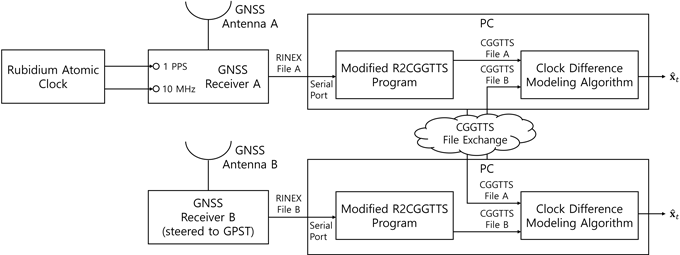
Fig. 2. Block diagram of the experimental setup and data processing flow.
루비듐 원자 시계의 특성을 독립적으로 분석하기 위해, 두 GNSS 수신기 중 하나는 외부 기준 시계(external reference clock)로 루비듐 원자 시계를 사용하여 동작 시키고, 다른 하나는 GPST에 스티어링(steering) 되도록 운용하였다. 또한, 각 수신기에서 생성된 RINEX 파일은 직렬 포트(serial port)를 통해 PC로 전송되게 하였다. PC에서는 우선 R2CGGTTS 프로그램을 이용하여 RINEX 파일을 시각 비교용 표준 형식인 CGGTTS 파일로 변환하였다. 이때, R2CGGTTS 프로그램의 데이터 생성 간격과 관련된 코드를 일부 수정하여 사용하였으며, 이에 대한 세부 내용은 본 절 후반부에서 설명한다.
생성된 CGGTTS 파일은 두 PC 간에 교환이 가능하다고 가정하였다. 본 연구에서는 편의상 두 수신기를 동일한 PC에 연결하여 사용하였으며, 이에 따라 별도의 통신 과정을 거치지 않고 동일 PC에 CGGTTS 파일을 기록하였다. 마지막으로, PC에서는 두 CGGTTS 파일을 입력으로 하여, 파일 교환이 이루어지지 않은 시점의 시각차 $\hat{x}_t$를 추정하는 알고리즘을 적용하였다.
실험 시 GNSS 수신기로는 Septentrio Polarx3eTR, 루비듐 원자 시계로는 SRS FS725를 사용하였다. 실험 기간 동안, 루비듐 원자 시계는 외부 동기 없이 자율적으로 운용하였다. GNSS 안테나로는 Leica AS10를 사용하였다. 수집된 데이터는 2025년 6월 27일 6시 30분부터 2025년 7월 6일 23시 54분까지 약 열흘 간의 데이터를 포함한다.
GNSS 시각전송을 수행하기 위해서, R2CGGTTS 소프트웨어를 활용하였다. R2CGGTTS 소프트웨어는 Royal Observatory of Belgium에서 개발한 시각 비교용 소프트웨어로, 전세계 주요 시각 표준 관련 기관에서 널리 활용되고 있다 (Defraigne & Martínez-Belda 2010, Jaldehag et al. 2019, Yu et al. 2015). R2CGGTTS 소프트웨어를 통해, GPS RINEX 파일로부터 CGGTTS 파일을 생성할 수 있으며, 이를 통해 GPST 기준 수신기 시계의 시각차를 획득할 수 있다. 본 연구에서는 GPS 이중주파수(L1, L2) 측정치를 이용하여 생성한 CGGTTS 파일을 사용하였다.
CGGTTS 표준 (Defraigne & Petit 2015)은 현재 16분 주기로 데이터를 생성하는 방식을 채택하고 있다. 구체적으로, 수신기 동기화를 위해 약 2분간 lock 과정을 수행한 후, 13분 동안 위성 신호 데이터를 저장하며, 마지막 1분은 데이터 처리 및 대기 시간으로 사용된다. 이러한 절차를 통해 1997년 10월 1일 00:02:00 (UTC)를 기준으로 하루에 총 89회의 데이터가 16분 간격으로 생성된다. 이 과정에서 데이터 저장 시작 시각은 매일 4분씩 앞당겨지며, 예를 들어 00:02:00, 00:14:00, 00:10:00, 00:06:00 순으로 조정된다.
본 연구에서는 15분 주기의 CGGTTS 출력을 가능하게 하기 위해 기존 스케줄링을 수정하였다. 구체적으로, R2CGGTTS Fortran 코드에서 수신기 lock 시간을 기존 2분에서 1분으로 단축하여 전체 주기를 16분에서 15분으로 조정하였으며, 위성 신호 데이터 저장 기간은 기존과 동일하게 13분으로 유지하였다. 또한, 항성일과의 정합을 위해 수행되던 저장 시작 시각의 4분 조정 절차를 제거함으로써 일정한 15분 간격의 데이터 생성을 보장하였다.
본 연구에서는 GPS에 의한 시각 비교 데이터(CGGTTS) 전송을 15분 간격으로 수행한 결과를 기준으로 하여, 각 시계 오차 모델링 알고리즘의 성능을 평가하였다. Fig. 3a는 시간에 따른 두 수신기 시계 간의 상대적 변화를, Fig. 3b는 15분 간격 GPS 시각전송 결과(Fig. 3a의 ‘GPS CV (15-min Interval)’)를 기준으로 각 모델링 기법의 시각차 추정값과의 차를 나타낸다. Table 1에는 GPS 시각전송으로 측정한 시각차 대비 각 알고리즘의 추정값에 대한 평균제곱오차(Mean Squared Error, MSE)를 정리하였다. Fig. 3과 Table 1에 제시된 실험에서는 GPS 시각 비교 데이터 활용이 1시간 주기로 이루어진다고 가정하였으며, 각 알고리즘은 시각전송 시점의 시각차 값을 기반으로, 그 이후 구간의 시각차를 예측하였다.
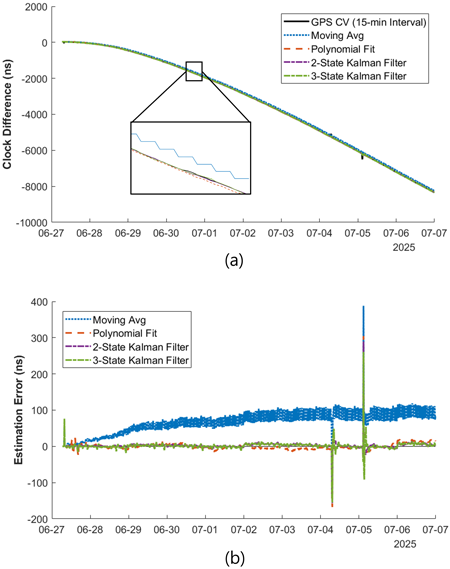
Fig. 3. (a) Predicted time difference between two receivers over time for each modeling algorithm, (b) Difference of each algorithm with respect to GPS common-view (CV) time transfer at 15-min intervals.
Table 1. MSE comparison of each algorithm at a GPS time transfer interval of 1 hour.
| Algorithm | Mean squared error (ns²) |
|---|---|
| Moving average | 5313.02 |
| Polynomial fitting | 187.08 |
| 2-state Kalman filter | 122.94 |
| 3-state Kalman filter | 130.70 |
Fig. 3과 Table 1의 결과에 따르면, GPS 시각전송 주기가 1시간일 경우, 2-state 칼만 필터가 가장 우수한 추정 성능을 보였다. 3-state 칼만 필터의 경우, 추정하는 상태가 한 개 늘었음에도 불구하고, 2-state 칼만필터에 비해 더 낮은 시각차 추정 정확도를 보였다. 시계의 drift rate까지 추정할 경우, 과적합이 발생하여 오히려 오차가 더 커진 것으로 판단된다.
본 연구에서는 GPS 시각 비교 데이터 전송 주기를 최소 30분에서 최대 30시간까지 설정한 뒤, 각 주기에 대한 각 알고리즘의 열흘 간의 평균제곱오차를 계산하였다. Fig. 4는 시각전송 주기에 따른 다항 회귀, 2-state 칼만 필터, 3-state 칼만 필터 기반 시계 오차 모델링 알고리즘의 평균제곱오차 변화를 나타낸다. 이동 평균 기반 시계 오차 모델링 기법은 Fig. 3과 Table 1에서 확인할 수 있듯이 다른 알고리즘에 비해 MSE가 현저히 크게 나타나므로, GNSS 시각 비교 데이터 전송 주기에 따른 최적 알고리즘을 비교·평가하는 Fig. 4에서는 제외하였다. Fig. 4a는 전체 구간(0~30시간)을, Fig. 4b는 0~12시간 구간을 확대하여 보여준다. 전체적으로 시각전송 주기가 짧을수록 시각 동기 정확도가 높았으며, 이는 모든 알고리즘에서 일관되게 관찰되었다. 예를 들어, 2-state 칼만 필터의 시각차 추정 MSE는 시각전송 주기가 30분일 때 114.2 ns2, 30시간일 때는 7931 ns2로, 주기가 길어질수록 오차가 점진적으로 증가하였다.
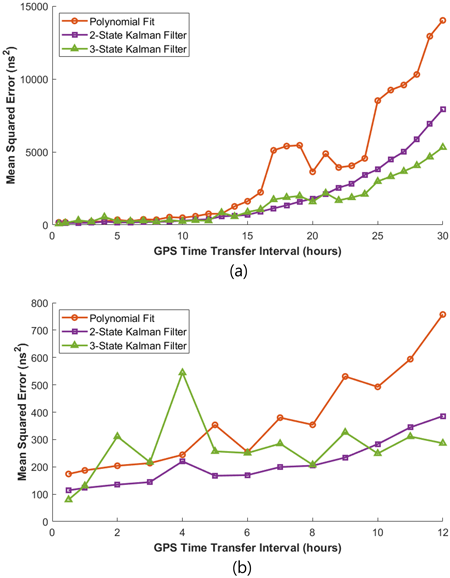
Fig. 4. (a) MSE of each algorithm as a function of the GPS time transfer interval, (b) Enlarged view of (a) for the interval range of 0–12 hours.
GPS 시각 비교 데이터 전송 주기가 20시간 미만인 경우에는 대체로 2-state 칼만 필터가 3-state 칼만 필터보다 우수한 성능을 보였으나, 주기가 20시간 이상으로 길어질 경우에는 3-state 칼만 필터가 상대적으로 더 나은 성능을 보였다. 일반적으로 3-state 칼만 필터는 시계 오차의 drift rate까지 추정하므로 과적합의 위험이 존재하지만, 시각전송 간격이 충분히 길어질 경우 시계의 고차원 동역학을 반영한 예측이 오히려 유리하게 작용할 수 있다. 따라서 장기 예측이 필요한 상황에서는 2-state 칼만 필터가 오히려 과소적합(underfitting)될 수 있으며, 이 경우 3-state 칼만 필터가 시계 오차를 더 정확하게 추정할 수 있는 것으로 분석된다.
실제 시스템 운용 시에는 요구되는 시각 동기 정확도과 통신 자원 제약 등을 고려하여 GNSS 시각전송 주기 및 예측 알고리즘을 적절히 선택할 필요가 있다. 예를 들어, 수십 나노초(ns) 수준의 정밀한 기지국 시각 동기가 필요한 경우에는 GPS 시각전송을 12시간 이내의 주기로 설정하고, 2-state 칼만 필터를 사용하여 시각 동기를 유지할 수 있다. 반면, 수 밀리초(ms) 수준의 동기 정확도로도 충분한 경우에는 3-state 칼만 필터를 적용하고, GPS 시각전송 주기를 수일 단위로 설정하여 통신 자원을 절감할 수 있다.
이동통신, 항법 시스템, 센서 네트워크 등 현대 사회의 다양한 인프라가 안정적으로 운용되기 위해서는 정밀한 시각 동기가 필수적이다. 이러한 인프라 간 시각 동기를 위한 대표적인 방법으로 GNSS 시각전송이 활용되지만, 실제 시스템 운용 환경에서는 통신 자원 등의 제약으로 인해 GNSS 시각전송이 자주 이루어지지 못하는 경우가 많으며, 이로 인해 시각 동기 성능이 저하될 수 있다. GNSS 시각전송이 이루어지지 않는 구간에서는 다양한 시계 오차 모델링 기법을 활용하여 시계 오차를 추정하고 보정함으로써 시각 동기 상태를 유지할 수 있다.
본 연구에서는 이동 평균, 다항 회귀, 칼만 필터의 세 가지 시계 오차 모델링 기법을 구현하고, 그 성능을 비교하였다. 특히 칼만 필터의 경우, 2차원 상태 벡터를 사용하는 2-state 모델과 3차원 상태 벡터를 사용하는 3-state 모델을 각각 구현하여 성능을 분석하였다. 실험은 각각 루비듐 원자 시계와 GPST를 기준으로 동작하는 두 GNSS 수신기로부터 수집한 실측 데이터를 바탕으로 수행하였다. 실험 결과, GNSS 시각전송 주기가 20시간 미만일 경우에는 2-state 칼만 필터가 가장 우수한 성능을 보였고, 20시간 이상일 경우에는 3-state 칼만 필터가 더 효과적인 것으로 나타났다.
이러한 결과는 실제 시스템 운용 시 요구되는 시각 동기 정확도와 통신 자원 제약 등을 고려하여, GNSS 시각전송 주기 및 예측 알고리즘을 적절히 선택하는 데 활용될 수 있다. 예를 들어, 수십 ns 수준의 정밀한 동기가 필요한 경우에는 2-state 칼만 필터와 짧은 전송 주기를 적용하고, 수 ms 수준의 시각 동기만으로도 충분한 경우에는 3-state 칼만 필터와 긴 전송 주기를 적용함으로써 시각동기 시스템의 효율적인 운용이 가능하다.
본 연구는 과학기술정보통신부의 재원으로 한국연구재단, 무인이동체원천기술개발사업단의 지원을 받아 수행되었음 (2020M3C1C1A01086407). 또한, 본 연구는 2024년 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행되었으며 (RS-2024-00407003, 지상파항법시스템 고도화 기술개발), 우주항공청의 재원으로 지원을 받아 수행된 것임 (과제번호: RS-2022-NR067078).
Conceptualization, H. Lee, S. Park, J. H. Rhee, G. Kim, C. Lee, and J. Seo; investigation, H. Lee, S. Park, and J. H. Rhee; resources, H. Lee and J. H. Rhee; writing—original draft preparation, H. Lee; writing—review and editing, H. Lee, S. Park, J. H. Rhee, G. Kim, C. Lee, and J. Seo; visualization, H. Lee; supervision, C. Lee and J. Seo; project administration, C. Lee and J. Seo; funding acquisition, J. Seo.
The authors declare no conflict of interest.
De Lorenzo, D. S., Lo, S. C., Seo, J., Chen, Y. H., & Enge, P. K. 2010, The WAAS/L5 Signal for Robust Time Transfer: Adaptive Beamsteering Antennas for Satellite Time Synchronization, In Proceedings of the 23rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2010), Portland, Oregon, 21–24 September 2010, p.2106–2116. https://www.ion.org/publications/abstract.cfm?articleID=9325
Defraigne, P. & Martínez-Belda, M. C. 2010, Galileo Common View: Format, Processing, and Tests with GIOVE, In Proceedings of the 42nd Annual Precise Time and Time Interval Systems and Applications Meeting, Reston, Virginia, 15–18 November 2010, pp.161–170. https://www.ion.org/publications/abstract.cfm?articleID=10730
Defraigne, P. & Petit, G. 2015, CGGTTS-Version 2E: an extended standard for GNSS Time Transfer, Metrologia, 52, G1. https://doi.org/10.1088/0026-1394/52/6/G1
Galleani, L. & Tavella, P. 2003, On the Use of the Kalman Filter in Timescales, Metrologia, 40, S326. https://doi.org/10.1088/0026-1394/40/3/312
Galleani, L. & Tavella, P. 2010, Time and the Kalman Filter, IEEE Control Systems Magazine, 30, 44–65. https://doi.org/10.1109/MCS.2009.935568
Hauschild, A. & Montenbruck, O. 2009, Kalman-Filter-Based GPS Clock Estimation for Near Real-Time Positioning, GPS Solutions, 13, 173–182. https://doi.org/10.1007/s10291-008-0110-3
Huang, G. & Zhang, Q. 2012, Real-Time Estimation of Satellite Clock Offset Using Adaptively Robust Kalman Filter with Classified Adaptive Factors, GPS Solutions, 16, 531–539. https://doi.org/10.1007/s10291-012-0254-z
Huang, G. W., Zhang, Q., & Xu, G. C. 2014, Real-Time Clock Offset Prediction with an Improved Model, GPS Solutions, 18, 95–104. https://doi.org/10.1007/s10291-013-0313-0
Jaldehag, K., Jarlemark, P., & Rieck, C. 2019, Further Evaluation of CGGTTS Time Transfer Software, In Proceedings of the 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum (EFTF/IFC), Orlando, FL, USA, 14–18 April 2019, pp.1–6. https://doi.org/10.1109/FCS.2019.8856022
Johannessen, S. 2004, Time Synchronization in a Local Area Network, IEEE Control Systems Magazine, 24, 61–69. https://doi.org/10.1109/MCS.2004.1275432
Kang, T., Park, S., Son, P.-W., & Seo, J. 2025, Enhancing eLoran Timing Accuracy via Machine Learning with Meteorological and Terrain Data, IEEE Access, 13, 112067–112080. https://doi.org/10.1109/ACCESS.2025.3581615
Khodarahmi, M. & Maihami, V. 2023, A Review on Kalman Filter Models, Archives of Computational Methods in Engineering, 30, 727–747. https://doi.org/10.1007/s11831-022-09815-7
Kim, W. & Seo, J. 2023, Low-Cost GNSS Simulators With Wireless Clock Synchronization for Indoor Positioning, IEEE Access, 11, 55861–55874. https://doi.org/10.1109/ACCESS.2023.3282786
Lee, H., Kim, S., Park, J., Jeong, S., Park, S., et al. 2024a, A Survey on New Parameters of GPS CNAV/CNAV-2 and Their Roles, Journal of Positioning, Navigation, and Timing, 13, 45–52. https://doi.org/10.11003/JPNT.2024.13.1.45
Lee, H., Kim, S., Park, J., Jeong, S., Yu, J., et al. 2025, A Comparative Survey of GPS Midi and Reduced Almanacs, Journal of Positioning, Navigation, and Timing, 14, 101–108. https://doi.org/10.11003/JPNT.2025.14.2.101
Lee, J., Oh, J.-I., Rhee, J. H., Choi, G. W., Lee, J. K., et al. 2024b, Study on a Method for Performance Evaluation and Analysis of TWSTFT Modems, Journal of Positioning, Navigation, and Timing, 13, 355–363. https://doi.org/10.11003/JPNT.2024.13.3.355
Lee, S. W., Schutz, B. E., Lee, C.-B., & Yang, S. H. 2008, A Study on the Common-View and All-in-View GPS Time Transfer Using Carrier-Phase Measurements, Metrologia, 45, 156. https://doi.org/10.1088/0026-1394/45/2/005
Lewandowski, W., Petit, G., & Thomas, C. 1993, Precision and accuracy of GPS time transfer, IEEE Transactions on Instrumentation and Measurement, 42, 474–479. https://doi.org/10.1109/19.278607
Lewandowski, W. & Thomas, C. 2002, GPS Time Transfer, Proceedings of the IEEE, 79, 991–1000. https://doi.org/10.1109/5.84976
Seo, J. & Walter, T. 2014, Future Dual-Frequency GPS Navigation System for Intelligent Air Transportation Under Strong Ionospheric Scintillation, IEEE Transactions on Intelligent Transportation Systems, 15, 2224–2236. https://doi.org/10.1109/TITS.2014.2311590
Sivrikaya, F. & Yener, B. 2004, Time Synchronization in Sensor Networks: A Survey, IEEE Network, 18, 45–50. https://doi.org/10.1109/MNET.2004.1316761
Weiss, M. A., Petit, G., & Jiang, Z. 2005, A Comparison of GPS Common-View Time Transfer to All-in-View, In Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition, Vancouver, BC, Canada, 29–31 August 2005, pp.324–328. https://doi.org/10.1109/FREQ.2005.1573953
Wu, Y., Zhu, X., Huang, Y., Sun, G., & Ou, G. 2015, Uncertainty Derivation and Performance Analyses of Clock Prediction Based on Mathematical Model Method, IEEE Transactions on Instrumentation and Measurement, 64, 2792–2801. https://doi.org/10.1109/TIM.2015.2418683
Xiong, L., Zhuo, F., Liu, X., Wang, F., & Chen, Y. 2015, Optimal Design of Moving Average Filter and Its Application in Distorted Grid Synchronization, In 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015, pp.3449–3454. https://doi.org/10.1109/ECCE.2015.7310147
Yu, D., Hwang, S., Lee, Y., Yang, S., & Lee, C. 2015, Analysis of the Ionospheric Effect for Time Offsets per GPS Code Measurements, International Journal of Software Engineering and Its Applications, 9, 77–86. https://www.earticle.net/Article/A252750
Zhang, R., Tu, R., Lu, X., He, Z., Guang, W., et al. 2024, Initial and Comprehensive Analysis of PPP Time Transfer Based on Galileo High Accuracy Service, GPS Solutions, 28, 94. https://doi.org/10.1007/s10291-024-01633-7