1Department of Geoinformatic Engineering, Inha University, Incheon 22212, Korea
2PP-Solution Inc., Seoul 08504, Korea
†Corresponding Author: Kwan-Dong Park, E-mail: kdpark@inha.ac.kr
Citation: Seol, Y., Rim, H.-J., Kim, Y.-G., & Park, K.-D. 2025, Real-Time Estimation of GPS Satellite Clock Offsets Using a Global Tracking Network and Analysis of GPS Block-Dependent Clock Biases, Journal of Positioning, Navigation, and Timing, 14, 211-220.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 211-220. https://doi.org/10.11003/JPNT.2025.14.3.211
Received on Aug 08, 2025, Revised on Aug 25, 2025, Accepted on Sep 05, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Centimeter-level precise positioning based on satellite navigation requires satellite clock offset accuracy at the nanosecond level, which is more precise than the time information provided by broadcast ephemeris. The development of precise realtime clock error estimation technology is therefore essential. This study developed a real-time Global Positioning System (GPS) satellite clock offset estimation algorithm based on a sequential filter. The algorithm estimates satellite clock offsets using data acquired from a global network of stations. The algorithm estimates the satellite clock offset, drift, receiver clock error, tropospheric zenith delay correction, and ambiguity parameters as state variables. The observation model uses un-differenced observations with an ionosphere-free combination technique. To improve the numerical stability of the Kalman filter, Cholesky decomposition and the Joseph stabilized form of the covariance update method were introduced. For validation, the results were compared with the final clock offset product from the Jet Propulsion Laboratory (JPL). The root mean square error (RMSE) was found to be 1.47 ns when using only carrier phase and 1.56 ns when using a combination of carrier phase and code. Additionally, a bias was observed depending on the GPS satellite block, with a magnitude reaching up to 2.5 ns.
GNSS, realtime estimation, satellite clock estimation, sequential filter
위성항법을 이용한 측위는 위치와 시각을 결정하는 핵심 요소로 궤도정보와 위성 시계 오프셋 정보가 활용된다. 궤도와 시각 정보의 정확도는 측위 정확도에 직접적으로 영향을 미치므로, 위성항법시스템이나 보강시스템의 성능은 정밀한 궤도 및 시각 정보를 제공하는 능력에 의해 결정된다.
위성에서 제공하는 방송궤도력의 궤도 정확도는 약 1D 평균 RMS 1 m 수준이며, 위성 시계 오프셋의 정확도는 약 Root Mean Square Error (RMSE) 5 ns(거리 환산 시 약 1.5 m)이다 (IGS, orbit and clock product 2025). 이러한 한계를 극복하기 위해 보다 정밀한 항법 정보를 제공하는 다양한 방법론이 제시되어 왔으며, 그중 State Space Representation (SSR) 방식이 널리 활용되고 있다. SSR은 위성 궤도오차, 위성 시계 오프셋, 전리층 대류층 지연 및 바이어스에 대한 오차항을 각각 보정정보로 제공하는 방식이다 (Lee & Park 2020, Shin et al. 2024).
SSR 보정 메시지 생성을 위해서는 단기간의 궤도를 정확히 예측하고 이를 기반으로 시계 오차를 실시간으로 추정하여야 한다. 전리층, 대류권을 비롯한 기타 오차항들은 앞서 생성한 궤도와 시각정보에 기반하여 추정된다.
국외에서는 이와 관련된 광범위한 선행 연구가 진행되어 왔다. Han & Jekeli (1998)는 위성과 시간에 대해 차분한 GPS 관측치를 사용하여 관측 모델을 단순화하여 30초 간격의 실시간 시각 추정을 수행하였다. 그리고 생성된 시각 정보를 이용한 측위 성능을 검증하여, 절대적인 GPS 시각 정보가 아닌 상대적인 시각 정보로도 고정밀 측위가 가능함을 증명하였다.
Hauschild (2011)는 차분되지 않은 관측을 활용한 실시간 시각 추정의 기본 원리를 제시하였다. 제시한 연구에서는 위성 탑재 시계에서 발생하는 불연속성(clock jump) 및 궤도 오차가 시계 오차 추정에 미치는 영향을 분석하였다. 이후 Galileo의 프로토타입인 Galileo In-Orbit Validation Element (GIOVE) 위성과 GPS 위성의 시계 오차를 동시에 추정하여 Precise Point Positioning (PPP)에 적용하고 Signal-in-Space Ranging Error (SISRE)를 분석함으로써 Galileo 위성 초기 단계의 시각 체계 구성에 기여하였다.
또다른 연구 동향으로는 다양한 위성군간의 호환성과 계산 효율성을 고려한 시각 추정 기법에 대한 연구가 활발히 진행되고 있다. Chen et al. (2021)은 Inter System Clock Bias (ISCB)를 시계 오차와 함께 추정하였다. 이 과정에서 에포크간 차분 관측치를 도입하여 계산의 복잡도와 모호정수에 의한 불확실성을 감소시켜 계산 효율성과 정확도가 개선되는 결과를 보였다.
실시간 시각 추정을 위한 추정기의 수치적 최적화 연구도 활발히 진행되고 있다. Zuo et al. (2021)은 실시간 정밀 시각 추정 과정에 Square Root Information Filter (SRIF)를 기반으로 추정잔차와 민감도 벡터에 기반한 이상값의 순차적 선택 및 제거 알고리즘을 적용하여 추정 결과의 정밀도와 계산 효율성이 개선됨을 보였다.
국내의 경우, GPS 위성의 정밀 궤도 결정에 대한 연구는 이루어졌지만 (Kim et el. 2024) 위성 시계 오프셋의 실시간 추정을 수행한 연구 사례는 확인되지 않는다. 그러나, 한국형 위성항법시스템의 개발 및 고정밀 보정정보의 국산화가 시도됨에 따라 실시간으로 정밀한 시각 정보를 생성하는 연구 또한 이루어져야 한다. 따라서, 본 연구는 실시간 시각 추정기의 프로토타입을 설계하는 것을 목적으로 한다. 제안하는 알고리즘은 전 지구 GNSS 관측망을 구성하여 IGS Real-time Service (RTS)를 이용해 관측 데이터를 실시간으로 제공받는다. 위성과 수신기의 좌표는 IGS와 Jet Propulsion Laboratory (JPL)의 최종 산출물을 이용해 고정한다. 이후, 데이터가 입력되는 매 에포크마다 비차분 관측치를 이용하여 GPS 위성 시계 오차를 순차적으로 추정한다.
이어지는 2장에서는 특정 조건에 따라 전 지구 관측망을 형성하고, 각 위성을 안정적으로 추적할 수 있는지 검증한다. 또한 본 알고리즘에서 사용되는 관측 모델과 추정하고자 하는 상태 변수를 정의한다. 3장에서는 GPS 위성 시계 오프셋의 오차 특성을 분석하고, 선형 칼만 필터의 설계와 자료처리 전략에 대해 설명한다. 4장에서는 처리 결과를 JPL 시계 오프셋 최종 산출물과 비교하며 위성 블록에 따른 오차 특성을 관측치의 종류와 연관 지어 분석한다. 마지막으로 5장에서는 4장의 결과로부터 결론을 도출하고, 향후 연구의 방향성에 대해 논의한다.
이번 장에서는 실시간 위성 시계 오프셋 추정을 위한 관측 정보 수집 과정과 추정 매개변수의 설계에 대해 다룬다. 2.1절에서는 전 지구 관측 데이터를 체계적으로 확보하기 위한 관측소 선정 전략과 데이터 수집 방법론을 제시한다. 2.2절에서는 시계 오프셋을 포함한 추정 매개변수의 설계 과정과 각 매개변수의 특성을 분석한다. 마지막으로 2.3절에서는 본 연구에서 사용되는 관측 방정식과 이론적 배경을 제시하고, 실제 추정 과정에서의 적용 방식을 상세히 설명한다.
GPS 32기 위성의 시계 오프셋을 연속적으로 추정하기 위해서는 전 지구에 균등하게 분포된 관측망 구축이 필수적이다. IGS 네트워크 (IGS, network 2025)에 따르면 2025년 5월 1일 기준 전 세계에 522개의 관측소가 운용 중이며, 이 중, 다음 단락에서 기술하는 선정 기준을 적용하여 66개의 관측소를 최종 선정하였다.
관측소 선정 기준은 다음과 같다. 첫째, 안정적인 시각 추정을 위해 H-maser, Cesium 또는 Rubidium 외부 원자시계를 장착한 관측소를 우선적으로 선정하였다. 이러한 조건을 만족하는 관측소는 전체 522개소 중 139개소이다. 둘째, 첫 번째 기준을 만족한 139개소 중에서 데이터 수집 기간인 2025년 DOY 005~007일(3일간) 동안 관측소가 정상 운영 상태를 유지하고 관측 파일이 안정적으로 제공된 관측소로 범위를 축소하였다. 셋째, 수신기 시계의 안정성을 고려하였다. 일부 수신기 시계는 Fig. 1과 같이 급격한 시계 조정을 보인다. 이러한 불연속적인 시계 패턴은 순차 필터 기반 추정 과정에서 필터의 수렴성과 추정 성능을 저해할 수 있으므로 이러한 패턴을 보이는 관측소는 제외하였다.

Fig. 1. Time series of receiver clock offsets for BOGI (2025 DOY 005) and CEDU (2025 DOY 005–007), obtained from the CODE final clock product and interpolated at 1-second intervals.
그 결과 59개의 관측소가 조건을 만족하였다. 마지막으로, GPS 위성이 궤도상에서 이동하는 동안 항상 최소 5개 이상의 관측소에서 관측될 수 있도록 하는 조건을 만족해야 한다. 하지만, 원자시계 위주로 선정된 관측망은 유럽과 북미 대륙에 편중되어 분포하고 있으며, 남태평양과 인도양 일대에는 관측소가 희소하게 분포하는 공간적 불균형이 존재한다. 이러한 지역적 관측 공백을 보완하기 위해 외부로 연결된 원자시계가 없지만 안정적인 내부 시계를 가진 7개소의 관측소를 추가하였으며, 최종적으로 66개소의 관측소를 선정하였다.
Fig. 2는 선정한 66개 관측소의 분포를 나타내고 있다. 컬러바는 궤도 반경 26,578.137 km, 경사각 55°의 원궤도를 가정한 GPS 위성이 위치할 수 있는 구면상의 모든 점에서 몇 개의 관측소에 동시에 관측될 수 있는지를 나타낸 것이다. Fig. 3은 단일 위성이 72시간 동안의 궤도 운동 과정에서 위성을 관측하는 관측소 수의 변화를 시간에 따라 보여준다. Figs. 2, 3에 따르면, 각 위성은 통과하는 지역의 관측소 분포에 따라 가시성의 편차가 확인되나 남인도양과 남태평양 상공과 같이 관측소가 희박하게 분포된 지역을 통과할 때도 최소 6개 이상의 관측소에 의해 관측되도록 관측망을 구성하였다.

Fig. 2. Distribution of the observation network. The markers indicate the type of clock. The color bar represents the number of stations that can simultaneously observe a satellite at any position satisfying the GPS orbital conditions (elevation mask 10° is adopted).
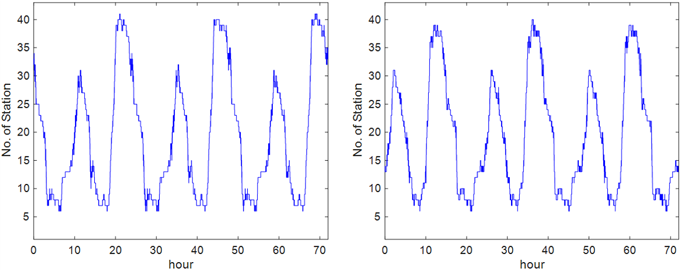
Fig. 3. Time series of the number of ground stations in contact with GPS satellite PRN02 (left) and PRN25 (right) over a 72-hour period (2025 DOY 005–007).
GPS 항법 메시지는 위성 시계 오프셋을 $a_0,\; a_1,\; a_2$ 3개의 매개변수를 통해 2차 다항식으로 모델링 하고 있다. 이는 GPS 위성 시계 오프셋의 시간에 따른 변화 양상이 2차함수에 근사함을 의미한다. 이러한 특성은 GPS 위성 시계 오프셋에서 2차 추세를 제거한 결과를 통해서도 확인할 수 있다. Fig. 4는 GPS 위성의 시계 오프셋을 1차 및 2차 다항식에 접합하여 시간적 추세를 제거한 후의 잔차를 나타낸 것이다. 위성 블록별로 차이가 확인되지만 2차 추세 제거 후의 잔차가 백색 잡음에 가까운 결과를 보이며 이는 2차 함수에 근사함을 의미한다.
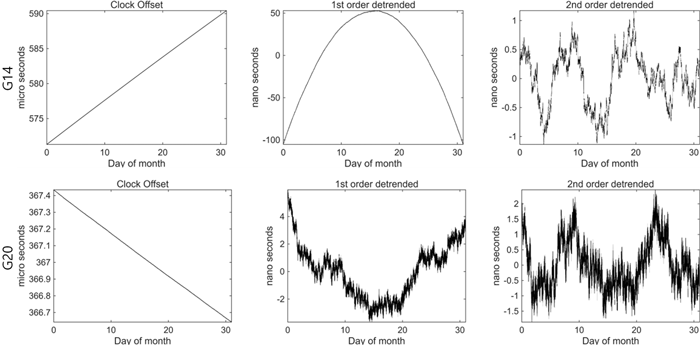
Fig. 4. First- and second-order detrended clock offsets of GPS satellites PRN14 (Block III) and PRN20 (Block IIR) during May 2025.
Eq. (1)은 GPS 항법 메시지를 이용해 위성 시계 오프셋을 계산하는 방법이다 (Anthony 2022). Eq. (1)에서 $dt_s$는 항법 메시지를 이용해 계산한 위성 시계 오프셋을, $t$는 사용자의 시각을, $t_{oe}$는 궤도력 기준 시각을 나타내며 $a_0$, $a_1$, $a_2$는 각각 위성 시계의 오프셋, 드리프트, 드리프트 변화율을 의미한다.
$$
d t_{s}
=
a_{0}
+
a_{1}(t – t_{oe})
+
a_{2}(t – t_{oe})^{2}
$$
여기서, 드리프트 변화율의 크기는 0에 근사한다. 그러므로 본 연구에서는 추정기의 복잡도를 낮추고자 2차 항, 즉, 드리프트 변화율 항은 생략하였고, 오프셋 및 드리프트 만을 추정하였다. 따라서 위성 시계 오프셋은 Eq. (2)와 같이 모델링 된다.
$$
\delta t_{s}^{\,t+1}
=
\delta t_{s}^{\,t}
+
\tau \cdot \dot{\delta t}_{s}^{\,t}
$$
여기서 $\delta t_s,\; \dot{\delta t}_s$는 본 연구에서 추정하는 위성시계 오프셋 및 드리프트를, $τ$는 순차 필터의 시간 간격을 의미하며, 본 연구에서는 30초 간격 관측 데이터를 사용하였기에 이를 30초로 설정하였다($τ$=30s). 위성 시계 오프셋을 제외한 나머지 상태 변수(수신기 시계 오프셋, 천정방향 대류권 지연량, 모호정수)는 각 하나의 항으로 모델링 하였다.
본 연구에서는 이온층에 의한 1차 오차를 제거하기 위해 Eq. (3)과 같이 무전리층 조합을 적용하였다 (ESA Navipedia 2025).
$$\begin{align}
\rho_{IF}
&=
\frac{f_{1}^{2}}{f_{1}^{2} – f_{2}^{2}} \cdot \rho_{1}
–
\frac{f_{2}^{2}}{f_{1}^{2} – f_{2}^{2}} \cdot \rho_{2}
\nonumber
\\[6pt]
\Phi_{IF}
&=
\frac{f_{1}^{2}}{f_{1}^{2} – f_{2}^{2}} \cdot \Phi_{1}
–
\frac{f_{2}^{2}}{f_{1}^{2} – f_{2}^{2}} \cdot \Phi_{2}
\end{align}$$
여기서, $\rho,\; \Phi,\; f$는 각각 코드의사거리 및 반송파 위상 관측치, 그리고 주파수를 의미하며 아래 첨자는 신호의 종류를 의미한다. 또한, IGS를 비롯한 여러 GNSS 처리기관은 산출물을 생성할 때, P1 및 P2 신호의 무전리층 조합 관측치를 기준으로 한다. 따라서, 본 연구 또한 GPS의 P1(C1W/L1W) 및 P2(C2W/L2W) 신호를 무전리층 조합하여 JPL 시계 오프셋 최종 산출물과 정렬하였다.
그러나, 관측망에서 사용되는 수신기 중 Trimble과 Leica의 일부 기종은 P2 신호를 수신하지 않는다. 15개 관측소가 이에 해당하며, Eq. (4)와 같이 C1 코드 의사거리(C1C) 관측에 Differential Code Bias (DCB)를 적용하여 사용하였다. 따라서, 코드의사거리 및 반송파 위상 관측 방정식은 Eqs. (5, 6)과 같이 유도된다.
$$
\rho_{P1}
=
\rho_{C1}
+
DCB_{(P1 – C1)}
$$
$$\rho_{IF}
=
\left| \mathbf{r}_{n} – \mathbf{r}^{s} \right|
+ c(\delta t_{r} – \delta t_{s})
+ c \cdot \delta_{\mathrm{rel}}
+ \delta_{\mathrm{trop}}
$$
$$\Phi_{IF}
=
\left| \mathbf{r}_{n} – \mathbf{r}^{s} \right|
+ c(\delta t_{r} – \delta t_{s})
+ c \cdot \delta_{\mathrm{rel}}
+ \delta_{\mathrm{trop}}
+ PWU
+ \lambda_{IF} \cdot N_{IF}
$$
여기서, $\mathbf{r}_n$과 $\mathbf{r}^s$는 각각 수신기와 위성의 위치 벡터이며, $\delta_{rel}$은 상대성 효과에 의한 보정, $\delta_{trop}$은 대류권에 의한 총 지연량, PWU는 phase wind up effect를 의미한다. 이 때, 관측 방정식의 일부 요소는 Eqs. (7-11)과 같이 세분하여 표현할 수 있다. Eq. (7)은 수신기 시계 오프셋 항의 구성이다.
$$d t_{r} = \widetilde{d t_{r}} + b_{\mathrm{rcv}}
$$
여기서 $\widetilde{dt}_{r}$은 바이어스가 포함되지 않은 수신기 시계 오프셋을, $b_{rcv}$는 수신기 DCB를 의미한다. 수신기 또한 위성과 동일하게 채널에 따른 DCB가 존재한다. 본 연구에서는 Eq. (7)과 같이 바이어스를 포함한 수신기 시계 오프셋을 추정하였다.
수신기와 위성의 위치 벡터($r_n, r^s$) 또한 여러 보정항으로 구성되어 있으며 Eqs. (8, 9)는 이의 구성을 나타낸다.
$$
\mathbf{r}_{n}
=
\tilde{\mathbf{r}}_{n}
+
\Delta \mathbf{r}_{\mathrm{ecc}}
+
\Delta \mathbf{r}_{ET}
+
\Delta \mathbf{r}^{rcv}_{ant}
$$
$$
\mathbf{r}^{s}
=
\tilde{\mathbf{r}}^{\,s}
+
\Delta \mathbf{r}^{sat}_{ant}
$$
여기서, $\tilde{\mathbf{r}}^{\,n}$은 Solution (software/technique) Independent Exchange format (SINEX)에서 제공되는 마커의 좌표, $\tilde{\mathbf{r}}^{\,s}$는 SP3에서 제공되는 위성 질량중심의 좌표를 의미하며 $\Delta r_{ecc}$는 수신기 좌표의 이심(eccentricity), $\Delta r_{ET}$은 지구 조석에 의한 효과, $\Delta r_{ant}^{rcv}$ 및 $\Delta r_{ant}^{sat}$ 은 위성과 수신기 안테나의 위상 중심 오프셋을 뜻한다.
대류권 총 지연량은, 경험적 모델을 통해 계산할 수 있는 오차와 추정되어야 하는 오차로 구성되어 있다. Eq. (10)은 그 구성을 나타낸다.
$$
\delta_{trop}
=
\delta_{ZHD}\cdot m_{fh}
+
\delta_{ZWD}\cdot mf_{w}
\qquad\text{where,} \;
\delta_{ZHD}
=
\tilde{\delta}_{\mathrm{ZHD}}
+
\varepsilon
$$
여기서, $\delta_{ZHD}$및 $\delta_{ZWD}$는 각각 천정방향 건조 및 습윤 대기에 의한 지연량을 의미하며, $mf_h$ 및 $mf_w$는 이에 대한 사상함수이다. $\delta_{ZHD}$는 경험적 모델인 Saastamoinen 모델 (Saastamoinen 1972)을 통해서 모델링 할 수 있는 부분($\tilde{\delta}_{ZHD}$)과, 잔여 오차($\varepsilon$)로 나뉜다. 따라서 $\delta_{trop}$은 Eq. (11)과 같이 나타낼 수 있다.
$$
\delta_{trop}
=
\left( \tilde{\delta}_{ZHD}+ \varepsilon \right) \cdot mf_{h}
+
\delta_{ZWD} \cdot mf_{w}
$$
여기서, $mf_h$와 $mf_w$ 는 Global mapping function (Boehm et al. 2006)을 통하여 계산할 수 있으며, 두 사상함수는 모두 위성의 고도각에 따라 천정방향 성분을 사선방향 성분으로 투영시키는 역할을 한다. 그러므로 ε를 추정할 때 $mf_h$ 대신 $mf_w$를 적용하여도 $\delta_{trop}$을 복원하는데 영향을 미치지 않는다. 따라서, Eq. (11)은 Eq. (12)와 같이 정리된다.
$$
\delta_{\mathit{trop}}
= \tilde{\delta}_{\mathit{ZHD}} \cdot mf_{h}
+ \left( \delta_{\mathit{ZWD}} + \varepsilon \right) \cdot mf_{w}
$$
본 연구에서는 상태벡터의 차원을 줄이고 추정기의 효율성을 높이기 위해 $\delta_{ZWD}$와 $\varepsilon$를 합하여 수직방향 지연 보정량(tropospheric zenith delay correction)으로 추정하였다. 최종적으로, $\delta_{trop}$은 Eq. (13)과 같이 모델링된다.
$$\delta_{\text{trop}}
=
\tilde{\delta}_{\mathrm{ZHD}} \cdot m f_h
+
\delta_{\mathrm{ZDC}} \cdot m f_w
\quad\text{where,} \;
\delta_{\mathrm{ZDC}}
=
\delta_{\mathrm{ZWD}}
+
\varepsilon$$
여기서, $\delta_{ZDC}$는 수직방향 지연 보정량을 의미하며, 이는 각 관측소에 대해 추정된다.
마지막으로, Eq. (14)는 반송파 위상 관측에 무전리층 조합을 적용하였을 때 모호정수 항의 구성이다.
$$\lambda_{IF} \cdot N_{IF}
=
\frac{f_1^{2}}{f_1^{2} – f_2^{2}} \cdot \lambda_{1} N_{1}
–
\frac{f_2^{2}}{f_1^{2} – f_2^{2}} \cdot \lambda_{2} N_{2}$$
여기서, $\lambda$, $f$는 각각 파장과 주파수를 의미하고 $N$은 모호정수를 뜻하며, 아래 첨자는 무전리층 조합에 사용하는 밴드를 나타낸다. 이 때, $N_1$과 $N_2$는 정수성을 띄고 있으나, 무전리층 조합 과정을 거친 $N_{IF}$는 정수성을 잃게 된다. 따라서 본 연구에서는 모호정수를 고정하지 않고 실수 상태로 추정하였다.
이번 장은 선형 칼만 필터(이하 ‘칼만 필터’)의 구성에 대한 내용을 담고 있다. 3.1절에서는 칼만 필터가 추정하고자 하는 미지수인 상태변수를 어떻게 설정하였으며 각 변수들 간에 확률적 특성을 부여하였는지 기술한다. 3.2절은 시각 데이텀 설정과 이를 위한 제약 조건에 대해 설명한다. 이후 3.3절에서는 칼만 필터의 일부 과정을 변형하여 고차원 실시간 구동 환경에서의 안정성을 향상시킨 방법을 소개한다.
본 알고리즘에서 상태 변수로써 추정되는 항은 Eqs. (2, 5, 6)의 $\delta t_s$, $\dot{\delta t}_s$, $\delta t_r$, $ZDC$, $N_{IF}$에 해당된다. 이 때, 32기의 GPS 위성과, 66개소의 관측소를 사용하였다. 따라서, 총 미지수의 개수는 Table 1과 같이 총 2308개로 결정된다.
Table 1. The total number of estimated unknowns.
| Unknowns | n (number of satellites) = 32 m (number of stations) = 66 | |
|---|---|---|
| $\delta t_s$ (Sat. clock offset) $\dot{\delta t}_s$ (Sat. clock drift) $\delta t_r$ (Rcv. clock offset) $ZDC$ (Tropospheric zenith delay correction) $N_{IF}$ (Ambiguity) | 𝑛 𝑛 𝑚 𝑚 𝑛 × 𝑚 | 32 32 66 66 2112 |
| Total | 2308 | |
또한, 상태 벡터 $\mathbf{X}$는 Eq. (15)와 같이 설계할 수 있으며, 위 첨자 $n$, $m$은 위성과 관측소에 각각 할당된 번호이다. 이 때, 위성 시계 오프셋 항과 위성 시계 드리프트 항은 1차 미분 관계를 가지며, 상태전이 행렬은 이를 반영해야 한다. Eq. (16)은 상태전이 행렬의 구성과 순차 필터의 예측 단계이다.
$$X =
\bigl[
\delta t_{s}^{1}\ \ldots\ \delta t_{s}^{n},\
\dot{\delta t}_{s}^{1}\ \ldots\ \dot{\delta t}_{s}^{n},\
\delta t_{r}^{1}\ \ldots\ \delta t_{r}^{m},\
ZDC^{1}\ \ldots\ ZDC^{m},\
N_{IF}^{1}\ \ldots\ N_{IF}^{ (n \times m)}
\bigr]^{T}$$
$$\begin{bmatrix}
\delta t_{s}^{n} \\
\dot{\delta t}_{s}^{n}
\end{bmatrix}^{t+1}
=
A_{\delta t_s}
\begin{bmatrix}
\delta t_{s}^{n} \\
\dot{\delta t}_{s}^{n}
\end{bmatrix}^{t}
\quad\text{where}\quad
A_{d t_s}
=
\begin{bmatrix}
1 & \Delta t \\
0 & 1
\end{bmatrix}$$
여기서, $A_{dt_s}$는 상태변수 $\delta t_s$와 $\dot{\delta t}_{s}$에 대한 상태전이행렬을 의미하며, 위 첨자는 각 에포크를 의미한다. 순차 필터의 시간 간격을 고려하여 비대각 성분을 설계하였으며, 이외의 상태변수들에 대한 상태전이행렬은 단위행렬($I$)로 구성된다.
상태변수가 실제 변수의 변화 특성을 정확히 반영하고, 추정 성능과 신뢰성을 극대화하기 위해서는 상태 변수에 대해 적절한 잡음 모델을 정의해야 한다. 본 연구에서는 위성 시계 오프셋이 장 단기적으로 어떠한 종류의 잡음 특성을 가지는지 분석하기 위해 Modified Allan Deviation을 사용하였다. Fig. 5는 GPS 위성의 시계 오프셋의 Averaging time에 따른 Modified Allan Deviation을 나타낸 것이다.
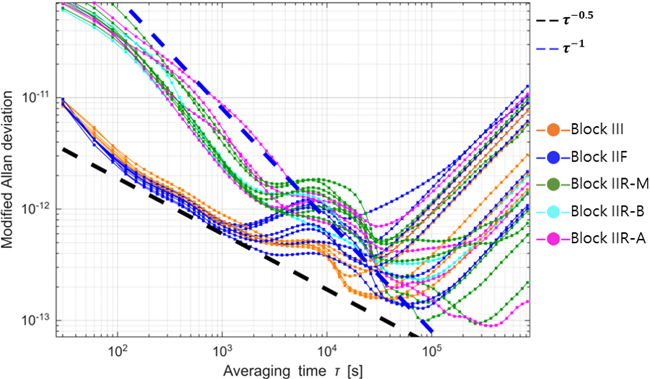
Fig. 5. Modified Allan deviation of the satellite clock offset collected during May 2025. Each line represents an individual GPS satellite, and the color indicates the satellite block type. The dashed reference lines correspond to slopes of τ-0.5 and τ-1, respectively.
Fig. 5에서 GPS 위성 시계는 블록별로 서로 다른 잡음 특성이 확인된다. 블록 III와 IIF는 단기 구간$(\tau < 10^3 s)$에서 $\tau^{-0.5}$ 기울기를 나타내어 random walk phase noise가 지배적임을 확인하였으며 블록 IIR 계열(IIR-A, IIR-B, IIR-M)은 동일 구간에서 $\tau^{-1}$ 기울기를 보여 flicker phase noise가 우세하게 나타났다 (IEEE 1998). 따라서, 블록 III와 IIF에는 random walk phase 모델을, IIR 계열에 대해서는 flicker phase와 random walk의 혼합 모델을 적용하는 것이 물리적으로 정확하나 본 연구에서는 계산 복잡도와 효율성을 고려하여 모든 GPS 위성 시계 오프셋 및 드리프트를 random walk로 모델링하였다. 이 때, 오프셋과 드리프트는 1차 미분 관계로 완전히 독립적이지 않으며 실제 시계는 물리적인 장치이기 때문에, 온도, 진동, 드리프트 변화율에 따라 오차 특성의 상관성이 발생할 수 있다 (Fernández et al. 2017). 따라서 이를 고려하여 process noise variance-covariance 행렬 $Q$를 Eq. (17)과 같이 모델링 하였다 (Swift 1987). 각 상태변수에 대해 부여한 process noise variance-covariance는 Hauschild (2011)에서 제시한 수치를 참고하였다.
$$Q =
\begin{bmatrix}
q_{1}\Delta t + q_{2}\frac{\Delta t^{3}}{3} &
q_{2}\frac{\Delta t^{2}}{2} \\
q_{2}\frac{\Delta t^{2}}{2} &
q_{2}\Delta t
\end{bmatrix}
\quad\text{where}\quad
q_{1}=\sigma_{\mathrm{offset}}^{2},\
q_{2}=\sigma_{\mathrm{drift}}^{2}$$
Liu et al. (2019)와 Zhang et al. (2011)의 실시간 시각 추정 및 PPP에 대한 선행 연구는 수신기 시계 오프셋을 white noise로 모델링 하였다. 그러나 본 연구에서 사용한 전 지구 관측망은 대부분 외부 원자시계를 장착한 관측소로 구성되어 있으며, 시계의 상태가 안정적인 관측소만을 사용하였기에 위성 시계 오프셋 및 드리프트와 동일하게 random walk로 모델링 하였다. ZDC는 시간에 따른 변화율이 매우 작은 값이기에 1시간 단위의 piecewise-constant로 모델링 하였다. 마지막으로, 모호정수는 위성-수신기간 각 관측쌍에 대해 constant로 모델링 하였고, set-rise 또는 사이클 슬립 이벤트가 발생하였을 때 초기화 하였다.
위성 시계 오프셋을 추정하기 위해서는 기준 시각과, 특이성(singularity) 문제를 고려해야 한다. 이 문제는 위성 및 수신기 시계 오프셋이 상대적으로만 결정되는 관측 방정식의 구조에서 발생한다. 따라서 시각의 절대적인 영점이 결정되지 않을 경우, 각 시각과 관련된 파라미터들은 무한한 상관관계를 갖게 되므로 랭크 결손(rank deficiency)이 발생한다. 이러한 문제를 해결하기 위해서는 기준 시계를 도입하여 그 값을 0 또는 임의의 상수로 고정하는 제약 조건을 부여해야 한다. 선행 연구에서 사용해온 방법으로는 GPS time과 근사한 한 개의 지상 시계를 고정하거나, 한 개의 위성 시계를 고정한 후 방송궤도력 시각 정보를 통해 복원하는 기법이 제시되어 왔으며 (Maciuk & Lewińska 2019), zero-mean condition을 부여하는 방법 또한 제시되어 왔다 (Huang et al. 2021). 이로써 모든 시계 오프셋들은 설정한 기준에 대해 상대적으로 정의되며, 파라미터 간 일관성이 확보된다. 만약 지상 시계 1기를 기준 시계로 고정한다면, 필터의 추정 안정성은 연결된 수신기의 수신 안정성에 영향을 받는다. 따라서, 더욱 안정적으로 유지되는 위성 시계를 이용해 제약을 주는 방식이 권장된다 (Rovira‑Garcia et al. 2021). 본 연구는 zero-mean condition을 응용하여, Eq. (18)과 같이 추정한 위성 시계 오프셋의 평균이 방송궤도력을 통해 제공되는 시계 오프셋의 평균과 일치하도록 제약을 하였다.
$$\frac{1}{n}\sum_{k=1}^{n} \delta t_{s}^{k}
=
\frac{1}{n}\sum_{k=1}^{n} d t_{s}^{k}$$
여기서, $n$은 사용 가능한 위성의 수, $dt_s^k$ 는 Eq. (1)과 같이 방송궤도력을 통해 산출한 위성 $k$의 시계 오프셋을 의미한다.
본 연구에서는 추정기로써 칼만 필터를 사용하였다. GNSS 측정치가 노이즈를 포함하거나 불완전한 경우에도 예측과 갱신 단계를 통해 추정하고자 하는 변수들을 실시간으로 추정할 수 있다. 특히, 칼만 필터는 낮은 지연 시간으로 작동하며 일시적인 수신 불량 등의 이유로 관측 간격이 불규칙해지는 상황에서도 강건한 추정 성능을 보장하므로 GNSS 데이터의 실시간 처리에 적합하다. 칼만 필터가 상태 벡터와 분산-공분산 행렬에 대해 예측 및 갱신을 수행하는 과정은 Eqs. (19-22)과 같다 (Grewal & Andrews 2015).
$$\begin{align}
\hat{x}_{k}^{-} &= A\, \hat{x}_{k-1} \notag \\
P_{k}^{-} &= A P_{k-1} A^{T} + Q
\end{align}$$
$$K_k = P_{k}^{-} H^{T} \left( H P_{k}^{-} H^{T} + R \right)^{-1}$$
$$\hat{x}_{k}
=
\hat{x}_{k}^{-}
+
K_{k}\left( z_{k} – H\hat{x}_{k}^{-} \right)$$
$$P_{k} = P_{k}^{-} – K_{k} H P_{k}^{-}$$
여기서, $\hat{x}_{k}$는 시간 $k$에서 추정된 상태벡터를 의미하며, $\hat{x}_{k}^{-}$는 관측값이 반영되기 전의 예측 상태 벡터를 의미한다. $A$는 상태전이 행렬을, $P_k$는 $k$에서의 상태 추정 오차 공분산 행렬을 나타내며 $P_k^-$는 관측이 반영되기 전의 예측된 공분산 행렬이다. $Q$는 시스템 잡음의 공분산 행렬을 나타내고, $K_k$는 칼만 이득을, $H$는 설계 행렬을 나타낸다. $z_k$는 시간 $k$에서의 실제 관측값을 의미한다. 마지막으로 $R$은 관측 잡음의 공분산 행렬에 해당된다.
칼만 필터는 고차원의 공분산 행렬을 처리하는 경우 음의 고유값이 발생하거나, 대칭성 및 양의 정부호성을 이탈하는 문제가 발생할 수 있다. 따라서 본 연구는 칼만필터의 일부 연산 과정을 개선하였다. Eq. (20)은 칼만 이득을 계산하는 방법이다. 그러나 본 연구에서는 Cholesky 분해를 활용한 Eq. (23)과 같은 형태로 칼만 이득을 계산하였다.
$$\begin{align}
S &= H\, P_{k}^{-} H^{T} + R \notag \\
S &= L^{T} L \quad \text{(where } S = \text{ upper triangular matrix)} \notag \\
K_{k} &= P_{k}^{-} H^{T}\, L^{-1}\,(L^{T})^{-1}
\end{align}$$
Cholesky 분해는 양의 정부호(positive-definite) 대칭 행렬에 대해 효율적으로 작동하며, 역행렬을 직접 계산하는 과정에서 발생할 수 있는 수치 불안정성을 크게 줄여준다 (Alexandros & David 2020). 특히, 공분산 행렬을 항상 삼각 행렬의 곱의 형태로 유지하기에 round-off error에 강인하여 계산과정에서 누적되는 수치오차를 줄여줄 뿐 만 아니라, 연산 과정에서 행렬이 항상 양의 정부호성과 대칭성을 유지하도록 한다는 장점이 있다 (Chandrasekar et al. 2001).
공분산 행렬을 갱신하는 과정 또한 Eq. (24)의 Joseph’s 안정화 형태 (Bucy & Joseph 1968)를 도입하여, Eq. (22)의 공분산 행렬 갱신 과정을 대체하였다.
$$P_{k}
=
( I – K_{k} H )
P_{k}^{-}
( I – K_{k} H )^{T}
+
K_{k} R K_{k}^{T}$$
이 또한, Eq. (23)의 Cholesky 분해와 같이 공분산 행렬의 양의 정부호성과 대칭성을 보장하여 상태공간의 차원 또는 조건수가 큰 환경에서 발생할 수 있는 수치적 불안정성을 해결할 수 있다.
Table 2는 자료처리 전략에 대해 상세히 나타낸 표이며, 각종 오차를 보정하는 과정에서 참조한 외부 산출물과, 데이터를 전처리하고 가중치를 부여한 방법을 나타낸다.
Table 2. Detailed Estimation Strategies for real-time clock estimation.
| Items | Strategies | |
|---|---|---|
| Data editing | Cut-off | Elevation angle (EL) < 7°; Signal to noise ratio (SNR) < 25 dB |
| Weights | 1.00 m and 0.03 m prior accuracy for code and phase observation respectively; Elevation-dependent weighting was applied for EL < 45°; SNR-dependent weighting was applied for signals with SNR < 32 dB | |
| Observation model | Observations | IF combination with undifferenced pseudo-range and carrier phase |
| Frequency and channel | C1W(C1C), C2W, L1W(L1C), L2W | |
| Differential code bias | CODE monthly P1C1 product | |
| Tidal effect | Solid Earth Tide (IERS Convention 2010) | |
| Earth Orientation Parameter (EOP) | IERS C04 | |
| Orbital motion of the Sun and Moon | JPL DE405 | |
| Receiver and satellite phase center offset and variation | IGS20_2335.atx | |
| Relativistic effect | Corrected | |
| Phase wind-up effect | Corrected (Wu et al. 1993) | |
| Clock Datum | Aligned to the mean of broadcast clock offset (Section 3.2) | |
| Orbit | Fixed to JPL Final SP3 | |
| Station coordinates | Fixed to IGS SINEX |
이번 장에서는, 추정 결과를 참값과 비교하고 그 특성을 분석한다. 본 연구에서는 30초 간격으로 제공되는 JPL 시계오프셋 최종 산출물을 참값으로 설정하였으며, 드리프트의 참값은 오프셋의 참값을 시간에 대해 중심 차분하여 획득하였다. 또한, 추정을 진행한 기간(2025/DOY005-007) 동안 PRN G01 및 G22는 불가용 상태였으므로 추정 대상에서 제외하였다. 4.1절에서는 반송파 위상 관측을 단독으로 사용하여 위성 시계 오프셋을 추정한 결과를, 4.2절에서는 반송파 위상 관측과 코드의사거리 관측을 결합하여 추정한 결과를 설명한다. 마지막으로 4.3절은 앞선 두 경우에서 위성 시계 드리프트를 추정한 결과를 설명한다.
우선, 반송파 위상 관측치만을 이용하여 위성 시계 오프셋을 추정하였다. 반송파 위상만 사용할 경우 모호정수의 영향으로 시스템의 자유도가 감소한다. 이러한 환경에서도 안정적으로 추정 과정을 진행하고 수렴시키기 위해서는 필터의 적절한 조정뿐만 아니라, 사이클 슬립에 대한 정확한 탐지 및 초기화 절차가 필요하다. 본 연구에서는 geometry-free combination (Hofmann-Wellenhof et al. 2008)과 Melbourne-Wübbena combination 관측치에 기반하여 사이클 슬립 발생 여부를 검출하고, 대응하였다 (Blewitt 1990). Fig. 6은 반송파 위상을 단독으로 사용하여 순방향 추정한 GPS 위성 시계 오프셋 오차의 시계열을 나타내며, Fig. 7은 각 블록에 대한 시계열 RMSE를 나타낸다. 본 연구에서 RMSE를 산출한 방식은 Eq. (25)와 같다.
$$\mathrm{RMSE}
=
\sqrt{
\sum_{i=1}^{n}
\frac{(\hat{y}_{i} – y_{i})^{2}}{n}
}$$
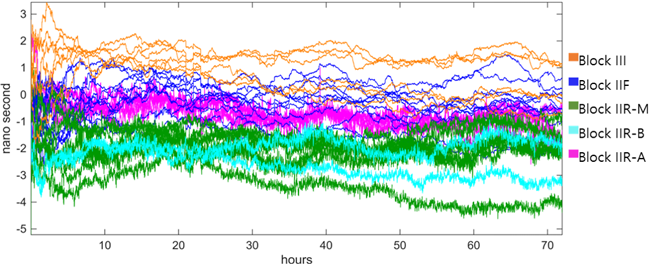
Fig. 6. A time series of the error between the estimated satellite clock offset and the true value during 2025/005–007, using carrier-phase only. Each color represents a GPS satellite block. Each line corresponds to an individual satellite.
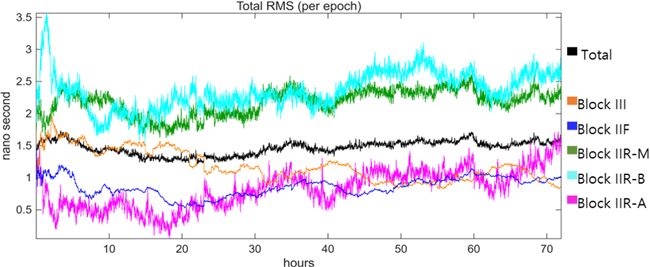
Fig. 7. Time series of the RMSE between the estimated satellite clock offset and the true value, using carrier-phase only. Each color and line represent a different GPS satellite block during 2025/005–007.
여기서 $n$은 데이터의 개수를 의미하며, $\hat{y}_{i}$는 추정한 값을 $y_i$는 이에 대응하는 참값을 뜻한다.
모든 위성에서 추정된 시계 오프셋은 참값 대비 ±3 ns 이내의 정확도를 보이며 블록별로 뚜렷한 클러스터링 패턴을 확인할 수 있다. Table 3에 제시된 블록별 통계 분석 결과는 이러한 패턴을 정량적으로 나타낸다. Table 3의 RMSE와 표준편차는 각 블록에 해당하는 위성 또는 전체 위성과 모든 에포크에 대해 산출하였다.
Table 3. Summary statistics of satellite clock offsets by GPS satellite block over all epochs in case of carrier phase observation.
| Block | # of sat. | RMSE (ns) | Standard deviation (ns) | Mean error (ns) |
|---|---|---|---|---|
| III IIF IIR-M IIR-B IIR-A | 6 (of 7) 11 7 2 4 (of 5) | 1.20 0.87 2.19 2.38 0.87 | 0.77 0.77 0.77 0.55 0.46 | 0.93 -0.40 -2.05 -2.31 -0.74 |
| Total | 30 (of 32) | 1.47 | 1.30 | -0.69 |
전체 위성에 대한 RMSE (1.47 ns) 대비 각 블록별 표준편차는 현저히 작은 값을 보인다. 각 블록의 RMSE 대비 표준편차 또한 작은 값을 보이며 블록 IIF의 표준편차 (0.77 ns)는 RMSE (0.87 ns)에 비해 약 90%, 블록 IIR-B의 표준편차 (0.55 ns)는 RMSE (2.38 ns)에 비해 약 23% 수준이다. 또한, 블록 III (0.93 ns), 블록 IIR-M (-2.05 ns), 블록 IIR-B (-2.31 ns) 등 다수 블록에서 평균 오차가 0에서 유의미하게 벗어나 있다. 이는 블록 내 위성들이 유사한 오차 특성을 공유하는 반면, 블록 간에는 큰 차이가 존재함을 의미한다.
코드 의사거리는 반송파 위상 관측치에 비해 약 100배에 달하는 높은 관측 잡음을 가진다. 따라서 후처리에서 정밀한 추정 결과를 도출할 때는 코드 의사거리를 제외해도 무방하다. 그러나 실시간 처리 환경에서는 반송파 위상 관측만으로 필터의 안정성을 확보하기 어렵다. 특히, 반송파 위상 관측치만 사용할 경우 자유도가 낮아 수렴 시간이 증가하며, 여러 에포크를 누적하여 후처리 하지 않으면 모호정수를 다른 변수와 엄밀히 분리하기 어렵다. 순차 필터에서는 적절한 초기값과 오차 특성 부여를 통해 이를 극복할 수 있지만, 시계의 불연속성 발생이나 사이클 슬립으로 인해 이상 관측치가 발생하면 필터 수렴에 부정적인 영향을 미쳐 안정성이 저해될 수 있다 (Mazher et al. 2016). 이러한 이유로, 실시간성을 중요시하는 선행 연구에서는 코드 의사거리를 반드시 반영하여 알고리즘을 설계하였으며, 본 연구 또한 최종적으로 코드 의사거리를 포함하여 결과를 도출하였다. Fig. 8은 반송파 위상과 코드의사거리를 결합하여 사용한 GPS 위성 시계 오프셋 추정 오차의 시계열을 나타내며, Fig. 9는 블록 별 RMSE에 대한 시계열을 나타낸다.
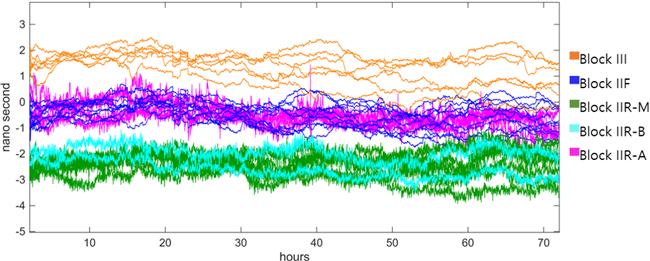
Fig. 8. A time series of the error between the estimated satellite clock offset and the true value during 2025/005–007, using both carrier-phase and pseudo range observations. Each color represents a GPS satellite block. Each line corresponds to an individual satellite.
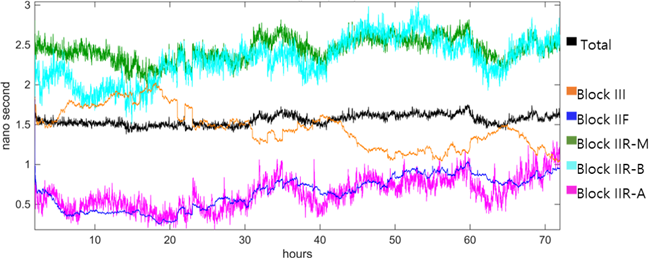
Fig. 9. Time series of the RMSE between the estimated satellite clock offset and the true value, using carrier-phase and pseudo range observations. Each color and line represent a different GPS satellite block during 2025/005–007.
반송파 위상만을 사용한 이전 결과와 마찬가지로 블록별 클러스터링 현상이 관찰되나, 그 분리 정도가 더욱 뚜렷하게 관찰된다. 블록 III는 약 1.5 ns 수준에서, Block IIF는 0 ns 부근에서, 블록 IIR-M과 IIR-B는 각각 -2.5 ns와 -2.0 ns 수준에서, Block IIR-A는 -0.5 ns 수준에서 명확히 구분되는 클러스터를 형성하였다. Table 4의 통계 분석 결과는 이러한 클러스터링의 심화를 정량적으로 보여준다.
Table 3과 비교하였을 때 전체 RMSE는 1.47 ns에서 1.56 ns로, 전체 표준편차는 1.30 ns에서 1.40 ns로 변화하였다. 블록별 표준편차는 모든 블록에서 감소하였으며, 감소폭은 블록 IIR-M에서 최대 42% 수준을, 블록 IIR-A에서 최소 13% 수준을 나타냈다. 이는 블록 별 클러스터링이 더욱 명확해짐을 의미한다. 평균 오차(mean error)의 변화 또한 블록 간 체계적 차이의 심화를 보여준다. 절댓값 기준으로 가장 큰 변화를 보인 블록 III은 0.93 ns에서 1.35 ns로 0.42 ns 변화하였으며, 가장 작은 변화를 보인 블록 IIR-B는 -2.31 ns에서 -2.28 ns로 0.03 ns 변화하였다. 이러한 평균 오차의 변화는 코드의사거리 추가 사용이 블록별 클러스터를 더욱 뚜렷하게 분리시키고 더욱 극명한 바이어스를 발생시킴을 의미한다.
Table 4. Summary statistics of satellite clock offsets by GPS satellite block over all epochs in case of carrier phase + pseudo range.
| Block | # of sat. | RMSE (ns) | Standard deviation (ns) | Mean error (ns) |
|---|---|---|---|---|
| III IIF IIR-M IIR-B IIR-A | 6 (of 7) 11 7 2 4 (of 5) | 1.48 0.68 2.41 2.30 0.66 | 0.60 0.48 0.45 0.48 0.40 | 1.35 -0.49 -2.40 -2.28 -0.53 |
| Total | 30 (of 32) | 1.56 | 1.40 | -0.69 |
위성 시계 드리프트 추정 결과는 관측치의 종류에 따른 차이는 크지 않았지만, 추정 정확도에 있어 블록에 따라 큰 차이를 보였다. Fig. 10은 반송파 위상만을 사용한 경우(좌측)와 반송파 위상 및 코드의사거리를 결합한 경우(우측)의 위성 시계 드리프트 추정 오차를 블록별로 나타낸 것이고, Table 5는 이를 수치적으로 분석한 결과이다.
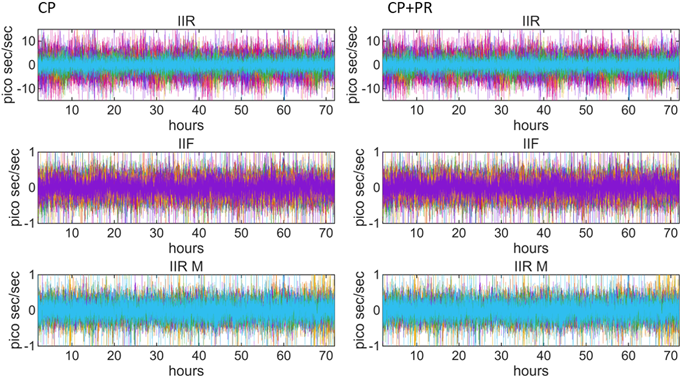
Fig. 10. Time series of satellite clock drift estimation errors for different GPS satellite. The left column shows the results obtained using carrier-phaseonly observations, while the right column presents the results obtained using both carrier-phase and pseudo range observations.
Table 5. Comparison of satellite clock drift RMSE across GPS satellite blocks and observation types.
| Block | # of sat. | RMSE (ps/s) | |
|---|---|---|---|
| Observation type | CP | CP+PR | |
| III IIF IIR-M IIR-B IIR-A | 6 (of 7) 11 7 2 4 (of 5) | 0.75 0.65 3.33 2.63 3.04 | 0.79 0.79 3.34 2.68 3.05 |
| Total | 30 (of 32) | 2.13 | 2.16 |
Fig. 10에서 확인할 수 있듯이 반송파 위상만을 단독으로 사용하였을 때와 코드의사거리와 함께 사용하였을 때의 드리프트 추정 양상은 유사함을 알 수 있다. Table 5를 참고하면, 반송파 위상을 단독으로 사용하였을 때 전체 RMSE 2.13 ps로 결합 관측(2.16 ps) 대비 약간 우수한 성능을 보였으나, 그 차이는 매우 작은 수준이다. 블록별로는 블록 III과 IIF가 각각 0.75 ps와 0.65 ps의 낮은 RMSE를 보인 반면, 블록 IIR 계열(IIR-M: 3.33 ps, IIR-B: 2.63 ps, IIR-A: 3.04 ps)은 높은 오차 수준을 나타냈다.
이러한 블록 IIR 계열의 낮은 정확도의 드리프트 추정 결과와, Figs. 6과 8에서 관찰되는 시계 오프셋 추정 시계열 오차의 높은 변동성은 Fig. 5의 Modified Allan Deviation 분석과 Fig. 4의 추세 제거 결과를 통해 설명할 수 있다. Fig. 5의 $\tau < 10^3\,\text{s}$ 범위에서, 블록 IIR 계열의 위성은 flicker phase noise가 우세하며 Modified Allan Deviation 값 또한 다른 블록에 비해 높다. 또한, Fig. 4를 참고하면 블록 IIR 계열은 블록 III에 비해 2차 추세 제거 후의 높은 잡음을 보이고 있다. 이는 블록 IIR계열의 시계에 선형 모델에서 벗어난 잡음이 비교적 많이 포함되어 있으며 이것이 추정 결과에 나타난 것으로 판단된다.
본 연구에서는 정밀 시각정보 생성을 위해 GPS 위성의 시계 오프셋과 드리프트를 실시간으로 추정하는 알고리즘 설계하였으며, 반송파 위상을 단독으로 사용한 결과와 반송파 위상과 코드의사거리를 결합하여 사용한 결과를 도출하였다. 또한, 추정 결과를 JPL 시계 오프셋 최종 산출물과 비교하여, 블록에 따른 평균 오차, 오차의 표준 편차, 평균 오차를 산출하고 분석하였다. 그 결과, 반송파 위상 단독 사용 시 추정 오차의 RMSE는 1.47 ns로 나타났으며, 반송파 위상과 코드 관측치를 결합했을 때는 1.56 ns의 RMSE를 보였다. 모든 위성에서 추정된 시계 오프셋은 참값 대비 ±3 ns 이내의 정확도를 유지하였다. 특히, 추정 오차는 GPS 위성 블록에 따라 뚜렷한 클러스터링 패턴을 형성했으며, 그 규모는 최대 2.5 ns에 이르는 바이어스로 나타났다. 코드 관측치를 결합했을 때, 오차의 표준편차가 모든 블록에서 감소하여 블록별 클러스터링이 더욱 명확해지는 현상을 확인하였다. 이는 코드 관측치에 포함된 체계적인 오차 성분이 블록별 바이어스를 더욱 두드러지게 만들었음을 의미한다.
본 연구 결과는 블록에 따른 바이어스가 코드 의사거리 관측치에 주로 존재하며, 반송파 위상 단독 사용 시에는 모호정수 초기화 과정에서 코드 의사거리가 사용되어 바이어스가 일부 유입되었을 가능성을 제시한다. 또한, 반송파 위상에도 유사한 바이어스가 포함되어 있으나 모호정수에 의해 희석되어 그 규모가 상대적으로 작게 나타났을 가능성도 있다.
실시간 추정된 시계 오프셋 정보를 이용해 센티미터급 측위 정확도를 달성하기 위해서는 RMSE를 1 ns 이하로 낮추어야 하므로, 이를 위하여 블록별 바이어스의 발생 원인을 규명하고 이를 보정해야 한다. 향후의 연구는 앞서 언급한 두 가지 가능성에 대해 검증하고, 위성의 하드웨어 특성으로부터 발생하는 오차에 대한 분석이 이루어져야 한다. 더 나아가, 사용하는 위성군과 신호대역을 확대하고 바이어스의 발생 유무와 블록 별 오차 특성을 분석하여야 한다. 또한, 정확도 향상과 더불어 추정기의 실시간 안정성에 대한 개선 또한 이루어져야 하며 수신기 및 위성 시계의 불연속 발생에 대응할 수 있는 알고리즘을 개발하고 적용하는 연구가 진행되어야 한다.
This research was supported by Korea Agency for Infrastructure Technology Advancement grant funded by the Ministry of Land, Infrastructure and Transport (RS2022- 00141819, Development of Advanced Technology for Absolute, Relative, and Continuous Complex Positioning to Acquire Ultra-precise Digital Land Information).
K.P. and H.R. proposed the research topic. Y.S. was responsible for the core research and algorithm development, with H.R. and K.P. providing guidance on the overall research direction, identifying relevant references, and specifying the required algorithmic functionalities. Y.K. directly contributed to the algorithm development and validation.
The authors declare no conflict of interest.
Alexandros, E. & David, P. 2020, Quantitative Verification of Numerical Stability for Kalman Filters, University of Birmingham, UK.
Anthony, T. 2022, NAVSTAR GPS Space Segment/Navigation User Segment Interfaces, U.S. Space Force, IRN-IS-200M-001.
Blewitt, G. 1990, An automatic editing algorithm for GPS data, Geophys. Res. Lett., 17, 199-202. https://doi.org/10.1029/GL017i003p00199
Boehm, J., Niell, A., Tregoning, P., & Schuh, H. 2006, Global mapping function (GMF): A new empirical mapping function based on numerical weather model data, Geophys. Res. Lett., 33, L07304. https://doi.org/10.1029/2005GL025546
Bucy, S. & Joseph, D. 1968, Filtering for Stochastic Processes with Applications to Guidance, Pure and Applied Mathematics, vol.23, Interscience Publishers (New York: AMS Chelsea Publishing).
Chandrasekar, J., Michels, J. H., & Hero, A. O. 2001, Cholesky-Based Reduced-Rank Square-Root Kalman Filter, Department of Electrical Engineering and Computer Science, University of Michigan.
Chen, L., Li, M., Zhao, Y., Hu, Z., Zheng, F., et al. 2021, Multi-GNSS real-time precise clock estimation considering the correction of inter-satellite code biases, GPS Solut., 25, 32. https://doi.org/10.1007/s10291-020-01065-z
European Space Agency Navipedia, combination of GNSS measurements [Internet], cited 2025 Sep 5, available from: https://gssc.esa.int/navipedia/index.php/Combination_of_GNSS_Measurements
Fernández, E., Calero, D., & Parés, M. E. 2017, CSAC characterization and its impact on GNSS clock augmentation performance, Sensors, 17, 370. https://doi.org/10.3390/s17020370
Grewal, M. S. & Andrews, A. P. 2015, Kalman filtering: Theory and practice with MATLAB, 4th ed. (Hoboken, NJ: John Wiley & Sons).
Han, S.-C. & Jekeli, C. 1998, GPS satellite clock estimation every 30 seconds and application to accurate absolute positioning, Ohio State University Research Foundation Technical Report, August 1998.
Hauschild, A. 2011, Precise GNSS clock-estimation for real-time navigation and precise point positioning, DLR Deutsches Zentrum für Luft- und Raumfahrt e.V. – Forschungsberichte, 1-145.
Hofmann-Wellenhof, B., Lichtenegger, H. & Wasle, E. 2008, GNSS – Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More (Vienna: Springer).
Huang, G., Xie, W., Fu, W., Li, P., Wang, H., et al. 2021, BDS Real-time Satellite Clock Offsets Estimation with Three Different Datum Constraints, JGPS, 17, 34-47. https://doi.org/10.5081/jgps.13.1.34
IEEE 1998, IEEE standard specification format guide and test procedure for single-axis interferometric fiber optic gyros, IEEE Std 952-1997, Institute of Electrical and Electronics Engineers.
International GNSS Service, orbit and clock product [Internet], cited 2025 Jul 15, available from: https://igs.org/products/#orbits_clocks
International GNSS Service, network [Internet], cited 2025 Jul 15, available from: https://network.igs.org/
Kim, Y.-G., Rim, H.-J., Ha, J., Sung, H.-J., & Park, K.-D. 2024, Study on Precise Orbit Determination of GPS Satellites Using Batch Filter, in Proceedings of the 2024 IPNT Conference, Jeju, Korea, 6-8 November 2024, pp.55-58. https://ipnt.or.kr/2024proc/160
Lee, H.-C. & Park, K.-D. 2020, Development of code-PPP based on multi-GNSS using compact SSR of QZSS-CLAS, J. Korean Soc. Surv. Geod. Photogramm. Cartogr., 38, 521-531. https://doi.org/10.7848/ksgpc.2020.38.6.521
Liu, T., Zhang, B., Yuan, Y., Zha, J., & Zhao, C. 2019, An efficient undifferenced method for estimating multi-GNSS high-rate clock corrections with data streams in real time, J. Geod., 93, 1435-1456. https://doi.org/10.1007/s00190-019-01255-9
Maciuk, K. & Lewińska, P. 2019, High-Rate Monitoring of Satellite Clocks Using Two Methods of Averaging Time, Remote Sens., 11, 2754. https://doi.org/10.3390/rs11232754
Mazher, K., Tahir, M. & Ali, K. 2016, GNSS pseudorange smoothing: linear vs non-linear filtering paradigm, in Proc. IEEE Aerospace Conf., Big Sky, MT, March 2016, pp.1-10. Available from: https://web.lums.edu.pk/~spnav/khurram/Aero.pdf
Rovira-Garcia, A., Juan, J. M., Sanz, J., González-Casado, G., Ventura-Traveset, J., et al. 2021, A multi-frequency method to improve the long-term estimation of GNSS clock corrections and phase biases, NAVIGATION, 68, 815-828. https://doi.org/10.1002/navi.453
Saastamoinen, J. 1972, Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites, in The Use of Artificial Satellites for Geodesy, Geophysical Monograph Series, American Geophysical Union, pp.247-251. https://doi.org/10.1029/GM015p0247
Shin, S.-Y., Han, J.-M., & Park, K.-D. 2024, Analysis of the differences between CLAS L6 message from the QZSS public archives and CLAS correction messages received by actual GNSS receivers, J. Positioning Navig. Timing, 13, 485-495. https://doi.org/10.11003/JPNT.2024.13.4.485
Swift, E. R. 1987, Mathematical description of the GPS multi satellite filter/smoother, NSWC TR 87-187, Naval Surface Warfare Center, Dahlgren, VA.
Wu, J. T., Wu, S. C., Hajj, G., Bertiger, W. I., & Lichten, S. M. 1993, Effects of antenna orientation on GPS carrier phase, Manuscr. Geod. 18, 91-98. https://doi.org/10.1007/BF03655303
Zhang, X., Li, X., & Guo, F. 2011, Satellite clock estimation at 1 Hz for realtime kinematic PPP applications, GPS Solut., 15, 315-324. https://doi.org/10.1007/s10291-010-0191-7
Zuo, X., Jiang, X., Li, P., Wang, J., Ge, M., et al. 2021, A square root information filter for multi-GNSS real-time precise clock estimation, Satellite Navig., 2, 28. https://doi.org/10.1186/s43020-021-00060-0