Time and Frequency Group, Strategic Technology Research Institute, Korea Research Institute of Standards and Science (KRISS), Daejeon 34113, Korea
Citation: Lee, J., Heo, Y.-J., Oh, J.-I., Rhee, J. H., Choi G. W., et al. 2025, Instability Analysis of TWSTFT and GPS Time Comparison using a Double Difference Three-Cornered Hat, Journal of Positioning, Navigation, and Timing, 14, 221-229.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 221-229. https://doi.org/10.11003/JPNT.2025.14.3.221
Received on Aug 08, 2025, Revised on Aug 22, 2025, Accepted on Aug 25, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Precise time synchronization is crucial for modern infrastructure but objectively evaluating the intrinsic performance of technologies such as Global Positioning System (GPS) Precise Point Positioning (PPP), Integer Precise Point Positioning (IPPP), P3, and Two-Way Satellite Time and Frequency Transfer (TWSTFT) is challenging due to the influence of local time source stability. This paper proposes a Double Difference-based Three-Cornered Hat (TCH) method to overcome this limitation. By applying this technique to analyze TWSTFT and GPS links between Korea Research Institute of Standards and Science (KRISS) and Physikalisch-Technische Bundesanstalt (PTB), we confirmed a stability of mid 10−17 for averaging times over 2×106 seconds, consistent with similar research by the National Institute of Standards and Technology (NIST). Our findings provide an important standard for evaluating high-precision links and offers a practical foundation for technology selection and system design in fields such as national time standards and defense.
TWSTFT, GPS, instabilities analysis, double difference three-cornered hat, TDEV, MDEV
현대 사회의 정밀 시각 동기 기술은 통신, 금융, 항법, 전력망, 과학 연구 등 다양한 분야의 핵심 인프라 운영에 필수적인 요소이며, 충분하지 않은 성능으로 시각 동기가 이루어질 경우 전체 시스템의 안정성과 신뢰성이 심각하게 저하될 수 있다. 예를 들어, 금융 거래 시스템에서는 거래 요청과 처리 시각이 ms 이하로 동기되지 않으면 거래에 오류가 발생할 수 있으며, 위성항법시스템(Global Navigation Satellite System, GNSS)에서는 시각 동기 오차가 의사거리 측정 오차로 직접 전이되어 수 ns 수준의 시각 동기가 요구된다.
이러한 요구를 충족하기 위해 다양한 시각 동기 기술을 활용할 수 있다. 대표적으로 Global Positioning System (GPS) 기반의 Precise Point Positioning (PPP), Integer Precise Point Positioning (IPPP), P3 코드 조합 방식과 위성 기반 양방향 시각 및 주파수 전송(Two-Way Satellite Time and Frequency Transfer, TWSTFT) 기술이 있다. 각 기술은 전파 형식, 관측 방식, 보정 처리 방식이 상이하여 고유한 성능 특성을 가지며, 실제 적용 환경과 목적에 따라 장단점이 다르게 나타난다.
이러한 기술들을 활용하여 수행한 시각 비교 결과는 기준지 및 원격지의 시각원의 안정도와 시각 비교 기술 자체의 성능이 반영되어 있다. 즉, 측정 결과에는 시각 비교 기술 자체의 성능뿐만 아니라 시각원의 성능이 포함되어 있어, 단순 비교만으로는 시각 동기 기술 간의 본질적인 성능 비교를 수행하기 어렵다. 이러한 문제를 해결하기 위해 본 연구에서는 이중 차분(double difference, DD) 기반 Three-Cornered Hat (TCH) 기법을 적용한다. 이 방법은 세 개 이상의 독립적인 시각 비교 결과를 조합하여 시각원의 영향을 제거하고, 각 시각 비교 기술 고유의 성능을 분리하여 정량화 할 수 있다 (Parker et al. 2022).
본 논문에서는 먼저 2장에서 GPS PPP, GPS IPPP, GPS P3, TWSTFT의 원리와 개념을 설명하고, 3장에서는 이중 차분 TCH 기법의 수학적 원리와 적용 절차를 기술한다. 4장에서는 실제 측정 데이터를 이용하여 각 기술의 성능을 비교 분석한 결과를 제시하며, 마지막으로 5장에서는 결론과 함께 활용 방안을 제시한다.
원거리에 위치한 두 지점의 시각을 정밀하게 비교하기 위해 다양한 기술이 개발되었으며, 그중 위성 시각비교 기술은 위성에 탑재된 시계 또는 중계기를 매개체로 하여 지상의 두 시계 간의 시간 차이를 측정하는 원리이다. 본 장에서는 대표적인 기술인 TWSTFT 방식과 GPS 기반 시각비교 기술에 대해 설명한다.
TWSTFT는 시각비교를 수행하려는 두 지점의 기준국에서 동시에 동일한 통신위성을 향해 시각 신호를 송신하고, 동시에 상대방 기준국에서 송신한 신호를 수신하는 방식이다. 각 기준국은 자신이 송신한 신호가 위성을 거쳐 되돌아오는 시간과 상대방 관측소에서 보낸 신호가 도착하는 시간을 정밀하게 측정한다. 각 기준국에서는 원자시계로부터 발생한 신호에 Binary Phase-Shift Keying (BPSK) 및 Pseudo-Random Noise (PRN) 코드 변조를 수행하며, 위성을 통해 이 RF 신호를 각 기준국 간에 송수신하여 시각 비교를 수행한다. 위성을 통한 신호 송수신 시 전리층, 대류층, 지구 자전 효과 등 다양한 오차 요인들이 존재하지만, 각 기준국에서 측정한 측정치 간 차분을 통해 이들 중 상당 부분이 제거된다. 이러한 특성 덕분에 TWSTFT는 현재 운용되는 시각비교 기술 중 가장 높은 정확도(수 나노초 이하)를 제공하는 한 가지 방법이며, 전 세계 국가표준기관 간의 국제 시각비교 및 UTC 생성에 핵심적인 역할을 수행하고 있다 (ITU-R TF.1153 2015, Cheng et al. 2022).
GNSS 기반 시각비교는 국제표준시(UTC) 구축, 국가 표준시 운영 및 국제 원자시(International Atomic Time, TAI) 조정 등에 적용되고 있다 (BIPM 2020). GNSS 기반 시각비교는 대표적으로 P3 코드 결합법, PPP, 그리고 integer ambiguity resolution을 포함한 IPPP 기법이 있다 (Jiang et al. 2005). P3 시각비교기법은 GPS 위성의 두 주요 주파수 대역(L1, L2)에서 수신되는 P1 및 P2코드 측정치를 선형 조합하여 시각비교 정확도를 저해하는 가장 큰 오차 요소인 전리층 지연을 효과적으로 제거(ionospheric free)하는 고전적이면서도 안정적인 방법으로, 국제 표준규격 Common Generic GNSS Time and Frequency (CGGTTS)으로 채택되어 국가 간 시각비교 수단으로 널리 활용되고 있다 (Defraigne & Petit 2015). 또한, 국제도량형국(Bureau International des Poids et Mesures, BIPM)은 2009년 9월부터 TAI 계산을 위해 GNSS를 활용한 PPP 기법을 적용하고 있다 (Petit & Jiang 2008). PPP는 International GNSS Service (IGS) 등에서 제공하는 고정밀 위성 궤도 및 시계 보정 정보를 활용하여 GNSS 관측 모델에 포함된 모든 오차 요인을 개별적으로 정밀하게 모델링하고 제거한다. 수신기 위치, 수신기 시계 오차, 대류층 지연, 반송파 위상 미지정수 등을 미지수(unknown parameter)로 설정하고, 칼만 필터(Kalman filter)와 같은 추정 기법을 통해 해를 구한다. 일반적으로 반송파 위상 미지정수(carrier phase ambiguity)를 실수(real number)로 추정하며, 이를 ‘PPP 플롯(Float) 해’라고 부른다. 여기서 추정된 ‘수신기 시계 오차’ 항이 바로 GNSS 기준 시각 대비 수신기 시계의 정밀한 오프셋 값이 된다. 시각비교기법에서는 GNSS 수신기마다 독립적으로 산출한 PPP 해로부터 구한 ‘수신기 시계 오프셋’ 차이를 통해 지점 간 정밀한 시각비교가 이루어진다. 하지만 반송파 위상 미지정수를 실수로 추정하기 때문에, 안정적인 해를 얻기까지 일정 수준 이상의 수렴 시간이 요구되고, 반송파 위상 측정치 사용을 위한 Float형 미지정수 추정 시 적용된 코드 측정치 사용으로 주파수 안정도의 한계를 갖는다. PPP 기법의 한계인 긴 수렴 시간을 극복하고 정확도를 향상시키기 위한 방법으로 실수로 추정하던 반송파 위상 미지정수를 본래의 값인 정수(integer)로 고정하는 IPPP 기법이 있다. 미지정수 결정이 성공하면 매우 빠르고 정확한 해를 얻을 수 있어, 나노초 이하 수준의 시각비교가 가능하다.
TCH은 시계 간 성능 비교 및 이를 활용한 각 시각원의 안정도를 평가하는 대표적인 알고리즘이다. 3개의 독립적이고 유사한 안정도를 가지는 서로 다른 시각원이 존재하는 경우를 가정하며, 서로 다른 3개의 시각원 위상이 $x_a(t),\; x_b(t),\; x_c(t)$인 경우, 각 시각 원 간의 시각 차 측정치 $x_a(t) – x_b(t),\;
x_b(t) – x_c(t),\; x_c(t) – x_a(t)$ 간 관계를 Eq. (1)과 같이 표현할 수 있다.
$$\begin{align}
x_{a}(t) – x_{b}(t)
&= -[ x_{c}(t) – x_{a}(t) ] – [ x_{b}(t) – x_{c}(t) ] \notag \\[4pt]
x_{b}(t) – x_{c}(t)
&= -[ x_{a}(t) – x_{b}(t) ] – [ x_{c}(t) – x_{a}(t) ] \notag \\[4pt]
x_{c}(t) – x_{a}(t)
&= -[ x_{b}(t) – x_{c}(t) ] – [ x_{a}(t) – x_{b}(t) ]
\end{align}$$
Eq. (1)의 관계를 활용하여, 각 시각원의 안정도를 $\sigma_a$, $\sigma_b$, $\sigma_c$로 정의하고, 각 시각 원 간의 시각 차 측정치 $x_a(t) – x_b(t),\; x_b(t) – x_c(t),\; x_c(t) – x_a(t)$에 대한 안정도를 $\sigma_{a,b}$, $\sigma_{b,c}$, $\sigma_{c,a}$라고 한다면, 2개의 시각원 간 시각 차 측정치 안정도와 각 시각원의 안정도의 관계는 Eq. (2)와 같은 관계를 갖는다.
$$\begin{align}
\sigma_{a,b}^{2} &= \sigma_{a}^{2} + \sigma_{b}^{2} \notag \\[4pt]
\sigma_{b,c}^{2} &= \sigma_{b}^{2} + \sigma_{c}^{2} \notag \\[4pt]
\sigma_{c,a}^{2} &= \sigma_{c}^{2} + \sigma_{a}^{2}
\end{align}$$
Eq. (2)로부터 개별 시각원의 안정도를 Eq. (3)과 같이 도출할 수 있다.
$$\begin{align}
\sigma_{a} &= \sqrt{\frac{1}{2}\left(\sigma_{a,b}^{2} + \sigma_{c,a}^{2} – \sigma_{b,c}^{2}\right)} \notag \\[6pt]
\sigma_{b} &= \sqrt{\frac{1}{2}\left(\sigma_{a,b}^{2} + \sigma_{b,c}^{2} – \sigma_{c,a}^{2}\right)} \notag \\[6pt]
\sigma_{c} &= \sqrt{\frac{1}{2}\left(\sigma_{c,a}^{2} + \sigma_{b,c}^{2} – \sigma_{a,b}^{2}\right)}
\end{align}
$$
단 Eqs. (2, 3)과 같은 관계를 갖기 위해서는 각 시각 원의 위상 간에 상관성이 없어야 하며, 각 시각원 간의 상관성이 존재할 경우, TCH 기반 안정도 평가 결과가 음수 값을 갖는 등의 정확한 추정이 어려운 한계를 갖는다. TCH 알고리즘의 시각 차 측정치들과 시계 간 관계는 Fig. 1과 같다 (Vernotte et al. 2004, Sjoberg et al. 2021).
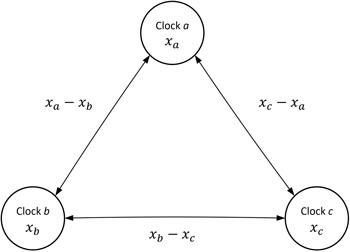
Fig. 1. Basic principle of the three-cornered hat method.
TCH 분석방법은 시계 간 성능을 평가하기 위해 활용되는 대표적인 알고리즘이나, 다양한 대상을 평가하는데 활용할 수 있으며, 대기환경 데이터, 원격탐사 데이터, 수자원 및 에너지 분야 데이터들 간의 품질 및 성능 평가에 활용되고 있다 (He et al. 2020, Sjoberg et al. 2021, Fang & Ma 2025).
3.1절에서 소개한 TCH 분석 방법을 활용하여, 2개의 동일한 시각원을 대상으로 구축되어 있는 시각비교 시스템 간 성능 분석을 수행할 수 있다. 미국 표준기관인 National Institute of Standards and Technology (NIST)에서 2019년 11월부터 2021년 5월까지 수집한 데이터를 활용하여 2개의 TWSTFT 기반 시각비교 시스템과 GPS 기반 시각비교 시스템의 시각비교 성능평가를 수행한바 있다. NIST의 연구에서는 미국내에 위치한 두 기준 시각원인 UTC(NIST)와 UTC(USNO) 간 구축된 TWSTFT Direct Two-Way (DTW), TWSTFT Indirect Two-Way (ITW), GPS 반송파 기반 IPPP 시각비교 링크를 분석하였다. 미국 연구 사례에서는 TWSTFT DTW 링크로 코드율(code rate) 1 Mchip/s의 Ku 대역 신호를 활용하였으며, TWSTFT ITW 링크로는 EU-USA 간 국제시각비교 채널 중 독일의 Physikalisch-Technische Bundesanstalt (PTB)를 매개로 UTC(NIST)-UTC(PTB), UTC(PTB)-UTC(USNO) 간 시각 차 측정치를 차분하여 활용하였고, 해당 링크는 코드율 2.5 Mchip/s의 Ku 대역 신호가 사용되었다. 또한 시각비교용 GPS 수신기로는 Novatel GPS 수신기를 활용하였다. NIST의 주파수 안정도 평가 결과 링크 별 소폭의 차이는 있으나, 평균시간 20일에 대해 1×10-16 수준의 Modified Allan Deviation (MDEV)과 총 분석구간 85일에 대해서 mid 10-17 수준의 MDEV을 도출하였다 (Parker et al. 2022).
본 논문에서는 UTC(KRIS)와 UTC(PTB) 간 시각비교 링크들을 대상으로 UTC(KRIS)와 UTC(PTB) 간 시각비교 링크의 측정치에 대해 이중 차분 TCH 분석기법을 활용하여 평가하였다. TWSTFT의 경우, 러시아의 Express-80 위성을 활용하여 코드율 2.5 Mchip/s Ku 대역 신호로 운용되고 있는 EU-Asia 링크 중 UTC(KRIS)와 UTC(PTB) 간 시각비교 채널을 활용하였다. GPS 시각비교 링크의 경우, 한국표준과학연구원과 PTB에서 각각 UTC 생성에 기여하고 있는 국제 시각비교용 GNSS 수신기를 활용하였으며, GPS IPPP, PPP, P3 기반 시각비교 링크를 성능 평가 대상으로 선정하였다.
소개한 UTC(KRIS)와 UTC(PTB) 간의 시각비교 링크들의 관계는 Fig. 2와 같다. Fig. 2에서 UTC(PTB)와 UTC(KRIS)의 위상이 각각 $x_{UTC(PTB)}$와 $x_{UTC(KRIS)}$이고, 각 시각비교 기술을 n으로 정의 할 경우, 시각비교 링크를 통해 두 시각원의 시각차를 측정할 수 있으며 측정된 시각차는 Eq. (4)와 같이 표현할 수 있다.
$$D_{KRIS-PTB}^{\,n} = x_{UTC(KRIS)} – x_{UTC(PTB)} + e_{KRIS-PTB}^{\,n}$$
여기서 $e_{KRIS-PTB}^n$는 시각비교 기술 $n$이 가지는 두 시각원의 시각 차 성분을 제외한 잔차이며, Eq. (4)에서 서로 다른 시각비교 기술 $n$과 $m$에 대해 한번 더 차분을 수행하면 Eq. (5)와 같이 표현할 수 있다.
$$D\, D_{KRIS-PTB}^{\,n,m} = D_{KRIS-PTB}^{\,n} – D_{KRIS-PTB}^{\,m}$$
Eq. (5)에 Eq. (4)의 관계를 적용하여 UTC(PTB)와 UTC(KRIS)의 위상차를 배제하고 시각비교 기술의 잔차 간의 관계를 정의 할 수 있으며, 이는 Eq. (6)과 같이 표현 가능하다.
$$\begin{align}
D\,D_{KRIS\!-\!PTB}^{\,n,m}
&= \bigl[ x_{UTC(KRIS)} – x_{UTC(PTB)} + e_{KRIS\!-\!PTB}^{\,n} \bigr]
– \bigl[ x_{UTC(KRIS)} – x_{UTC(PTB)} + e_{KRIS\!-\!PTB}^{\,m} \bigr] \notag \\[6pt]
&= e_{KRIS\!-\!PTB}^{\,n} – e_{KRIS\!-\!PTB}^{\,m}
\end{align}
$$
Eq. (6)과 같이 이중 차분한 결과를 활용하여, 3.1절에서 소개한 TCH을 수행할 수 있으며, 서로 다른 $DD_{KRIS-PTB}^{n,m}$ 간 TCH 조합을 통하여 시각비교 링크 간 성능평가를 수행할 수 있다. 본 논문에서는 TWSTFT(TW), GPS IPPP, PPP, P3 시각비교 기술을 대상으로 이중 차분 TCH 성능평가를 수행하였으며, $n$ 및 $m$이 상기 서술한 4가지 시각비교 기술일 경우, 모든 경우의 수에 대해 Eq. (7)과 같이 표현 가능하다. 이중 차분 측정치와 시각비교 기술 간의 관계는 Fig. 3과 같다.
$$\begin{bmatrix}
D D_{\text{KRIS-PTB}}^{TW,IPPP} \\
D D_{\text{KRIS-PTB}}^{TW,PPP} \\
D D_{\text{KRIS-PTB}}^{IPPP,PPP} \\
D D_{\text{KRIS-PTB}}^{TW,P3} \\
D D_{\text{KRIS-PTB}}^{IPPP,P3} \\
D D_{\text{KRIS-PTB}}^{PPP,P3}
\end{bmatrix}
=
\begin{bmatrix}
1 & -1 & & \\
1 & & -1& \\
& 1 & -1& \\
1 & & & -1\\
& 1 & & -1\\
& & 1 & -1
\end{bmatrix}
\begin{bmatrix}
D_{\text{KRIS-PTB}}^{TW} \\
D_{\text{KRIS-PTB}}^{IPPP} \\
D_{\text{KRIS-PTB}}^{PPP} \\
D_{\text{KRIS-PTB}}^{P3}
\end{bmatrix}$$
Eq. (7)에서 표현된 6가지 이중 차분 측정치를 활용하여 모든 경우에 대하여 TCH을 수행한다면 총 4가지 경우를 정의할 수 있으나, GPS IPPP, PPP, P3 시각비교 링크 간에는 높은 상관성을 갖으며, 모든 경우가 GPS 시각비교 기술 기반인 경우, Time Deviation (TDEV) 및 Modified Allan Deviation (MDEV) 이 많은 평균시간 구간에 대하여 음수로 평가되어 성능평가 경우의 수에서 제외하였다.
이에 따라 TWSTFT 링크 평가 시 3가지 경우, GPS IPPP, PPP, P3 평가 시 각각 2가지 경우의 수를 얻을 수 있다. TWSTFT, GPS IPPP, PPP 조합에 대해 Case 1, TWSTFT, GPS IPPP, P3 조합에 대해 Case 2, TWSTFT, GPS PPP, P3 조합에 대해 Case 3으로 정의하고, 시각비교 기술 $n$에 대해 각 Case를 $k$로 정의하여, 시각비교 링크의 안정도를 $\sigma_{n(k)}$로 시각비교 기술 $n$ 및 $m$에 대한 이중 차분 측정치의 안정도를 $\sigma_{n,m}$으로 표현한다면, Eq. (3)의 관계로부터 이중 차분 TCH을 통해 얻을 수 있는 모든 평가 결과를 Eq. (8)과 같이 도출할 수 있다.
$$\begin{bmatrix}
\sigma_{TW(1)}^{2} \\
\sigma_{TW(2)}^{2} \\
\sigma_{TW(3)}^{2} \\
\sigma_{IPPP(1)}^{2} \\
\sigma_{IPPP(2)}^{2} \\
\sigma_{PPP(1)}^{2} \\
\sigma_{PPP(3)}^{2} \\
\sigma_{P3(2)}^{2} \\
\sigma_{P3(3)}^{2}
\end{bmatrix}
=
\frac{1}{2}
\begin{bmatrix}
1 & 1 & -1 & & & \\
1 & & & 1 & -1 & \\
& 1 & & 1 & & -1\\
1 & -1& 1 & & & \\
1 & & & -1& 1 & \\
-1& 1 & 1 & & & \\
& 1 & & -1& & 1 \\
-1& & & 1 & 1 & \\
& -1& & 1 & & 1
\end{bmatrix}
\begin{bmatrix}
\sigma_{TW,IPPP}^{2} \\
\sigma_{TW,PPP}^{2} \\
\sigma_{PPP,IPPP}^{2} \\
\sigma_{TW,P3}^{2} \\
\sigma_{IPPP,P3}^{2} \\
\sigma_{PPP,P3}^{2}
\end{bmatrix}$$

Fig. 2. Time transfer links between UTC(KRIS) and UTC(PTB).
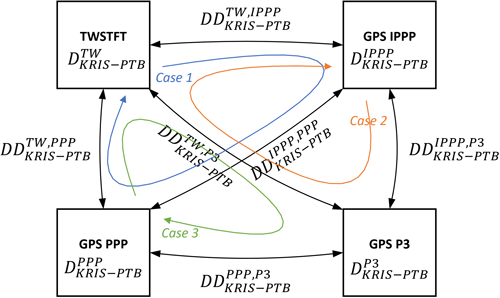
Fig. 3. Time transfer links and double difference measurements between UTC(KRIS) and UTC(PTB).
본 논문에서는 3.2절에서 서술한 이중 차분 TCH 기반 시각비교 링크 별 성능 분석을 위해, BIPM 서버의 국제시각비교 측정치 데이터를 활용하였으며, 시각비교 측정치 간 급격한 위상천이가 없는 비교적 정상상태로 운영된 구간을 대상 분석 구간으로 선정하였다. 분석 대상으로 선정한 구간은 UTC 2021년 12월 01일(Modified Julian Date, MJD 59549)에서 UTC 2022년 6월 7일(MJD 59737)로 188일이며, TDEV 및 MDEV 평가 시 평균시간 약 3×106초까지 분석이 가능하도록 구성하였다. TDEV은 시각 오차의 편차로 시계 혹은 시각비교 시스템의 단기 및 중기 안정도를 평가할 수 있으며, 특정 관측 평균시간(τ)동안 시계 오차가 얼마나 크게 변동하는지를 나타내는 지표이다. MDEV은 주파수 안정도를 평가하는 대표적인 방법으로, MDEV를 활용하여 관측 평균시간에 따른 주파수 안정도를 확인할 수 있으며, 다양한 잡음 특성들과 주파수 drift 성분을 평가할 수 있다. 논문에서는 TDEV과 MDEV를 활용하여, 각 시각비교 링크의 시각 편차와 주파수 안정도를 분석하였다.
서로 다른 시각비교 시스템을 기반으로 한 측정치를 활용함에 따라, 몇 가지 측정치 전처리를 수행하였다. BIPM에서 제공한 데이터의 이전 월말 및 다음 월초에 중복된 MJD를 가지는 구간의 offset을 다음 월초 데이터를 기준으로 보정하였고, 이중 차분 데이터가 동일한 time tag를 가지도록 구성하기 위해 상대적으로 raw 데이터 측정주기가 긴 TWSTFT 시각비교 데이터를 기준으로, GPS IPPP, PPP, P3 데이터를 보간하여 동일 time tag를 갖는 데이터셋을 도출하였다. 또한 운용 과정에서 발생하는 큰 수치의 outliner를 제거하여, 안정도 분석 과정에서 낮은 평균시간에 대해 발생할 수 있는 spurious를 방지하였다. 본 논문에서 활용한 전처리 과정을 거친 링크 별 UTC(KRIS)와 UTC(PTB) 간 시각비교 측정치는 Fig. 4와 같다.
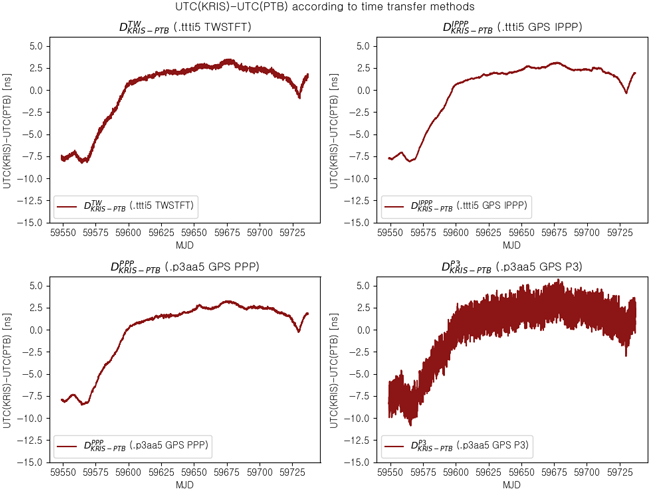
Fig. 4. BIPM TWSTFT, GPS IPPP, PPP, P3 time comparison measurements from *p3aa5, *t3ia5, *.ttti5 files between UTC(KRIS) and UTC(PTB).
Fig. 4에서 확인할 수 있듯이, 시각비교 링크에 따라 서로 다른 단기적인 시각비교 오차 수준을 갖으나, 장기적인 위상변화 추이는 유사함을 확인할 수 있다. 이는 UTC(KRIS)와 UTC(PTB) 간 발생하는 시각 원 간 위상 차 변화로 인한 것으로, 시각 원 간 위상 차를 배제하기 위해 Eq. 7과 같이 한번 더 차분하여 Fig. 5와 같은 이중 차분 측정치를 산출하였다.
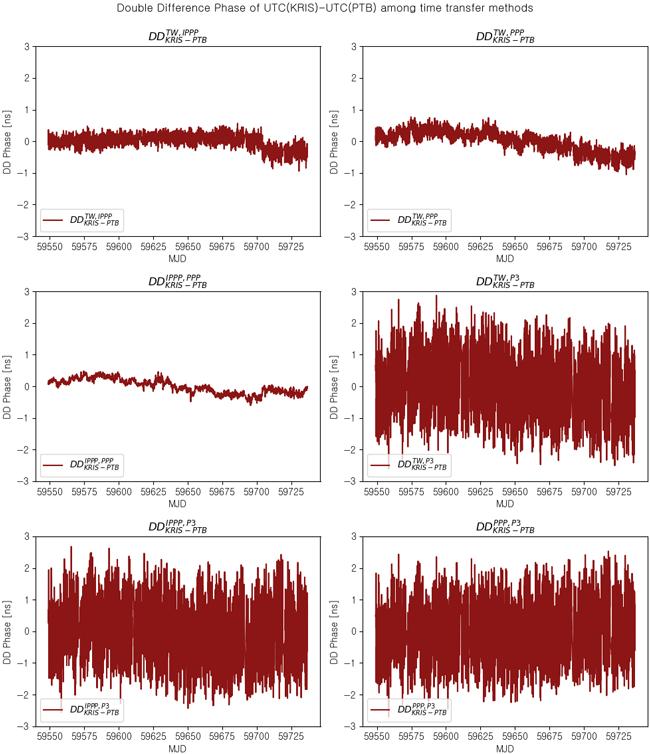
Fig. 5. Double difference time comparison measurements among TWSTFT, GPS IPPP, PPP and P3 of UTC(KRIS)-UTC(PTB) after pre-processing.
Fig. 5와 같이 각 시각비교 링크 간의 특성에 의해, 차분 시 다른 오차 수준을 갖으며, GPS P3가 포함된 이중 차분 측정치의 경우 P3가 가지는 상대적으로 큰 오차 수준에 의해 약 4 ns 정도의 편차가 산출됨을 확인할 수 있다. TWSTFT와 GPS IPPP, PPP 간에는 약 1 ns 수준, 가장 유사한 오차 특성을 갖는 GPS IPPP와 PPP 간에는 약 0.5 ns 수준의 편차가 산출되었다. Eq. 8을 적용하고, 이중 차분 측정치의 시각 편이를 분석하기위해 TDEV을 산출하였으며, 산출 결과는 Fig. 6과 같다.
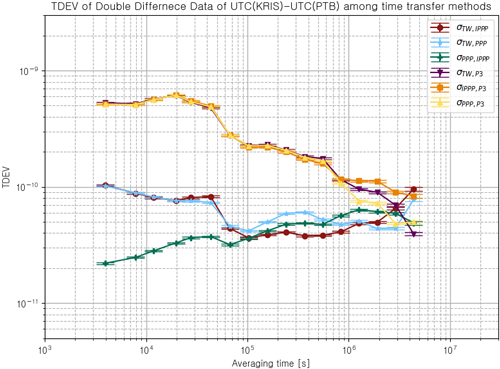
Fig. 6. Time deviation (TDEV) of UTC(KRIS)-UTC(PTB) according to double difference time comparison data.
Fig. 6과 같이, 약 4×103초의 상대적으로 단기(short-term) TDEV의 경우, GPS P3가 포함된 $\sigma_{TW,P3}$, $\sigma_{IPPP,P3}$, $\sigma_{PPP,P3}$가 약 5×10-10, $\sigma_{TW,IPPP}$, $\sigma_{TW,PPP}$가 약 1×10-10, $\sigma_{PPP,IPPP}$가 약 2×10-11으로 서로 다른 시각 편이 수준 차이를 보였으나, 1×106초의 상대적으로 장기(long-term) TDEV은 3.8×10-11에서 1.1×10-10 사이 수준으로 상대적으로 유사한 것을 확인하였다. 이는 시각 원간 시각차가 포함된 시각비교 측정치의 분석 시, Flicker Frequency Modulation (FFM)에 의해 일반적으로 1×106초 이후에 평균시간 $\tau$에 대해 $\tau^{+1}$기울기를 보이는 것과 대조되며, 이를 통해 시각비교 측정치를 이중 차분함으로써, 시각비교 측정치간 공통 시각 원 성분이 소거되었음을 확인할 수 있다.
본 논문에서는 이중 차분 TCH을 통해 시각비교 링크에 따른 성능 분석을 수행하였으며, 이를 통해 시각비교 링크 간 TDEV 및 MDEV 성능을 비교하였다. 4.1절에서 산출한 이중 차분 측정치를 활용하여 Eq. 8을 적용하였으며, TDEV 산출 결과는 Fig. 7과 같다.
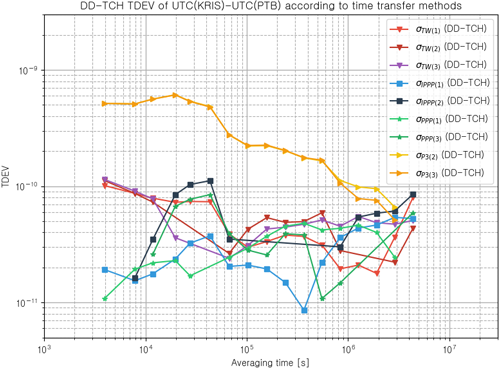
Fig. 7. DD-TCH TDEV of UTC(KRIS)-UTC(PTB) according to time transfer methods.
Fig. 7을 통해 TWSTFT, GPS IPPP, PPP, P3의 시각비교 링크에 대한 TDEV 수준을 확인할 수 있으며, TCH Case 별 평가 결과의 편차가 존재함을 확인하였다. TWSTFT, GPS P3의 경우 TCH Case 간 평가 결과의 차이가 상대적으로 낮으나, GPS IPPP와 GPS PPP의 경우 TCH Case 간 높은 편차를 보였다. TCH Case 2번과 3번의 경우, GPS P3가 포함되어 있어, 이중 차분 TCH 산출 시 상대적으로 열화된 TDEV 수준을 갖는 $-\sigma_{TW,P3}^{2}$ 성분이, 단기 TDEV이 상대적으로 우수한 GPS IPPP와 PPP의 평가에 활용되어, 약 1×10-10 수준의 범프(bump)가 도출된 것으로 추정된다. 이는 TCH 분석 시 유사한 안정도를 가지는 데이터를 대상으로 수행하여야 기대하는 평가결과를 도출하는 특성 때문이며, TWSTFT와 GPS IPPP, PPP 대비 GPS P3가 상대적으로 큰 불안정성을 갖기 때문인 것으로 판단된다.
또한 동일하게 Eq. 8을 활용하여 이중 차분 TCH 기반의 MDEV 평가를 수행하였으며, 이에 대한 결과는 Fig. 8a와 같다. 이중 차분 TCH 기반 MDEV 평가를 통해 시각원의 영향을 배제한 시각비교 링크의 주파수 안정도를 평가할 수 있으며, 각 시각비교 링크에 따라 서로 다른 단기 MDEV 수준을 보이나, 2×106초 이후에는 1.4×10-17에서 8.5×10-17 범위의 MDEV로 유사한 성능을 보임을 확인하였다. 이와 대조하여, Fig. 8b와 같이 시각원 간 영향이 포함된 MDEV의 경우, 시각원의 FFM 성분에 의해 2×105초 이후는 8×10-16 수준의 $\tau^{0}$ 기울기가 나타남을 확인하였다.
Fig. 8의 이중 차분 TCH 기반의 MDEV 평가 결과를 Fig. 9와 같이 시각비교 링크 종류에 따라 재 분류 하여 도시하였으며, 비교를 위해 시각원의 영향 포함된 MDEV 분석 결과를 각 시각비교 링크에 따라 포함하였다.
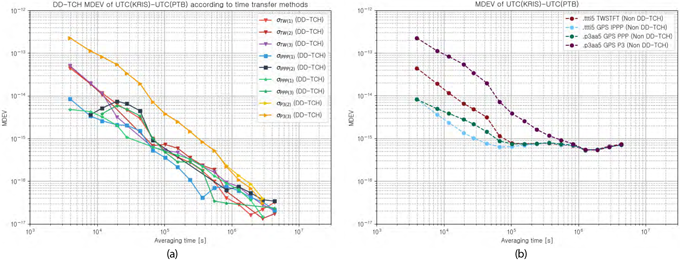
Fig. 8. DD-TCH Modified Allan Deviation (MDEV) of UTC(KRIS)-UTC(PTB) according to time transfer methods. (a) DD-TCH MDEV of UTC(KRIS)-UTC(PTB) as time transfer methods and TCH cases (b) MDEV of UTC(KRIS)-UTC(PTB) as time transfer methods using *ttti5 and *p3aa5 data.
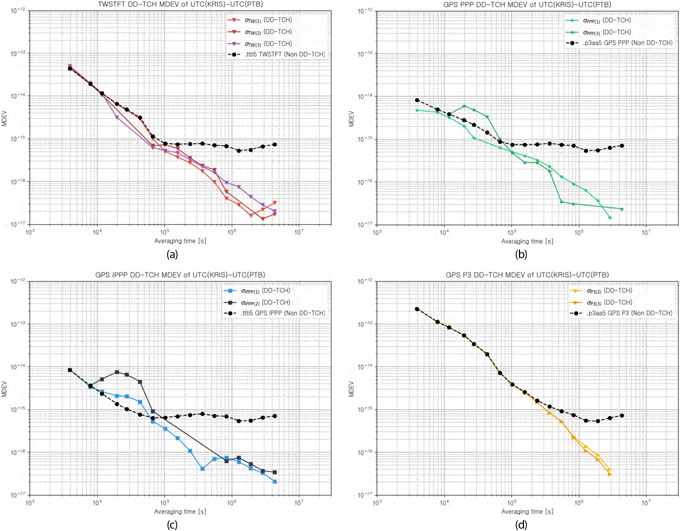
Fig. 9. DD-TCH MDEV of UTC(KRIS)-UTC(PTB) according to time transfer methods (compare with Non DD-TCH Results). All results are compared with and without DD-TCH: (a) TWSTFT MDEV, (b) GPS PPP MDEV, (c) GPS IPPP MDEV, and (d) GPS P3 MDEV.
TWSTFT 링크는 Fig. 9a와 같이, 이중 차분 TCH 기반 분석이 아닌 경우, 1×105초 이후에서 FFM 성분이 관찰되나, 이중 차분 TCH기반 분석 결과는 동일 시점 이후에도 $\tau^{-1}
$ 기울기를 유지하는 것을 확인하였다. GPS IPPP 와 PPP의 경우, TWSTFT의 경우에 비하여 단기 MDEV 및 기울기가 미세한 차이를 보이나, Figs. 9b,c와 같이 TWSTFT와 유사한 추이를 보였고, 이중 차분 TCH 분석 시 시각원 성분이 배제된 평가가 이루어 졌음을 확인하였다. 또한 Fig. 9d의 GPS P3 결과에서는 4×103초에서 1×10-13 수준의 상대적으로 열화된 주파수 단기 안정도를 가짐에 따라, 1×106초 이후에 FFM이 관찰되나, 이중 차분 TCH 분석의 경우 이전 시점과 동일한 수준의 기울기가 유지됨을 확인하였다.
결과적으로 이중 차분 TCH 기반의 TDEV 및 MDEV 평가를 통해 시각원의 영향이 배제된 객관적인 시각비교 링크의 평가가 가능함을 확인하였으며, 한국표준과학연구원과 독일의 PTB 간의 시각비교 링크가 NIST에서 수행한 UTC(USNO)와 UTC(NIST) 간 시각비교 링크의 성능과 유사한 mid 10-17 수준의 MDEV 성능을 가짐을 확인하였다.
본 논문에서는 한국표준과학연구원에서 운용 중인 TWSTFT, GPS IPPP, PPP, P3 기반 시각비교 기술을 소개하고, 일반적인 TCH 및 본 논문에서 활용한 이중 차분 측정치 기반 TCH 분석 방법을 제시하였다. 각 시각비교 시스템은 서로 다른 RF 활용, 측정치 생성 방식 및 보정 처리 방식을 갖으며 이에 따라 서로 다른 오차 특성을 갖는다. 또한 일반적으로 시각비교 측정치의 성능 분석은 시각비교 시스템의 특성과 시각원 간 시각 차 영향이 포함된 상태로 수행되며, 시각비교 링크의 객관적인 성능평가가 어려운 한계를 갖는다. 이러한 시각비교 측정치 특성을 고려하고 기존의 성능평가 방법의 한계를 극복하여 시각비교 링크만의 객관적인 안정도를 도출하기 위해, 미국 NIST에서는 이중 차분 TCH 평가 방법을 활용한 바 있으며, 이를 통해 미국 내 시각비교 링크의 mid 10-17 수준의 MDEV 성능을 가짐을 확인하였다.
본 논문에서는 한국표준과학연구원과 독일 PTB 간 운용되고 있는 TWSTFT, GPS IPPP, PPP, P3 기반 시각비교 링크에 대해 이중 차분 TCH 기반의 TDEV 및 MDEV의 안정도 평가를 수행하였으며, 시각 원 특성이 포함된 전통적인 시각비교 성능분석 결과와 대조하였다. 분석 결과, 이중 차분 TCH 기반의 TWSTFT, GPS IPPP, PPP, P3의 모든 MDEV 결과에서 전체 평균시간에 대해 시각원의 영향이 배제된 $\tau^{-1}$에 근접한 기울기를 확인하였으며, 2×106초 이후에 mid 10-17 수준으로 NIST의 시각비교 링크 성능과 유사한 성능을 가짐을 확인하였다.
본 논문에서 분석한 이중 차분 TCH 기반의 시각비교 링크의 성능분석 결과는 고 정밀 시각비교 및 동기를 요구하는 국가표준시, 금융, 국방, 전력, 지상파항법시스템, 위성항법시스템 등의 시각비교 기술 우선순위 설계 및 시각비교 링크 구축에 따른 성능평가 등에 활용 가능할 것으로 기대되며, 객관적인 시각비교 링크의 성능평가를 통해 기존 링크의 유지보수에도 활용할 수 있을 것으로 예상된다.
이 논문은 2025년도 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임 (RS-2024-00407003, 지상파항법시스템 고도화 기술개발사업).
Conceptualization & methodology & software, J. Lee; formal analysis & investigation, J. K. Lee; writing, J. Lee, J.-I. Oh, Y.-J. Heo; review and editing, J. H. Rhee, G. W. Choi, D.-H. Yu, M.-S. Heo; supervision, S.-h. Yang, M.-S. Heo; project administration, Y. K. Lee.
The authors declare no conflict of interest.
BIPM 2020, Establishment of International Atomic Time and Coordinated Universal Time, https://www.bipm.org/documents/20126/59466374/6_establishment_TAR20.pdf
Cheng, P., Shen, W., Sun, X., Cai, C., Wu, K., et al. 2022, Measuring Height Difference Using Two-Way Satellite Time and Frequency Transfer, Remote Sensing, 14, 451. https://doi.org/10.3390/rs14030451
Defraigne, P. & Petit, G. 2015, CGGTTS-Version 2E: an extended standard for GNSS time transfer, Metrologia, 52, G1. https://doi.org/10.1088/0026-1394/52/6/G1
Fang, M. & Ma, C. 2025, Uncertainty and quality assessment of satellite-based precipitation products using three-cornered hat method, Proceedings of SPIE, International Conference on Remote Sensing, Surveying, and Mapping (RSSM 2025), Xi’an, China, 25 June 2025, https://doi.org/10.1117/12.3066605
He, X., Xu, T., Xia, Y., Bateni, S. M., Guo, Z., et al. 2020, A Bayesian Three-Cornered Hat (BTCH) Method: Improving the Terrestrial Evapotranspiration Estimation, Remote Sensing, 12, 878. https://doi.org/10.3390/rs12050878
ITU-R TF.1153 2015, Technical document of ITU-R (The operational use of two-way satellite time and frequency transfer employing pseudorandom noise codes), ITU-R TF.1153-4. https://www.itu.int/dms_pubrec/itu-r/rec/tf/R-REC-TF.1153-4-201508-I!!PDF-E.pdf
Jiang, Z., Lewandowski, W., & Matsakis, D. 2005, UTC time transfer by IPPP, Proceedings of the 36th Annual Precise Time and Time Interval (PTTI) Meeting, Washington D.C., USA, 7-9 December 2004, pp.91-102.
Parker, T. E., Zhang, V., Petit, G., Yao, J., Brown, R. C., et al. 2022, A three-cornered hat analysis of instabilities in two-way and GPS carrier phase time transfer systems, Metrologia, 59, 035007. https://doi.org/10.1088/1681-7575/ac6a95
Petit, G. & Jiang, Z. 2008, Precise point positioning for TAI computation, International Journal of Navigation and Observation, 2008, Article ID 562878. https://doi.org/10.1155/2008/562878
Sjoberg, J. P., Anthes, R. A., & Rieckh, T. 2021, The Three-Cornered Hat Method for Estimating Error Variances of Three or More Atmospheric Datasets. Part I: Overview and Evaluation, Journal of Atmospheric and Oceanic Technology, 38, 555-572. https://doi.org/10.1175/JTECH-D-19-0217.1
Vernotte, F., Addouche, M., Delporte, J., & Brunet, M. 2004, The Three Cornered Hat Method: An Attempt to identify some Clock Correlations, 2004 IEEE International Ultrasonics, Ferroelectrics, and Frequency Control Joint 50th Anniversary Conference, Montreal, QC, Canada, 23-27 August 2004, pp.482-485. https://doi.org/10.1109/FREQ.2004.1418506