1Department of Aerospace Engineering and Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Korea
2Korea Aerospace Research Institute, Daejeon 34133, Korea
†Corresponding Author: Byungwoon Park, E-mail: byungwoon@sejong.ac.kr
Citation: Kim, S., Oh, J., Park, B., Park, H., & Ju, J.-M. 2025, EKF-Based Orbit Determination Simulation for a Lunar Satellite Using Multi-GNSS Observables, Navigation, and Timing, 14, 241-257.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 241-257. https://doi.org/10.11003/JPNT.2025.14.3.241
Received on Aug 10, 2025, Revised on Aug 24, 2025, Accepted on Aug 25, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
The Moon is increasingly recognized as a strategic waypoint for future Mars and deep space missions and this is driving demand for reliable Position, Navigation, and Timing (PNT) services. Traditional reliance on the Deep Space Network (DSN) provides high post-processed accuracy but limited real-time performance and may not scale with rising mission numbers. To address this, space agencies are exploring Global Navigation Satellite System (GNSS)-based and dedicated lunar navigation systems. Recent demonstrations, such as the Lunar GNSS Receiver Experiment (LuGRE) mission, have validated GNSS positioning at the Moon with kilometer-level accuracy. This study extends these efforts by simulating lunar orbit determination using multi-GNSS constellations. An Extended Kalman Filter (EKF) approach, integrating GNSS observations with orbital dynamics, is employed. The simulation results show significantly improved position accuracy and underscore EKF’s potential for future lunar navigation systems.
Lunar PNT, GNSS, EKF, orbit determination
달은 미래 유인 화성 탐사 및 심우주 탐사의 중간 거점으로써 주목받고 있으며, 향후 10년간 400건 이상의 달 관련 임무가 예상되고 있다 (ISECG 2024, Kawade & Christodoulopoulou 2024). 이처럼 급격히 증가하는 임무들의 수요에 맞춰 안정적인 임무 수행과 성공을 위한 달에서의 Position, Navigation, and Timing (PNT) 서비스 제공의 중요성도 함께 증가하고 있다. 현재까지 오랜 기간 사용된 가장 보편적인 심우주 항법 기술로는 지상 안테나와의 양방향 통신 기반으로 위치를 결정하는 Deep Space Network (DSN)이며, 후처리 과정을 통해 수 m 수준의 위치 정확도를 가지는 것으로 알려져 있다 (Delépaut et al. 2022). 하지만 앞으로 계속 증가하는 임무 수요를 인프라 공급이 따라가지 못할 것으로 전망하고 있으며, 수 m 수준의 정확도는 후처리로만 가능할 뿐, 실시간으로 처리를 하는 경우 위치 오차는 수 km 수준으로 떨어지게 된다 (Giordano et al. 2021a, 2021b).
전세계적으로 National Aeronautics and Space Administration (NASA), European Space Agency (ESA) 그리고 Japan Aerospace Exploration Agency (JAXA)와 같은 주요 우주국들은 달에서의 안정적인 항법 서비스 제공을 위한 계획을 수립하고 있으며, 지구 Global Navigation Satellite System (GNSS) 항법 신호를 달에서 획득하여 사용하는 방법과 지구 GNSS와 같이 달에서 독자적으로 운영할 수 있는 위성 항법 시스템을 구축하고자 하는 방법에 대해 활발히 연구하고 있다. GNSS를 달 임무에서 활용하는 것은 기존 존재하는 시스템을 활용하는 것이므로 시스템 구성이 비교적 단순하고 큰 수정 없이 사용할 수 있기 때문에 운영 복잡성과 비용 절감 측면에서 장점이 있는 것으로 여겨진다 (Giordano et al. 2021b). 또한 NASA Artemis 프로그램의 일환으로 NASA는 달에서 통신과 항법 서비스 제공을 위한 인프라 체계 이른바 LunaNet을 제안하고 이를 구축하기 위해 노력하고 있다 (Israel et al. 2020). 그리고 미래에 LunaNet에 참여하게 될 여러 서비스 제공자들 사이의 상호운영성을 보장하기 위해 NASA, ESA, JAXA 주도하에 LunaNet Interoperability Specification과 같이 LunaNet 통신, 항법 서비스와 관련 표준을 명시하는 기술 문서 작성을 지속하고 있다 (Giordano et al. 2023, Dafesh et al. 2025).
이러한 과정 속에서 2025년 2월 NASA의 Commercial Lunar Payload Service 프로그램의 일환으로 Firefly사의 Blue Ghost Mission 1 탑재체로 선정된 Lunar GNSS Receiver Experiment (LuGRE) 수신기가 최초로 달에서 지구 GPS, Galileo 신호를 수신하여 위치 결정까지 성공하였다 (ASI 2025). 명확한 궤도 결정 방식이 설명되지는 않았지만 위치 정확도는 약 1.5 km 정도로 나온 것으로 확인이 되었다. 이는 GPS, Galileo 측정치로 Least square 기반 단독 측위를 수행했을 때 수 km 위치 오차가 도출된 다른 시뮬레이션 결과와 일맥상통한다 (Capuano et al. 2016).
본 논문에서는 GPS, Galileo 위성군만 고려한 기존 연구와 대비해서 현존하는 모든 위성군을 달 위성 궤도 결정에 활용하는 시뮬레이션 구성 방식에 대해 구체적으로 논의한다. 그리고 GNSS 측정치를 활용한 궤도 결정에서 지구와 달 사이의 편향된 기하학적 분포로 인해 측정치의 작은 오차 성분도 위치 정확도에 큰 영향을 줄 수 있는 Least square 기반 측정치 단독 측위 방식 대신에 측정치 모델과 위성 궤도 동역학 모델을 결합한 Extended Kalman Filter (EKF) 방식으로 궤도 결정 시뮬레이션을 진행하였다. EKF 기반 궤도 결정으로 수 km 오차 수준인 LuGRE 결과 대비 크게 향상된 위치 정확도를 얻었다.
궤도 결정을 위한 지구 GNSS 위성 측정치 생성을 하려면 우선 달 궤도에 위치한 위성에서 가시 GNSS 위성을 판별할 필요가 있다. Fig. 1과 같이 지구와 달 사이는 약 400,000 km 떨어져 있어 지구 GNSS 위성 신호가 모두 같은 방향에서 도달하게 되며, Main lobe에 해당하는 강한 신호는 대부분 지구에 가려지고 일부 main lobe 신호와 상대적으로 세기가 약한 Side lobe 영역의 신호가 달 위성에 도달할 수 있다. 시뮬레이션 측정치 생성에서 가시 위성 판별을 위해 link budget 수식으로부터 위성 신호의 반송파 대 잡음비를 계산하여 활용하며, Eq. (1)과 같다 (Parker et al. 2022).
$$\frac{C}{N_0}
= P_T + G_T(\varphi,\theta) + G_R(\varphi,\theta)
– 10\log(k\,T_{\mathrm{sys}})
– 20\log\left(\frac{4\pi d}{\lambda_f}\right)
– LM$$
여기서 $P_{T},\ G_{T}(\varphi,\theta),\ G_{R}(\varphi,\theta)$는 각각 GNSS 위성의 신호 출력 세기와 신호의 시선 방향 벡터가 GNSS 안테나 그리고 수신기 안테나와 이루는 각도에 따른 안테나 이득이다. $\varphi,\theta$는 시선 방향 벡터가 안테나 좌표축과 이루는 방위각과 Off-boresight angle이다. Off-boresight angle은 안테나가 지향하는 쪽 방향의 축과 시선 방향 벡터가 이루는 각도이다. $d,\lambda_{f}$는 GNSS 위성 안테나와 수신기 안테나 사이의 기하학적인 거리와 $f$ 주파수 신호의 파장 길이이다. $k,T_{sys}$는 볼츠만 상수와 system noise temperature이며, system noise temperature는 Eq. (2)와 같이 신호를 수신하는 안테나와 수신기의 noise temperature의 합으로 나타난다 (Popescu 2017, Donaldson et al. 2020).
$$T_{sys} = T_{ant} + T_r$$
여기서 $LM$은 polarization losses, receiver implementation losses 등을 포함한 마진이다.
Link budget을 계산하여 가시 위성을 판단할 때 기하학적 제약조건, 신호 세기, 위성의 상대적인 자세 그리고 신호 복조 이렇게 네가지 사항을 고려하였다. 기하학적 제약조건은 신호가 지구나 달에 의해 물리적으로 차폐되지는 않는지 판단하고, 신호 세기는 link budget으로 계산된 신호의 세기가 수신기가 감지할 수 있는 최소 수신 세기인지를 판단한다. 그리고 신호가 단순히 다른 행성에 의해 차폐되는 경우 외에도 지구 GNSS 위성의 송출 안테나와 달 위성의 수신 안테나가 지향하는 상대적인 방향에 따라 안테나 이득 패턴이 다르므로 위성 자세에 따른 안테나 이득 패턴의 영향도 link budget 계산에서 고려해야 한다. 마지막으로 GNSS 위성 신호로부터 위치 결정을 수행하기 위해서는 신호를 송출하는 위성에 대한 Clock & Ephemeris Data (CED)를 최소한 가지고 있어야 하며 이를 항법 신호로부터 직접 복조 하여 얻는 상황을 고려한다. 본 논문에서 시뮬레이션 시 고려한 위성군과 위성군별 신호 종류는 Table 1과 같다.
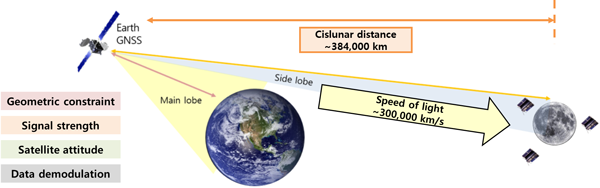
Fig. 1. GNSS-Lunar satellite relative geometry and visibility.
Table 1. Considered constellations and signal types.
| System | Signal 1 | Signal 2 |
|---|---|---|
| GPS GLONASS Galileo BDS QZSS IRNSS | L1CA G1CA E1-B B1I L1CA L5-SPS | L5-I G2CA E5a-I B3I L5-I – |
$P_T$와 $G_T$의 합을 Equivalent Isotropic Radiated Power (EIPR)라고 정의하며, EIRP는 GNSS 위성에서 송출된 신호의 세기와 관련된 값이다. GPS, Galileo, QZSS 위성군은 EIRP와 관련한 정보를 공식적으로 공개하고 있다 (Marquis & Reigh 2015, Cabinet Office 2023, Menzione et al. 2024).
GPS Block IIR, IIR-M, III는 록히드 마틴사에서 제작하였으며, 해당 위성군에 대한 안테나 이득 패턴 정보를 전체 Off-boresight angle 영역에 걸쳐 제공하지만 보잉사에서 제작한 GPS Block IIF 위성군에 대한 안테나 이득 패턴 정보는 제한된 영역의 일부 Off-boresight angle에 대해서만 제공된다 (Navigation Center 2022). NASA에서는 GPS L1에 대한 안테나 이득 패턴 복원 프로젝트인 Antenna Characterization Experiment (ACE)를 진행한바 있으며, GPS Block IIF 위성군까지 전체 Off-boresight angle 영역에 대한 안테나 이득 패턴 정보를 제공한다 (Donaldson et al. 2020). L5 신호의 경우, GPS Block III는 L1과 마찬가지로 전체 Off-boresight angle 영역에 대해 정보가 공개되어 있으며, GPS Block IIF의 경우에는 L1 안테나 이득 패턴 정보 스케일링을 통해 활용할 수 있다 (Delépaut et al. 2020). Figs. 2와 3은 각각 GPS Block IIR, IIR-M L1 안테나 이득 패턴과 GPS Block III L1/L5 안테나 이득 패턴을 시각화한 것이다.
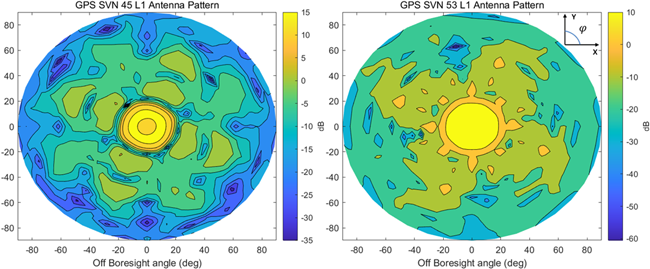
Fig. 2. GPS Block IIR, IIR-M L1 antenna gain pattern.
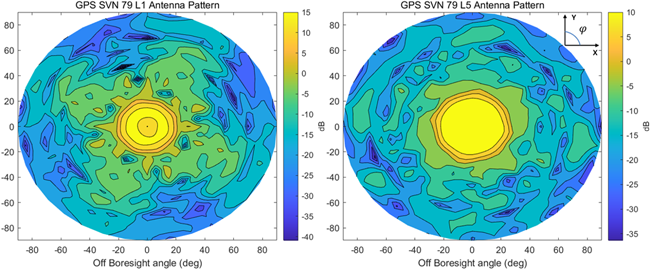
Fig. 3. GPS Block III L1/L5 antenna gain pattern.
GPS 위성군별 $P_T$ 값은 ACE 프로젝트나 다른 달 위성 궤도 결정 시뮬레이션 연구에서 사용한 값들을 참조할 수 있다 (Winternitz et al. 2019, Donaldson et al. 2020, Parker et al. 2022). 본 논문에서 GPS L1CA 신호의 출력 값은 실제 지상 안테나에서 측정한 반송파 대 잡음비로부터 위성별로 도출한 연구 결과를 활용한다 (Wang et al. 2018). Wang et al. (2018)은 GPS Block IIR부터 IIF까지 L1CA 신호에 대한 $P_T$값을 측정하였으며, 각 GPS 위성군별 평균값을 시뮬레이션에서 적용하였다. 이때 GPS Block III의 신호 출력 세기는 GPS Block IIR-M과 동일하다고 가정하였다. L5 신호 출력의 경우 GPS Interface Control Document (ICD)에서 L5-I 신호의 최소 수신 세기를 L1CA 보다 GPS Block IIF는 0.6 dBW 높게 그리고 GPS Block III는 1.5 dBW 높게 명시하고 있으므로 해당 차이만큼 더해진 값을 출력 신호 세기로 사용한다 (SAIC 2022).
Galileo는 Full Operational Capability (FOC) 위성군에 대한 EIRP 패턴 정보가 각 측정치 주파수 대역에 대해 공개되어 있다 (Menzione et al. 2024). Fig. 4는 Galileo E1과 E5a 신호에 대한 EIRP 패턴 정보를 시각화한 것이다. 또한 E1, E5a 신호의 E1-B 신호와 E5a-I 측정치 신호는 각각의 전체 신호 출력 세기에서 50%에 해당하는 Power sharing으로 인한 신호 손실을 고려해야 한다 (Teunissen & Montenbruck 2017).
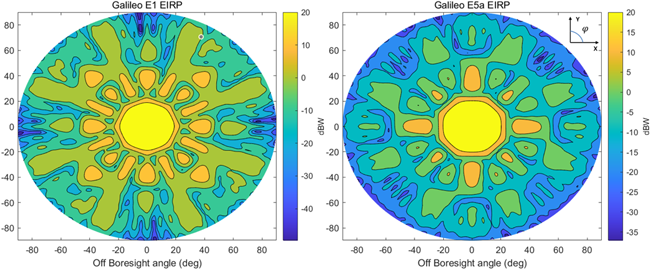
Fig. 4. Galileo FOC E1/E5a EIRP.
QZSS는 GPS와 유사하게 안테나 이득 패턴 정보를 공개하고 있다 (Cabinet Office 2023). Fig. 5는 QZSS L1과 L5 신호의 안테나 이득 패턴을 나타낸다. QZSS 위성의 L1CA 신호 출력 세기는 QZSS 기반 Geostationary Earth Orbit (GEO) 궤도 결정 시뮬레이션 연구에서 사용된 값을 참조하였다 (Nakajima & Yamamoto 2024). GPS, Galileo, QZSS를 제외한 나머지 위성군에 대한 EIRP 관련 시뮬레이션 설정 파라미터는 위성 궤도 형상에 따라 GPS, QZSS 위성군의 데이터를 활용하였다. GLONASS의 위성 신호 출력 세기와 안테나 이득 정보는 GPS Block III 정보를 활용하였고 BDS 위성군의 신호 출력 세기는 BDS3 Medium Earth Orbit (MEO) 위성의 B3I 신호 출력 세기를 일괄적으로 적용하였다 (Wang et al. 2022). BDS 위성군은 MEO, Inclined Geosynchronous Orbit (IGSO), GEO로 구성되어 있으므로 MEO는 GPS Block III, IGSO와 GEO는 QZSS Block II와 Block III 위성 안테나 정보를 각각 활용하였다. 마지막으로 IRNSS의 출력세기는 QZSS L1CA와 동일하다고 가정하였으며, IRNSS는 IGSO와 GEO로 구성되어 BDS와 마찬가지로 안테나 이득 정보는 QZSS Block II와 Block III 정보를 각각 활용하였다. 상세한 내용은 Tables 2와 3에 정리하였다.
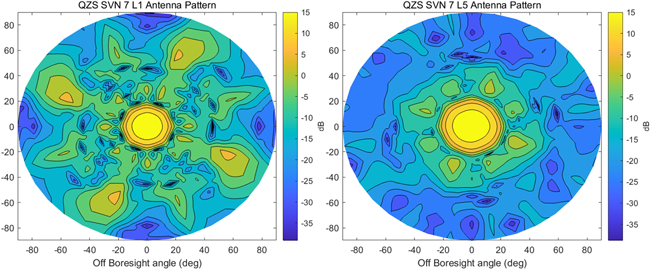
Fig. 5. QZSS L1/L5 antenna gain pattern.
Table 2. Signal transmission power per signal.
| System | Signal 1 | Power (dBW) | Power share (dBW) | Signal 2 | Power (dBW) | Power share (dBW) | Note |
|---|---|---|---|---|---|---|---|
| GPS GLONASS Galileo BDS QZSS IRNSS | L1CA G1CA E1-B B1I L1CA L5-SPS | 16.53 16.53 EIRP 15 14.1 14.1 | 0 0 3 0 0 0 | L5-I G2CA E5a-I B3I L5-I – | 18.03 18.03 EIRP 15 15.6 – | 0 0 3 0 0 – | GPS Block III GPS Block III FOC BDS3 – QZSS L1CA |
Table 3. Antenna gain pattern per signal.
| System | Signal 1 | ANT | Signal 2 | ANT | Not |
|---|---|---|---|---|---|
| GPS GLONASS Galileo BDS MEO BDS IGSO BDS GEO QZSS IRNSS | L1CA G1CA E1-B B1I B1I B1I L1CA L5-SPS | GPS L1 GPS L1 EIRP GPS L1 QZSS L1 QZSS L1 QZSS L1 QZSS L5 | L5-I G2CA E5a-I B3I B3I B3I L5-I – | GPS L5 GPS L5 EIRP GPS L5 QZSS L5 QZSS L5 QZSS L5 – | GPS Block III GPS Block III FOC GPS Block III QZSS Block II & III QZSS Block II & III QZSS Block II & III QZSS Block II & III |
지구 GNSS 위성의 위성 자세 모델은 일반적으로 Yaw-steering 자세 모델과 Orbit-normal으로 분류된다 (Montenbruck et al. 2015). Yaw-steering 자세 모델은 Fig. 6과 같이 GNSS 위성의 방송용 안테나가 항상 지구 중심을 향한 상태로 안테나 Boresight 방향을 회전축으로 회전하는 자세 모델이다. Yaw-steering 자세 모델에 있는 위성은 태양 전지판의 회전축이 태양 방향과 수직이 되도록 안테나 Boresight 방향에 대해 회전한다. International GNSS Service (IGS)에서 정의하는 위성 동체 좌표계는 Z축을 안테나 Boresight 방향, Y축을 위성 태양 전지판의 회전축으로 정의한다 (Montenbruck et al. 2015). Yaw-steering 자세 모델은 일반적으로 MEO, IGSO 위성에서 평상시 자세 모델로 사용한다. 또한 태양이 가려지는 특수한 상황에서는 위성별로 특별한 기동을 수행하는데, 본 논문에서는 모든 MEO, IGSO 위성은 Yaw-steering 자세 모델을 유지한다고 가정하였다.

Fig. 6. Yaw-steering attitude model.
Orbit-normal 자세 모델은 태양의 위치와 상관없이 IGS에서 정의하는 위성 동체의 좌표계상 Y축이 위성 궤도면과 항상 수직인 상태로 고정되어 있다. 일반적으로 GEO 위성이 해당 자세 모델을 사용하므로, 본 논문에서도 GEO 위성은 orbit-normal 자세 모델을 적용하였다.
달 환경에서 지구 GNSS 신호를 활용하는 방안에 대해 분석하는 많은 문헌에서 GNSS 신호 수신 안테나를 항상 지구 중심을 향하는 상황을 가정한다 (Winternitz et al. 2019, Delépaut et al. 2020, Giordano et al. 2021b). 지구 GNSS 신호 가용성을 확인하고 정확한 위치 결정을 수행하는 목적으로는 안테나가 항상 지구 중심을 향하는 것이 가장 적합하다. 하지만 지구 GNSS 위성과 같이 달 위성이 항법 위성으로 역할을 수행한다면 앞서 설명한 두가지 자세 모델과 유사한 자세 모델을 가질 가능성이 있으며, 이경우 GNSS 안테나가 항상 지구 중심을 향하는 것은 제한이 있을 수 있다. 본 논문에서는 지구 GNSS 가시성 확보와 달 위성 항법 서비스 제공이라는 두가지 측면을 고려하여, 지구 GNSS 위성의 Yaw-steering 자세 모델과 유사한 자세 모델을 정의하여 시뮬레이션에 적용하였다. Fig. 6에서 지구 위성의 Yaw-steering 자세 모델의 경우, 위성 동체 X 축의 + 방향이 YZ 평면을 기준으로 태양이 있는 방향으로 향하게 되는 것을 확인할 수 있다. 이러한 특성에서 착안하여 태양 대신 지구 방향과 위성 동체의 Y축이 수직이 되도록 하는 Yaw-steering 자세 모델을 정의하였고 Eqs. (3-5)와 같다.
$$\vec{e}_{Z} = -\frac{\vec{r}}{\lVert \vec{r} \rVert}$$
$$\vec{e}_{Y}=\frac{\vec{e}_{\mathrm{Sat}\rightarrow\mathrm{Earth}}\times\vec{r}}{\lVert \vec{e}_{\mathrm{Sat}\rightarrow\mathrm{Earth}}\times\vec{r}\rVert}$$
$$\vec{e}_{X} = \vec{e}_{Y} \times \vec{e}_{Z}$$
여기서 $\vec{r}$는 달에 대한 달 위성의 상대 벡터이고 $\vec{e}_{\mathrm{Sat}\rightarrow\mathrm{Earth}}$는 달 위성에서 지구로의 단위 벡터를 의미한다. Fig. 7은 달 위성의 달 주변 지점별 위성 자세를 시각적으로 나타낸다. 이러한 자세 모델을 가지는 달 위성의 지구 GNSS 수신 안테나는 위성 동체의 +X 방향을 Boresight 방향으로 부착되어 있다고 설정하였다. 수신 안테나는 2×2 Microstrip patch antenna array를 사용한다고 가정하였으며, Fig. 8은 L1 신호의 수신 안테나 이득 패턴을 시각화한 것이다.

Fig. 7. GNSS-like yaw-steering attitude model.
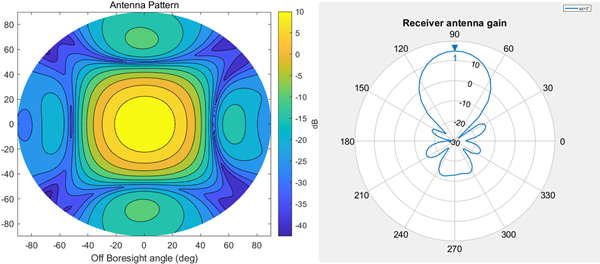
Fig. 8. Receiver L1 antenna gain pattern.
GNSS 항법 신호를 측정치로 활용하기 위해서는 해당 신호를 송신한 위성에 대한 위치 및 위성 시계에 대한 정보를 알고 있어야 한다. Fig. 9는 달 위성이 지구 GNSS 항법 신호로부터 측정치를 얻는 과정을 간략하게 나타낸다. GNSS 반송파 신호에는 위성의 위치정보와 시계오차 정보와 같이 항법에 반드시 필요한 정보와 알마낙과 같이 항법에 반드시 필요하지는 않지만 도움이 되는 정보가 항법 메시지 형태로 함께 포함되어 있다. 전체 항법 메시지를 수신하는 데에는 GPS L1CA에서 제공하는 LNAV의 경우 12.5분이 필요하며, 대부분의 항법 메시지가 전체 데이터를 받기 위해서는 상당한 시간이 필요하다. 그러나 항법에 필요한 CED 정보를 수신하기 위해 전체 항법 메시지를 모두 받을 필요는 없으며, 모든 항법 메시지가 CED 정보를 효율적으로 제공하기 위해 일정한 주기를 가지고 방송된다 (Kim et al. 2024a).
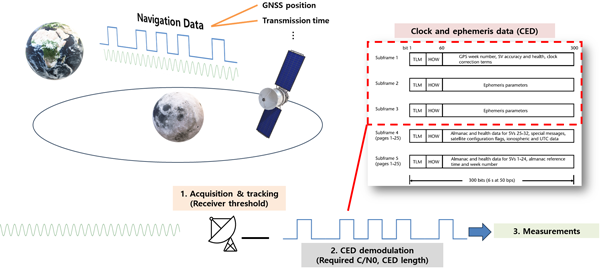
Fig. 9. Acquisition of signals and CED demodulation.
달 위성에 탑재된 GNSS 수신기가 감지할 수 있는 세기보다 높아 GNSS 신호 획득에 성공한 후에는 복조 과정을 통해 반송파에 실려 있는 항법 메시지를 획득한다. 복조 과정에서 CED에 오류가 발생할 수 있으며, 이경우 해당 CED는 위치 결정에 사용할 수 없다. 항법 메시지의 성능 평가 지표 중 하나로 CED error rate을 사용하는데, 이로부터 특정 항법 메시지의 CED를 복조하는데 필요한 최소 신호 수신 세기를 판단할 수 있다 (Anghileri et al. 2013, Noh et al. 2022, Dafesh et al. 2025). CED error rate은 CED를 수신하는 동안 CED 데이터에서 오류가 발생할 확률을 의미하며, 이 확률이 일정 수준 이하가 되는 수신 세기를 항법 메시지 수신을 위한 최소 수신 세기로 사용한다. 또한 앞서 설명한 바와 같이 CED 데이터는 주기적으로 반복 방송되며, 항법 메시지 종류별로 정해진 데이터 길이가 있지만 메시지 종류별로 조금씩 다른 길이를 가지고 있고 데이터를 수신하는 데에 걸리는 시간은 신호를 수신한 시점에 영향을 받으므로 시뮬레이션에서 CED 데이터를 수신하는데 필요한 최소 시간에 대한 분석이 필요하다. Noh et al. (2022)는 Anghileri et al. (2013)의 연구를 참고하여 주요 GNSS 위성군 신호의 항법 메시지별 CED error rate에 따른 최소 신호 수신 세기와 최소 수신 시간을 각각 Robustness와 Time-to-first-fix-data (TTFFD) 지표로 분석하였다. Tables 4와 5에 시뮬레이션에서 가시 위성 판별을 위해 적용한 항법 메시지 종류별 최소 수신 세기 및 최소 수신 시간을 정리하였다.
Table 4. Robustness of each navigation message.
| System | Ephemeris | Required C/N0 (dB-Hz) | Note | Ephemeris | Required C/N0 (dB-Hz) | Note |
|---|---|---|---|---|---|---|
| GPS | LNAV | 24.9 | – | CNAV | 23.6 | – |
| GLONASS | NAV | 26.36 | – | – | – | – |
| Galileo | INAV | 27.4 | – | FNAV | 20.6 | – |
| BDS | D1 | 24.7 | – | D2 | 34.7 | – |
| QZSS | LNAV | 24.9 | GPS | CNAV | 23.6 | GPS |
| IRNSS | SPS | 21.1 | – | – | – | – |
Table 5. TTFFD of each navigation message.
| System | Ephemeris | TTFFD (s) | Note | Ephemeris | TTFFD (s) | Note |
|---|---|---|---|---|---|---|
| GPS | LNAV | 35.5 | – | CNAV | 29.6 | – |
| GLONASS | NAV | 30 | – | – | – | – |
| Galileo | INAV | 31.6 | – | FNAV | 59.4 | – |
| BDS | D1 | 35.5 | – | D2 | 35.5 | – |
| QZSS | LNAV | 35.5 | GPS | CNAV | 29.6 | GPS |
| IRNSS | SPS | 59.2 | – | – | – | – |
Noh et al. (2022)의 연구에서 분석되지 않은 GLONASS와 QZSS 위성군 신호에 대해서 GLONASS의 경우 최소 수신 신호 세기를 Dafesh et al. (2025)에서 항법 메시지 및 신호 설계 과정에서 사용한 수식으로부터 Bit Error Rate (BER)을 계산하였으며, TTFFD는 GLONASS NAV 메시지의 CED 길이와 같다고 가정하였다. QZSS의 L1CA LNAV, L5-I CNAV는 구조와 형태가 GPS와 유사하므로 GPS와 같다고 가정하였다. 마지막으로 BDS는 B1I와 B3I 신호에서 D1, D2 항법 메시지를 제공하는데 MEO, IGSO 위성은 D1 항법 메시지를 방송하며, GEO 위성은 D2 항법 메지지를 제공한다 (CSNO 2019). BDS GEO 위성의 D2 전송 속도는 500 bps로 50 bps인 D1 보다 10배 빠른 속도로 제공된다. 전송 속도가 더 빠른 D2에 대해서는 Noh et al. (2022)에서 분석한 D1 최소 수신 세기 결과에서 전송 속도 증가에 따른 BER 증가 영향을 반영하여 산정하였다 (Anghileri et al. 2013). D1과 D2의 CED 구조와 방송 주기는 유사하므로 D1 TTFFD 결과를 D2에 동일하게 적용하였다. 시뮬레이션에서 가시 위성을 판단하기 위해 수신된 신호가 수신기 최소 수신 세기 보다 높으며, 동시에 유효한 항법 메시지가 있는지 확인한다. 수신기가 신호를 획득하였으나 유효한 항법 메시지가 없는 경우 앞서 설명한 기준을 통해 CED 복조 가능성을 판단하여 최종적으로 가시성을 결정한다. CED 복조 가능성은 수신된 신호의 세기가 수신되고 있는 신호가 제공하는 항법 메시지의 Robustness를 만족하는 최소 수신 세기보다 같거나 높은 최초의 시점에서 연속적으로 TTFFD 시간 동안 유지되는지를 확인한다. 다시 말해서 항법 메시지의 Robustness를 만족하는 최소 수신 세기이상의 신호 세기가 TTFFD 동안 유지되면 해당 신호는 항법 메시지를 수신한 것으로 간주한다. 그 이후로 해당 항법 메시지의 유효 기간 동안 신호의 세기가 수신기 민감도 보다만 높다면 해당 신호를 송신한 위성은 가시 위성으로 판단한다.
가시위성에 대한 측정치 생성에서 고려된 오차 성분은 GNSS 위성의 방송궤도력 또는 CED 오차, 전리층 지연, 사용자 시계 오차 그리고 측정치 잡음이다. 이 중에서 GNSS 위성의 방송궤도력 오차는 실제 방송궤도력으로 구한 위성 위치 및 시계 정보와 정밀궤도력으로 구한 위성 위치 및 시계 정보의 오차를 주기 함수 형태로 모델링하여 사용하였다. Eq. (6)은 방송궤도력 위성 위치 오차와 위성 시계 오차를 모델링하기 위해 Curve fitting에 사용된 주기 함수이다 (Long & Stacey 2025).
$$e(t)=A(0)+\sum_{i=1}^{N} \left[ A(2i-1)\cos\left(\frac{2\pi}{T_i}t\right)+A(2i)\sin\left(\frac{2\pi}{T_i}t\right) \right]$$
여기서 $A(i)$는 주기 함수에서 curve fitting을 통해 얻는 계수이고, $T_i$는 모델링하고자 하는 함수의 주기이다. 하루 간격의 데이터를 curve fitting하여 계수 정보를 처리하고, 계수 정보를 여러 날짜에 대해 저장하여 궤도 결정 시뮬레이션에서 임의의 날짜의 계수 정보를 사용하도록 설정해 GNSS 위성의 방송궤도력 오차를 반영하였다. Fig. 10은 GPS Block III 위성의 방송궤도력 오차를 계수로 도출한 뒤에 이를 다시 주기 함수를 통해 계산한 결과이다.
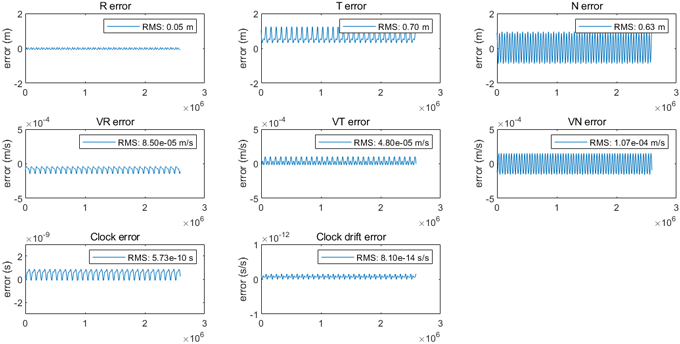
Fig. 10. Modeled ephemeris errors of GPS Block III.
지구 GNSS 위성에서 달 위성으로 도달하는 신호가 전리층을 통과하는 비율이 상대적으로 작을 수 있으나 신호가 전리층을 2번 통과하게 된다면 그 오차는 지상 사용자의 경우보다 훨씬 큰 값을 가질 수 있다. 일반적으로 지상 사용자는 전리층을 특정 고도에 위치한 얇은 하나의 막형태로 모델링하여 값을 산출할 수 있지만, 다음과 같이 전리층을 2번 통과하는 경우 해당 모델로 전리층을 모델링하는 것은 불가능하다. 그러므로 본 논문에서는 특정 고도에 위치한 전리층의 최고 전자 밀도 값으로 전체 고도 영역으로 모델링하는 modified Chapman profile로 고도에 따른 전자 밀도를 모델링하여 GNSS 위성 신호 벡터가 통과하는 전리층 영역의 전자 밀도를 계산하고 이를 수치적으로 적분하는 방식으로 전리층 지연을 측정치 생성에 포함하였다 (Long & Stacey 2025). Fig. 11은 modified Chapman profile로 고도 350 km를 기준으로 고도 1000 km까지 전자 밀도 비율을 모델링한 예시를 나타낸다. 최대 전자 밀도의 고도와 전리층 영역은 사용자 입력으로 변경할 수 있다. Fig. 12는 전리층 지연 계산 결과의 예시를 나타낸다. 적게는 수십 m에서 크게는 수백 m 수준까지 전리층 지연의 영향이 나타나는 것을 확인할 수 있다. 전리층 지연에 의한 오차 포함시 가시위성의 극단적인 치우침으로 인해 측위오차가 매우 커질 가능성이 있다. 따라서, 본 연구에서는 궤도 결정시 방송궤도력으로 구한 지구 GNSS 위성 위치와 추정된 달 위성의 위치로부터 지구 고도 500 km 이내 영역을 통과하는 신호는 배제함으로써 전리층 지연이 포함된 측정치는 제외하도록 하였다.
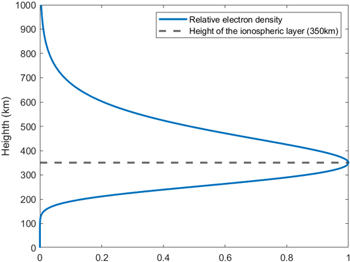
Fig. 11. Relative electron density from modified Chapman profile.
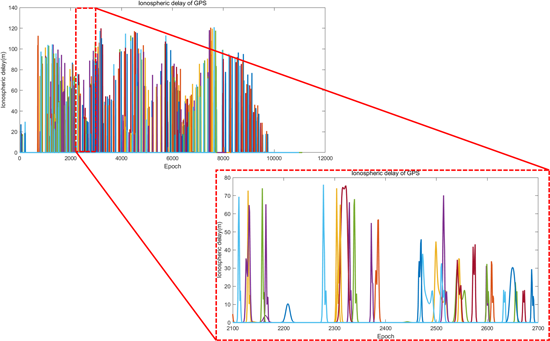
Fig. 12. Ionospheric delay calculation result.
사용자 시계 오차는 2차 방정식 형태 모델에 시계 오차의 랜덤 특성을 반영하도록 Eq. (7) 형태로 모델링하였다 (Long & Stacey 2025).
$$\begin{bmatrix}
\delta t(t_{k+1})\\
\dot{\delta t}(t_{k+1})\\
\ddot{\delta t}(t_{k+1})
\end{bmatrix}
=
\begin{bmatrix}
1 & \Delta T & \frac{\Delta T^2}{2}\\
0 & 1 & \Delta T\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\delta t(t_k)\\
\dot{\delta t}(t_k)\\
\ddot{\delta t}(t_k)
\end{bmatrix}
+
L
\begin{bmatrix}
\varepsilon_1\\
\varepsilon_2\\
\varepsilon_3
\end{bmatrix}$$
여기서 $\delta t,\ \dot{\delta t},\ \ddot{\delta t}$는 시계 오차, 시계 오차의 변화율 그리고 시계 오차 가속도 항이다. $\Delta t$ 시간 간격 뒤에 시계 오차 상태 벡터는 기본적으로 2차 방정식 형태로 구성되며, 랜덤 특성은 표준 정규 분포를 따르는 랜덤 변수로 이루어진 벡터 $[ \varepsilon_1\ \ \varepsilon_2\ \ \varepsilon_3 ]^T$와 process noise 공분산 행렬 $P$로부터 얻어진다. $L$은 대칭인 행렬 $P$가 있을 때, $P$ 행렬을 Eq. (8)과 같이 Cholesky 분해하여 얻어지는 상삼각행렬이다 (Bhattarai 2015, Long & Stacey 2025).
$$P = L L^{T} =
\begin{bmatrix}
q_1 \Delta T + q_2 \frac{\Delta T^{3}}{3} + q_3 \frac{\Delta T^{5}}{20} &
q_2 \frac{\Delta T^{2}}{2} + q_3 \frac{\Delta T^{4}}{8} &
q_3 \frac{\Delta T^{3}}{6} \\
q_2 \frac{\Delta T^{2}}{2} + q_3 \frac{\Delta T^{4}}{8} &
q_2 \Delta T + q_3 \frac{\Delta T^{3}}{3} &
q_3 \frac{\Delta T^{2}}{2} \\
q_3 \frac{\Delta T^{3}}{6} &
q_3 \frac{\Delta T^{2}}{2} &
q_3 \Delta T
\end{bmatrix}$$
여기서 $q_1$은 시계 오차의 process noise 분산의 변화율, $q_2$는 시계 오차 변화율 process noise 분산의 변화율 그리고 $q_3$는 시계 오차 가속도 process noise 분산의 변화율이다. 순서대로 시계의 랜덤 특성 중에서 frequency white noise, frequency random walk 그리고 frequency random run과 관련되어 있다. 본 논문에서 달 위성은 루비듐 원자 시계를 사용한다고 가정한다. Fig. 13은 루비듐 원자 시계를 가정하고 시계 오차 상태 벡터를 시간에 대해 전파한 예시 결과를 도시한다.
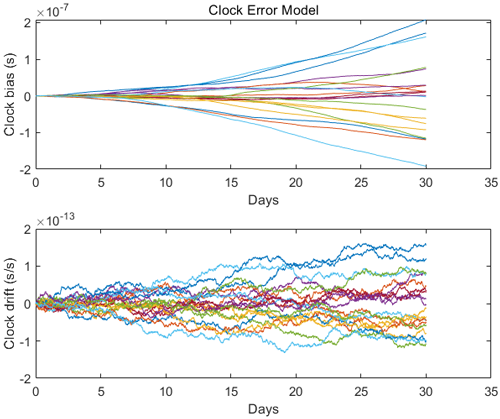
Fig. 13. Result of rubidium atomic clock error modeling.
가시 위성에 대한 측정치 생성 부분에서 의사거리 측정치 그리고 의사거리 변화율 또는 도플러 측정치를 고려한다. 의사거리 측정치의 측정치 잡음은 의사거리 측정치 복조 방법별 Delay Lock Loop (DLL) thermal noise jitter로 모델링한다. DLL thermal noise jitter 모델로 얻은 표준편차 정규분포를 따르는 잡음을 측정치에 포함한다. GPS L1CA와 같이 Binary Phase-Shift Keying (BPSK) 복조 방식을 사용하는 측정치는 Eq. (9)와 같이 모델링할 수 있다 (Kaplan & Hegarty 2017).
$$\sigma_{DLL,BPSK}
=
\begin{cases}
c \cdot T_c \; \sqrt{
\frac{B_n}{2\,C/N_0}\,
D\left[1+\frac{2}{T_c\,C/N_0\,(2-D)}\right]
},
& D \ge \frac{\pi R_c}{B_{fe}}
\\[16pt]
c \cdot T_c \; \sqrt{
\frac{B_n}{2\,C/N_0}
\left(
\frac{1}{B_{fe}T_c}
+ \frac{B_{fe}T_c}{\pi -1}
\left(
D-\frac{1}{B_{fe}T_c}
\right)^2 \right)
\left[ 1+\frac{2}{T_c\,C/N_0\,(2-D)}\right]
},
& \frac{R_c}{B_{fe}} < D < \frac{\pi R_c}{B_{fe}}
\\[16pt]
c \cdot T_c \; \sqrt{
\frac{B_n}{2\,C/N_0}
\left(
\frac{1}{B_{fe}T_c}
\right)
\left[ 1+\frac{1}{T_c\,C/N_0}\right]
},
& D \le \frac{R_c}{B_{fe}}
\end{cases}$$
BPSK 방식 이외에 Binary Offset Carrier (BOC), Composite Binary Offset Carrier (CBOC) 방식을 사용하는 측정치의 잡음 모델은 모두 BOC thermal noise jitter를 사용한다 (Julien et al. 2010, Jin et al. 2012, Teunissen & Montenbruck 2017). BOC의 thermal noise jitter는 Eq. (10)과 같다.
$$\sigma_{\mathrm{DLL,\,BOC}(n,m)}
=
c \cdot T_c
\sqrt{
\frac{
B_n
}{
2\left(4\frac{n}{m}-1\right)\frac{C}{N_0}
}
\,D
\left[
1 + \frac{1}{T\frac{C}{N_0}}
\right]
}$$
마지막으로 도플러 측정치 생성에서는 측정치 잡음 모델로 Frequency Lock Loop (FLL) thermal noise jitter를 사용하였으며, Eq. (11)과 같다 (Kaplan & Hegarty 2017).
$$\sigma_{\mathrm{FLL}}
=
\frac{\lambda_L}{2\pi T}
\sqrt{
\frac{
4 F B_n
}{
\frac{C}{N_0}
}
\left[
1 + \frac{1}{T\frac{C}{N_0}}
\right]
}$$
여기서 $B_n$은 Loop noise bandwidth, $\frac{C}{N_0}$ 는 Hz 단위로 표시된 측정치 대 잡음비, $T$는 predetection integration time, $D$는 early-to-late correlator spacing, $\lambda_{L}$은 반송파 파장 길이, $B_{fe}$는 double-sided front-end bandwidth, $T_c$는 chip period, $R_c$는 chipping rate 그리고 $c$는 빛의 속도이다. 본 논문의 시뮬레이션에서 설정한 달 위성의 GNSS 수신기는 WeakHEO 그리고 LuGRE 수신기 파라미터를 참조하였으며, Table 6에 정리하였다 (Capuano et al. 2016, Parker et al. 2022). 본 논문에서 L5와 같이 Data 신호인 I와 Pilot 신호인 Q를 모두 제공하는 신호에 대해서는 I 신호만 사용한다고 가정하였으며, Pilot 신호 사용에 따른 predilection integration time 증가는 구분 없이 Table 6에서 제시한 값을 모두 동일하게 적용하였다. 또한 Table 6에서 double-sided front-end bandwidth는 L1과 L5에 대해서만 제시하였으나 실제 시뮬레이션에서 B1, B3, G1, G2와 같이 다른 주파수 영역의 신호에 대한 값도 따로 지정하여 진행하였다.
Table 6. Receiver parameters.
| Parameter | Value |
|---|---|
| Bn | 0.5 Hz |
| T | 0.02 s |
| D | 0.3 chips |
| Bfe,L1 | 2 · 12.276 MHz |
| Bfe,L5 | 2 · 10.23 MHz |
Fig. 14는 지구에서 달로 이동하는 과정 동안 지구 GNSS 위성 가시성과 가시 위성수에 따른 Geometric Dilution of Precision (GDOP)를 시뮬레이션한 것이다. 본 시뮬레이션은 궤도 결정과는 무관하게 지구에서 달까지 이동하는 동안 달 위성이 경험하는 지구 GNSS 신호 수신 환경을 도시하기위해 진행하였다. 그러므로 해당 시뮬레이션에서 항법 메시지 복조는 고려하지 않았으며, 신호의 수신 세기가 수신기 민감도 이상인 경우 가시 위성으로 판단하였다. 수신기 민감도는 23 dB-Hz로 설정하였고, 지구 GNSS 수신 안테나는 항상 지구 중심을 향하는 상황으로 진행하였다. 결과 그래프로부터 알 수 있는 바와 같이 위성의 위치가 달 근처에 도달한 지점에서 가시 위성수가 희박하고, GDOP는 수천 정도의 값을 가진다. 이러한 GDOP로부터 측정치에 포함된 m 수준의 오차가 위성의 위치 오차에서는 km 수준으로 영향을 미칠 수도 있다. 측정치 단독으로 least square 기반 위치 결정을 달 궤도 결정에서 사용하기에는 정확도가 심각하게 떨어질 수 있다 (Capuano et al. 2016).
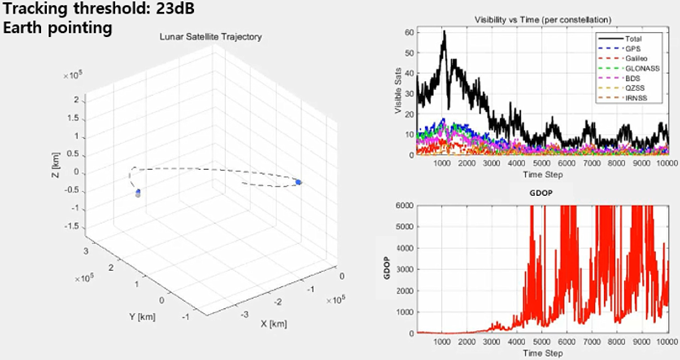
Fig. 14. Satellite visibility and GDOP variation during Lunar transfer.
그러므로 측정치 단독 least square 기반 위성 궤도 결정 방식 대신 측정치와 위성 역학 모델을 함께 결합하는 EKF 기반 궤도 결정 방식을 사용한다. 달 궤도 환경과 같이 위성 가시성이 열악하면서 신호의 기하학적 분포가 좋지 않은 상황에서도 역학 모델 기반 궤도 예측 과정으로 안정적으로 궤도 결정을 수행한다.
궤도 추정에서 추정하고자 하는 상태 벡터는 Eq. (12)와 같이 정의한다.
$$\vec{X}
=
\begin{bmatrix}
x \quad y \quad z \quad v_x \quad v_y \quad v_z \quad C_r \quad
\delta t_1 \quad \cdots \quad \delta t_n \quad \dot{\delta t}
\end{bmatrix}^{T}$$
순서대로 위성 위치, 위성 속도이며, $C_r$은 태양 복사압 계수이다. $\delta t_1$은 GPS L1CA 측정치 바이어스가 동화된 사용자 시계 오차를 나타내며, $\delta t_n$까지 Table 1에 정리한 측정치 종류만큼 측정치 바이어스가 동화된 사용자 시계 오차가 추정 변수로 정의된다. 이러한 이유로는 측정치 종류별로 위성과 수신기 모두 고유한 하드웨어 바이어스를 가지게 되는데, 이러한 바이어스는 직접적인 추정이 어렵고 수신기 바이어스는 추정 과정에서 사용자 시계 오차에 동화된다 (Teunissen & Montenbruck 2017). 또한 위성군 시스템 사이에도 시계오차에 동화된 측정치 바이어스가 존재한다. 마지막으로 $\dot{\delta t}$는 사용자 시계 오차 변화율이다.
EKF는 time update 과정과 measurement update 과정을 반복적으로 수행하며, time update 과정에서 궤도 예측을 진행하고 time update에서 발생한 예측 오차를 measurements update 과정에서 측정치를 통해 보상한다. EKF time update에서 위성 위치와 속도는 수치 적분으로 계산하고 상태 벡터에 대한 공분산 행렬을 함께 예측하며 Eqs. (13, 14)와 같다.
$$\hat{X}_{k+1}^{-} = f\!\left( \hat{X}_{k} \right)$$
$$P_{k+1}^{-}
=
\Phi(k+1,k)\, P_{k}\, \Phi(k+1,k)^{T}
+
Q$$
여기서 상첨자 -는 예측 과정으로 얻어진 값을 의미한다. $P$는 상태 벡터의 공분산 행렬이며, $Q$는 프로세스 잡음 행렬이다. $\Phi(k+1,k)$는 이전 시점에서 다음 시점으로의 상태 천이 행렬이며, Eq. (15)와 같이 궤도 역학 부분과 시계 오차 부분으로 분류할 수 있다.
$$\Phi(k+1,k)
=
\begin{bmatrix}
\Phi(k+1,k)_{\text{dynamics}} & 0 \\
0 & \Phi(k+1,k)_{\text{clock}}
\end{bmatrix}$$
상태 천이 행렬 계산에서 위성 궤도 역학 부분은 비선형이므로 수치적 미분 방식을 통해 계산하였으며, 시계 오차 부분은 상태 벡터의 미분 방정식 계수 행렬을 선형화해서 계산하였다.
Measurement update 과정에서 사용된 측정치는 의사거리 및 도플러 측정치이며, Eqs. (16, 17)과 같이 모델링하여 관측 행렬 계산에 사용하였다.
$$\rho_{r,f}^{\,s}
=
d_{r}^{\,s}
–
\delta t_{f}^{\,s}
+
\delta t_{r,f}
+
\varepsilon$$
$$\dot{\rho}_{r,f}^{\,s}
=
\dot{d}_{r}^{\,s}
–
\dot{\delta t}^{\,s}
+
\dot{\delta t}_{r}
+
\varepsilon$$
여기서 $d_r^s$와 $\dot{d}_{r}^{s}$는 각각 GNSS 위성과 달 위성 사이의 기하학적 거리와 거리의 변화율이며, $\delta t_f^s\delta$와 $\delta t_{r,f}$는 각각 GNSS 위성 시계 오차와 달 위성 시계 오차이다. 하첨자 $r$, $f$는 각각 달 위성과 사용한 측정치 종류를 의미한다. 상첨자 $s$는 지구 GNSS 위성을 의미한다. 측정치 생성에서 전리층 지연에 의한 오차를 포함하였으나 궤도 결정 시뮬레이션에서는 이를 별도로 추정하거나 보상하지 않는다. 대신에 계산된 GNSS 위성 위치와 달 위성 위치로부터 신호 벡터가 전리층을 통과한다고 판단되는 측정치는 measurement update 과정에서 제외하고 관측행렬과 칼만 이득을 계산하였다. Measurement update 과정에서 칼만 이득 계산, 상태 벡터 업데이트 그리고 공분산 행렬 업데이트 일련의 과정은 Eqs. (18-20)과 같다.
$$K_k
=
P_k^- H^{T}
\left( H P_k H^{T} + R \right)^{-1}$$
$$\hat{X}_k
=
\hat{X}_{k}^{-}
+
K_k \left( z_k – h\!\left( \hat{X}_{k}^{-} \right) \right)$$
$$P_k
=
P_k^{-}
–
K_k H P_k^{-}$$
여기서 $K_k$는 칼만 이득, $H$는 측정치 선형화를 수행한 관측 행렬, $R$은 측정치 잡음 행렬 마지막으로 $z_k$와 $h(\hat{X}^-_k)$는 각각 측정치 벡터와 측정치 모델링식으로부터 이를 예측 계산한 측정치 모델 벡터이다.
Fig. 15는 시뮬레이션에서 가시성 분석과 궤도 결정을 위한 측정치 생성에 활용한 지구 GNSS 위성군 구성을 나타낸다. 위성군은 GPS, GLONASS, Galileo, BDS, QZSS, IRNSS 총 6개로 구성되어 있으며, 궤도 파라미터는 International Committee on GNSS (ICG) booklet에 기재되어 있는 위성군별 궤도 파라미터를 참조하였다(United Nations Office for Outer Space Affairs 2021). 총 위성수는 123개이며, 위성군별로 GPS 27개, GLONASS 24개, Galileo 24개, BDS 30개, QZSS 7개, IRNSS 11개로 구성된다.
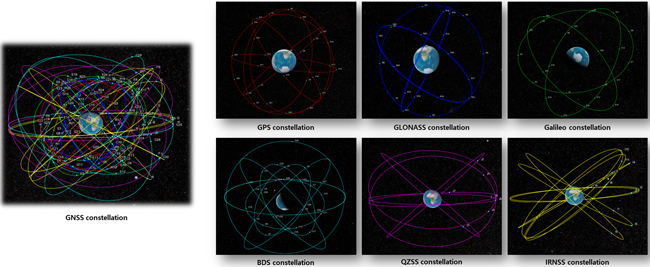
Fig.15. GNSS constellation in simulation.
마찬가지로 Fig. 16은 시뮬레이션에서 사용자에 해당하는 달 위성의 두가지 궤도 형상을 나타낸다. Fig. 16의 왼쪽은 Elliptical Lunar Frozen Orbit (ELFO), 오른쪽은 Near Rectilinear Halo Orbit (NRHO)로 두 궤도 모두 큰 이심률을 가진다. ELFO는 JAXA에서 실제로 계획중인 LNSS 위성군의 후보 궤도 파라미터 중 하나를 참조하였으며, NRHO는 Lunar gateway의 임무 궤도 후보 중 하나를 선택하여 활용하였다 (Williams et al. 2017, Murata et al. 2024). 궤도 주기는 ELFO가 약 12시간, NRHO가 약 7일을 가진다.
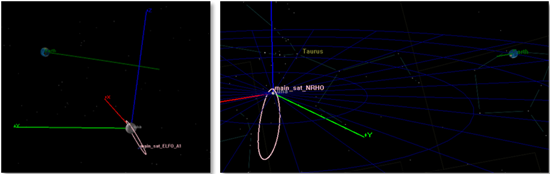
Fig.16. Lunar satellite in ELFO (left) and in NRHO (right).
시뮬레이션은 총 30일의 기간에 대해 진행하였으며, 위성의 자세 모델은 앞서 설명했던 것과 같이 지구 GNSS와 유사한 Yaw-steering 모델을 가지는 것으로 가정하였으며, 지구 GNSS 위성 신호 수신 안테나는 위성 동체의 +X축 방향으로 부착되어 있는 것으로 가정하였다. 달에서 운영되는 위성이라는 특수성과 기술 적용 시점에 따른 진화를 고려하여 위성의 수신기 민감도는 앞선 지구-달 이동 시뮬레이션과 달리 15 dB-Hz로 설정하였으며, 측정치 생성시 앞서 설명한 기준에 따라 항법 메시지 복조를 추가적으로 고려하였다. Table 7은 측정치 생성에서 사용한 달 위성의 실제 궤적을 전파하는데 적용한 역학 모델과 궤도 결정 시뮬레이션에서 EKF time update 때 궤도 예측으로 적용한 역학 모델의 차이를 도시한다. 실제 궤도의 궤적을 전파하는데 적용한 역학 모델보다 궤도 예측에서 적용한 역학 모델을 의도적으로 열하시켜 모델의 부정확성에 의한 영향을 고려할 수 있도록 하였다.
Table 7. Dynamic model.
| Parameter | True trajectory | Prediction |
|---|---|---|
| Gravitational potential |
10 Degree 10 Order LP165P |
4 Degree 4 Order LP165P |
| Third body attraction | Sun, Earth, Jupiter, Mars, Venus | Sun, Earth |
| Solar radiation pressure | Yes | Yes |
먼저 Figs. 17과 18은 각각 NRHO에서 30일 시뮬레이션 기간 동안 위성군별 신호 종류별 평균 가시 위성수와 전체 위성군에 대한 평균 가시 위성수를 나타낸다. 마찬가지로 Figs. 19와 20은 같은 결과를 ELFO에 대해 도시한 것이다. 시뮬레이션 결과, NRHO에서의 평균 가시 위성 수는 6.401개로 나타났으며, ELFO에서는 3.596개로 나타나, NRHO가 ELFO에 비해서 약 2.805개(약 78%) 더 많은 가시 위성수를 가진다. 다시 말해, NRHO는 ELFO 대비 GNSS 위성 가시성이 약 1.78배 향상된 결과를 나타낸다. 이러한 이유는 궤도 형상에서 알 수 있으며 Fig. 16에서 ELFO는 지구의 위치와 관계없이 궤도면이 달 관성 좌표계에서 항상 일정한 방향을 향하고 있는다. 그에 반해 NRHO는 궤도면이 항상 지구 방향을 향하게 되는데, 이러한 특성으로 NRHO는 ELFO보다 상대적으로 지구 GNSS 위성 가시성 확보에 있어 유리하다고 볼 수 있다.
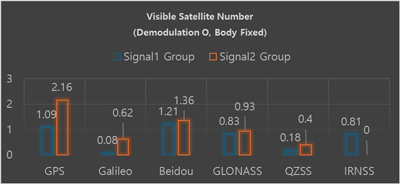
Fig.17. Satellite visibility from NRHO for each GNSS constellation.
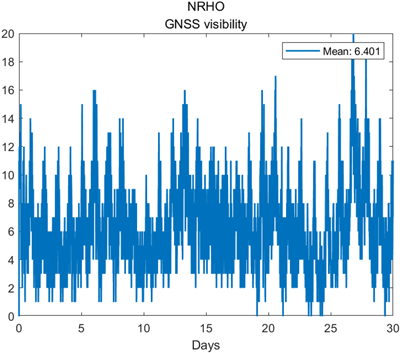
Fig.18. Mean satellite visibility from NRHO.
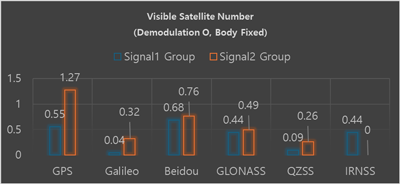
Fig.19. Mean satellite visibility from ELFO.
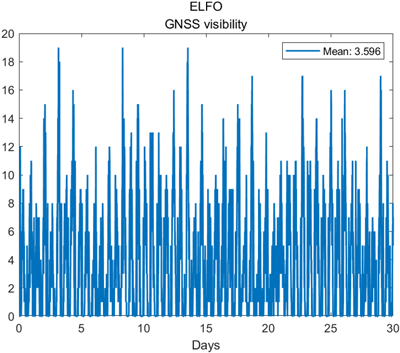
Fig.20. Mean satellite visibility from ELFO.
그리고 두 궤도 형상에서 공통적으로 Signal 2에 포함된 측정치가 Signal 1에 포함된 측정치 보다 상대적으로 높은 가시성을 나타낸다. Table 2에서 GPS L1, QZSS L1 신호의 출력 보다 L5신호의 출력이 1.5 dBW 높게 설정되어 있는데, 최소 수신 세기가 L5에 대해 높게 설정되어 있는 ICD 문서의 내용을 따른 것이다. 이는 나중에 공개된 L5의 신호의 세기가 L1보다 높은 특성을 반영한다 (Hrbek et al. 2016). GPS, Galileo, QZSS를 제외한 나머지 위성군은 GPS, QZSS 위성군의 데이터를 활용하였기 때문에, 전반적으로 GPS 결과와 유사한 경향성을 나타내고, 위성 궤도의 상이성에 따른 기하학적인 차이만 반영된 결과라고 할 수 있다. 또한 Galileo에 비해 상대적으로 높은 가시성을 나타내는 것도 신호 출력과 관련한 파라미터를 GPS와 동일한 데이터를 적용하였기 때문이지, 실제 결과는 상이할 수 있다. 그리고 Eq. (1)에서 $20 \text{log}(\frac {4\pi d}{\lambda_f })$는 자유 공간 신호 전파에 따른 신호 세기 감소를 나타내는데, 파장이 길수록 상대적으로 손실이 적게 나타난다. 그러므로 L1 보다 상대적으로 파장이 긴 L5 신호는 가시성 확보 측면에서 이점이 있다. 마지막으로 Table 4를 보면 Galileo의 경우 항법 메시지 복조를 고려하는 상황에서 E1-B로 방송되는 INAV보다 E5a-I로 방송되는 FNAV를 수신하기 위해 요구되는 최소 수신 신호 세기가 무려 7 dB-Hz 낮다. 그러므로 Galileo 역시 Signal 1 신호인 E1-B보다 Signal 2 신호인 E5a-I의 가시성이 상대적으로 높게 나타난다.
앞서 얻은 위성 가시성 환경을 가진 측정치 데이터를 가지고 EKF 기반 궤도 결정 시뮬레이션을 수행하였으며, Figs. 21과 22는 각각 NRHO와 ELFO의 궤도 결정 결과를 나타낸다. 각각의 그래프에서 왼쪽은 위성의 위치와 속도 오차를 도시하고, 오른쪽은 여러 위성 시계 오차 변수 중에서 GPS L1CA에 해당하는 시계 오차 결과와 시계 오차의 변화율 결과이다. 그래프에서 회색 음영은 위성의 가시성이 0인 구간을 의미하며, 파란 실선은 실제 오차 그리고 주황색, 보라색 점선은 공분산 행렬에서 얻은 표준편차 값의 3배인 $3\sigma$를 나타낸다. 마지막으로 붉은 세로 실선은 시뮬레이션이 종료되는 시점에서 Root Mean Square (RMS) 값을 계산하기 시작한 시점을 나타내며, NRHO는 시뮬레이션 종료 7일 전 구간에 대해 RMS 값을 계산하였고, ELFO는 시뮬레이션 종료 1일 전 구간에 대해 RMS 값을 계산하였다 두 궤도 형상에 대해 모두 위치는 50 m 이하 그리고 시계 오차는 30 ns 이하의 정확도를 보였다.
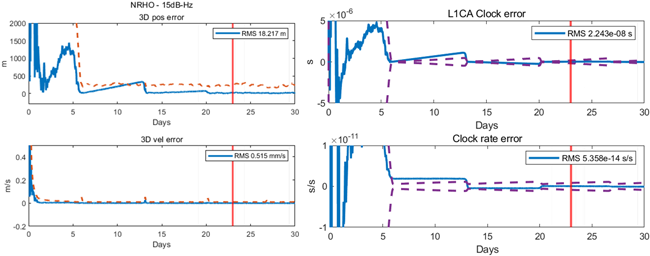
Fig. 21. Position and velocity errors (left) and clock errors (right) of NRHO.
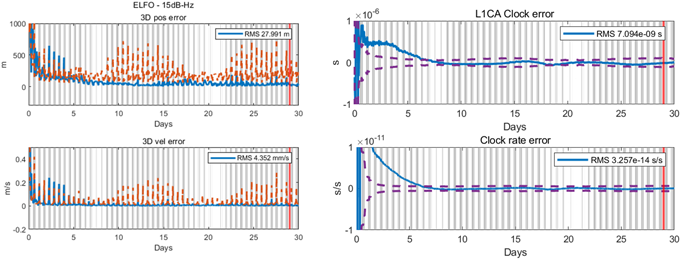
Fig. 22. Position and velocity errors (left) and clock errors (right) of ELFO.
NRHO, ELFO 모두 이심률이 큰 궤도이며, 두 궤도 형상에 대한 위치 오차 결과를 보면 공통적인 특징이 나타나는 것을 확인할 수 있다. 궤도 주기가 상대적으로 긴 NRHO의 결과 그래프인 Fig. 21을 보면 위치 오차가 궤도의 주기마다 계단 형태로 급격히 줄어드는 경향을 확인할 수 있다. 구체적으로 Fig. 21의 왼쪽 상단 그래프에서 시뮬레이션 시작 13일 부근에서 위치 오차가 약 330 m에서 6.5 m까지 급격히 줄어든다. 주기가 상대적으로 짧은 ELFO의 결과인 Fig. 22를 보면 시뮬레이션 초반 궤도 주기마다 NRHO와 동일하게 오차가 줄어드는 것을 확인할 수 있다. Fig. 23은 ELFO의 결과 그래프를 확대한 것이며, ELFO에서는 위치와 속도 오차가 급격히 증가하는 지점 전후로 측정치가 아예 들어오지 못하다가 잠깐 측정치가 들어올 때 NRHO와 유사하게 오차가 빠르게 줄어든다. NRHO, ELFO 두 궤도에서 이러한 현상이 나타나는 지점은 달과 위성 사이의 거리가 가장 가까워지는 근월점 부근이며, 근월점 부근에서 위성의 기동이 빨라지면서 동시에 위성의 동역학적 특성도 빠르게 변하게 되고 이것이 필터의 빠른 수렴을 야기한다 (Winternitz et al. 2019). 하지만 반대로 속도 오차는 근월점 부근에서 크게 튀는 현상이 있는데, 이는 근월점 부근에서의 빠른 동역학적 특성으로 궤도 예측 오차가 오히려 크게 발생하는 영향으로 볼 수 있다. 만일 근월점 부근에서 측정치가 들어오지 않아 궤도 예측만 지속하는 상황이라면 해당 지점에서 큰 위치 오차가 발생하게 될 것이다. 반면에 원월점 부근에서는 위성의 동역학적 특성이 낮은 탓에 측정치가 들어오더라도 위치 오차 개선에 큰 영향을 미치지 못하는 현상을 보인다. 이러한 현상은 이심률이 큰 NRHO, ELFO 두 궤도 형상에 대해 동일하게 나타났다.
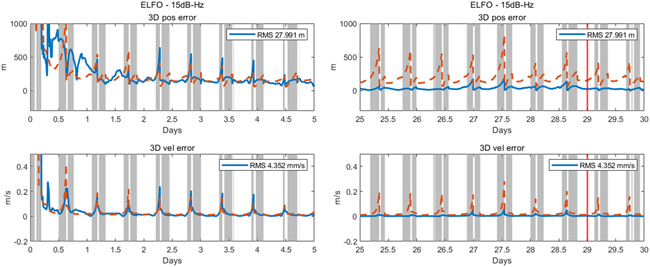
Fig. 23. Zoomed-in view of position and velocity errors of ELFO.
Table 8은 시뮬레이션 위치 오차 결과를 Radial, along-track, cross-track 방향을 포함하여 도시한 것이다. Radial은 달 중심에서 위성 방향, Along-track은 위성 진행 방향, Cross-track은 궤도면과 수직인 방향이며, 위성의 위치 오차를 사용자 측정치 시선 방향 벡터로 사영하였을 때, 큰 영향을 미치는 위성 위치 오차는 Radial 방향이다 (Montenbruck et al. 2018, Kim et al. 2024b). 향후 달 항법 위성의 궤도 오차 모델링이나 달 항법 위성의 궤도 오차가 사용자에게 미치는 영향을 분석하기 위해서는 관성 좌표계 좌표축 방향 오차 성분 보다는 radial, along-track, cross-track 방향으로 오차를 확인하는 것이 바람직하다. Winternitz et al. (2019)의 연구에서는 달과 지구의 편향된 기하학적 배치 구조가 위치와 속도에 미치는 영향을 분석하기 위해서 지구 중심에서 위성 쪽으로의 range 방향 오차, range 방향과 수직인 평면에 포함되는 lateral 방향에서의 오차로 나누어 결과를 제시하였다. Winternitz et al. (2019)의 연구에서 측정치가 들어오는 방향인 range 방향에서의 위성 위치 오차가 Lateral 방향보다 훨씬 작게 나타났다. Table 8에서 ELFO는 세 방향에서 뚜렷한 오차 경향이 나타나지는 않는 반면에, NRHO는 Cross-track 방향의 오차가 가장 작게 나타났다. Fig. 16의 NRHO 형상에서 궤도면과 지구 방향이 서로 수직한 모습인 것을 알 수 있는데, Winternitz et al. (2019)의 연구에서 range 방향 오차가 lateral 방향에 비해 작은 오차를 가진 것과 같이 NRHO에서는 측정치가 들어오는 방향인 Cross-track 방향의 오차가 가장 작게 나타나는 것으로 해석할 수 있다.
Table 8. Simulation results in RMS.
| Orbit | Position (m) | Velocity (mm/s) | Radial (m) | Along-track (m) | Cross-track (m) | L1CA clock (ns) |
|---|---|---|---|---|---|---|
| NRHO | 18.22 | 0.52 | 11.90 | 12.33 | 6.19 | 22.43 |
| ELFO | 27.99 | 4.35 | 13.53 | 13.24 | 20.62 | 7.09 |
마지막으로 Fig. 24는 LuGRE 미션과 유사하게 GPS L1, L5 그리고 Galileo E1, E5a 측정치만 사용하여 EKF 기반 궤도 결정을 수행한 결과를 NRHO에 대해 나타내며, Figs. 25와 26은 같은 조건으로 진행한 ELFO 결과 그래프이다. 이전 시뮬레이션 보다 측정치 종류와 가시 위성수가 상대적으로 부족하기 때문에 위치 오차가 비교적 크게 나타나지만, 이전 시뮬레이션에서 확인한 현상은 동일하게 관측된다. 측정치가 상대적으로 더 열악한 환경임에도 불구하고 두 궤도 형상에 대해 모두 위치는 50 m 이하 그리고 시계 오차는 50 ns 이하의 정확도를 보였다. 이는 현재까지 보고된 LuGRE 위치 오차인 1.5 km의 1/10 수준의 오차로, 그 정확도가 10배 이상 향상될 수 있음을 제시하였다.
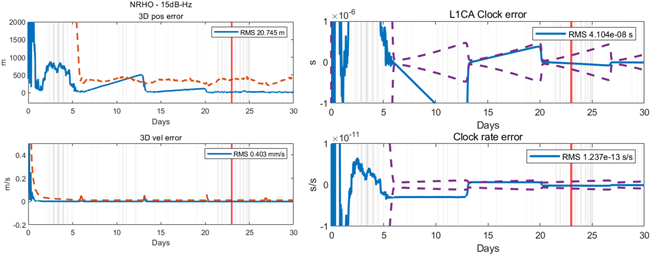
Fig. 24. Position and velocity errors (left) and clock errors (right) of NRHO with GPS and Galileo.
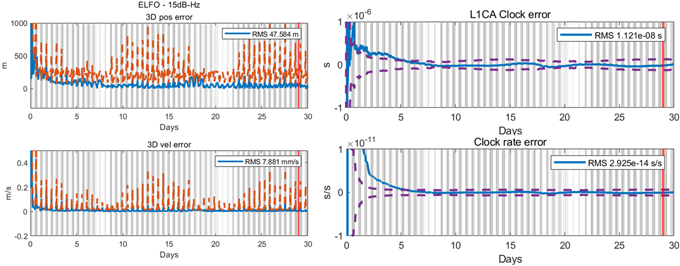
Fig. 25. Position and velocity errors (left) and clock errors (right) of ELFO with GPS and Galileo.
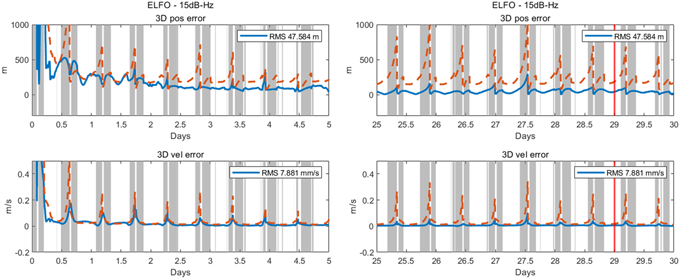
Fig. 26. Zoomed-in view of position and velocity errors of ELFO with GPS and Galileo.
본 논문에서는 지구 GNSS 위성 신호를 사용하여 달 위성의 궤도 결정을 시뮬레이션을 통해 진행하였다. GNSS 위성 신호 가시성 분석을 통해 L1 주파수 영역 신호보다 L5 주파수 영역 신호의 가시성이 더 높음을 확인하였다. 이는 L1보다 L5 신호가 나중에 설계된 신호이고, L5 신호 출력이 L1보다 높기 때문에 나타난 결과이다. 궤도 형상 별로는 궤도면이 관성 좌표계에 대해 일정한 방향을 가지는 ELFO 보다 궤도면에 지구 방향을 향하는 NRHO에서 더 높은 가시성의 신호 수신 환경을 보여주었다.
궤도 결정 시뮬레이션에서 NRHO, ELFO 두 가지 경우에 대해 모두 위치 정확도가 RMS 기준 50 m 이하로 달성할 수 있음을 확인하였다. 이는 평균 가시 위성수가 3~6개로 상대적으로 열악하고 GDOP가 최대 수천까지 나타나는 달 환경에서 유의미한 결과라고 볼 수 있다. 또한 이심률이 큰 궤도에서 근점에서의 높은 동역학적 특성이 궤도 예측과정에서 큰 오차를 야기할 수 있으나 측정치가 있는 경우 오히려 높은 동역학적 특성이 필터의 빠른 수렴을 이끌어내고, 원점에서는 반대로 낮은 동역학적 특성이 궤도 예측과정에서는 작은 오차를 가지더라도 필터의 수렴에는 큰 영향이 없는 것을 확인하였다.
본 연구를 통해 달에서 지구 GNSS 신호를 사용하여 궤도 결정을 수행하는 가능성에 대해 확인하였다. GPS, Galileo, QZSS를 제외한 다른 위성군에 대해 Link budget 계산과 위성군 방송궤도력 오차 모델링에서 정보가 존재하지 않거나 데이터 처리가 모두 이루어지지 않은 경우 궤도 형상이 유사한 GPS, Galileo, QZSS 위성군의 정보를 대신 가정하여 사용하였다. 추후 시뮬레이션 연구의 발전도 및 신뢰성 확보를 위해서는 본 연구에서 가정한 다른 위성군의 특성을 정확히 반영할 필요가 있다. 이를 위해 Kim et al. (2024b)에서 GPS, Galileo, QZSS, BDS 위성군에 대해 방송궤도력 오차를 통계적으로 분석한 것과 같이 GLONASS, IRNSS에 대한 방송궤도력 오차를 분석하여 모델링에 활용할 수 있을 것이며, Link budget 계산에 필요한 물리적 파라미터는 오픈 소스로 공개된 시뮬레이션 툴의 소스코드나 각 위성군별 ICD 문서 또는 IGS에서 제공하는 위성군 Metadata 문서 정보를 결합하여 개선할 수 있을 것이다 (Iiyama et al. 2023). 본 시뮬레이션 연구 내용을 바탕으로 향후 양방향 측정치와 결합하여 궤도 결정 기능을 확장할 수 있을 것으로 생각한다. 또한 달 지상 사용자의 위치 결정 성능 평가에도 향후에는 활용할 수 있을 것으로 기대한다.
This work was partly supported by the Institute of Information & Communications Technology Planning & Evaluation (IITP)-ITRC (Information Technology Research Center) grant funded by the Korea government (MSIT) (IITP-2025-RS-2024-00437494, 50%), and funding from Korea government (Korea AeroSpace Administration, KASA) (grant number RS-2022-NR067078, 25% and RS-2022-00165802, 25%).
All the authors have contributed to the presented work. The first author, S.K. wrote and edited this based on the analysis results. J.O. performed verification of the analysis algorithm and confirmed the results. B.P. suggested the original concept of this research and supervised the direction of the research. H.P. and J-M.J have administered the project.
The authors declare no conflict of interest.
Anghileri, M., Paonni, M., Fontanella, D., & Eissfeller, B. 2013, GNSS Data Message Performance: A New Methodology for its Understanding and Ideas for its Improvement, In 2013 International Technical Meeting of The Institute of Navigation, San Diego, California, 28-30 January 2013, pp.638-650. https://www.ion.org/publications/abstract.cfm?articleID=10839
ASI 2025, LuGRE sets another record: first GNSS signals detected in lunar orbit [internet], cited 2025 Aug 8, available from: https://www.asi.it/en/2025/02/lugre-sets-another-record-first-gnss-signals-detected-in-lunar-orbit/
Bhattarai, S. 2015, Satellite clock time offset prediction in global navigation satellite systems, Doctoral dissertation, University College London.
Cabinet Office 2023, QZSS Antenna Patterns [Internet], cited 2025 Aug 8, available from: https://qzss.go.jp/en/technical/antenna-patterns.html
Capuano, V., Basile, F., Botteron, C., & Farine, P. A. 2016, GNSS-based Orbital Filter for Earth Moon Transfer Orbits, The Journal of Navigation, 69, 745-764. https://doi.org/10.1017/S0373463315000843
CSNO 2019, BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B1I (Version 3.0) [Internet], cited 2025 Aug 8, available from: http://en.beidou.gov.cn/SYSTEMS/ICD/201902/P020190227702348791891.pdf
Dafesh, P. A., Wong, N., Khadge, G. K., Djuknic, G., Crenshaw, J., et al. 2025, The Design of a Flexible, Interoperable Navigation Signal for Future Lunar Missions, In Proceedings of the 2025 International Technical Meeting of The Institute of Navigation, Long Beach, California, 27-30 January 2025, pp.712-731. https://doi.org/10.33012/2025.19961
Delépaut, A., Giordano, P., Ventura-Traveset, J., Blonski, D., Schönfeldt, M., et al. 2020, Use of GNSS for lunar missions and plans for lunar in-orbit development, Advances in Space Research, 66, 2739-2756. https://doi.org/10.1016/j.asr.2020.05.018
Delépaut, A., Minetto, A., Dovis, F., Melman, F., Giordano, P., et al. 2022, Enhanced GNSS-based Positioning in space exploiting Inter-Spacecraft Cooperation, in 2022 International Technical Meeting of The Institute of Navigation, Long Beach, California, 25-27 January 2022, pp.530-544. https://doi.org/10.33012/2022.18214
Donaldson, J. E., Parker, J. J., Moreau, M. C., Highsmith, D. E., & Martzen, P. D. 2020, Characterization of on-orbit GPS transmit antenna patterns for space users, NAVIGATION: Journal of the Institute of Navigation, 67, 411-438. https://doi.org/10.1002/navi.361
Giordano, P., Grenier, A., Zoccarato, P., Bucci, L., Cropp, A., et al. 2021a, Moonlight navigation service – how to land on peaks of eternal light. In 72nd international astronautical congress, Dubai, United Arab Emirates, 25-29 October 2021.
Giordano, P., Grenier, A., Zoccarato, P., Swinden, R., Trenta, D., et al. 2021b, Orbit determination and time synchronisation in lunar orbit with GNSS – Lunar Pathfinder experiment, In 72nd international astronautical congress, Dubai, United Arab Emirates, 25-29 October 2021.
Giordano, P., Swinden, R., Gramling, C., Crenshaw, J., & Ventura-Traveset, J. 2023, LunaNet Position, Navigation, and Timing Services and Signals, Enabling the Future of Lunar Exploration, in 36th International Technical Meeting of the Satellite Division of The Institute of Navigation, Denver, Colorado, 11-15 September 2023, pp.3577-3588. https://doi.org/10.33012/2023.19345
Hrbek, S. J., Won, D. H., & Akos, D. M. 2016, Power Characterization for L1 and L5 Transmissions, In Proceedings of the 2016 International Technical Meeting of The Institute of Navigation, Monterey, California, 25-28, January 2016, pp.873-880. https://doi.org/10.33012/2016.13468
Iiyama, K., Vila, G. C., & Gao, G. 2023, LuPNT: Open-Source Simulator for Lunar Positioning, Navigation, and Timing, In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), Denver, Colorado, 11-15 September 2023, pp.1499-1510. https://doi.org/10.33012/2023.19373
ISECG 2024, GLOBAL EXPLORATION ROADMAP [Internet], cited 2025 Aug 8, available from: https://www.globalspaceexploration.org/wp-content/isecg/GER2024.pdf
Israel, D. J., Mauldin, K. D., Roberts, C. J., Mitchell, J. W., Pulkkinen, A. A., et al. 2020, LunaNet: a Flexible and Extensible Lunar Exploration Communications and Navigation Infrastructure, In 2020 IEEE Aerospace Conference, Montana, USA, 07-14 March 2020, pp.1-14. https://doi.org/10.1109/AERO47225.2020.9172509
Jin, M., Choi, H., Kim, K., Park, C., Ahn, J., et al. 2012, The Design Method of GNSS Signal Using the Analysis Result of Receiver Performance, The Journal of Korean Institute of Communications and Information Sciences, 37, 502-511. https://doi.org/10.7840/KICS.2012.37.6C.502
Julien, O., Macabiau, C., & Bertrand, E. 2010, Analysis of Galileo E1 OS unbiased BOC/CBOC tracking techniques for mass market applications, In 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, Netherlands, 08-10 December 2010, pp.1-8. https://doi.org/10.1109/NAVITEC.2010.5708070
Kaplan, E. D., & Hegarty, C. 2017, Understanding GPS/GNSS: principles and applications. 3rd ed. (Boston: Artech house).
Kawade, P. & Christodoulopoulou, D. 2024, Lunar markets 4th edition [Internet], cited 2025 Aug 8, available from: https://www.analysysmason.com/research/content/reports/lunar-markets-nsi015
Kim, K., Jo, Y., Park, B., & Kim, O.-J. 2024a, An Experimental Investigation on Broadcast Intervals and Sequences of GPS CNAV, QZSS LNAV/CNAV, and BDS CNAV/CNAV-2, Journal of Positioning, Navigation, and Timing, 13, 319-329. https://doi.org/10.11003/JPNT.2024.13.3.319
Kim, S., Lee, Y., Jo, Y., Cha, Y., Park, B., et al. 2024b, Analysis of Spatial Correlation and Linear Modeling of GNSS Error Components in South Korea. Journal of Positioning, Navigation, and Timing, 13, 221–235. https://doi.org/10.11003/JPNT.2024.13.3.221
Long, A. C. & Stacey, N. 2025, Goddard Enhanced Onboard Navigation System (GEONS) 3.1 Mathematical Specifications, NASA Goddard Space Flight Center Technical Report, NASA/TP-20250006484
Marquis, W. A. & Reigh, D. L. 2015, The GPS Block IIR and IIR-M Broadcast L-band Antenna Panel: Its Pattern and Performance, NAVIGATION: Journal of the Institute of Navigation, 62, 329-347. https://doi.org/10.1002/navi.123
Menzione, F., Sgammini, M., & Paonni, M. 2024, Reconstruction of Galileo Constellation Antenna Pattern for Space Service Volume Applications, Publications Office of the European Union Technical Report, JRC135110. https://doi.org/doi:10.2760/765842
Montenbruck, O., Schmid, R., Mercier, F., Steigenberger, P., Noll, C., et al. 2015, GNSS satellite geometry and attitude models, Advances in Space Research, 56, 1015-1029. https://doi.org/10.1016/j.asr.2015.06.019
Montenbruck, O., Steigenberger, P., & Hauschild, A. 2018, Multi-GNSS signal-in-space range error assessment – Methodology and results, Advances in Space Research, 61, 3020-3038. https://doi.org/10.1016/j.asr.2018.03.041
Murata, M., Akiyama, K., & Naoki, S. 2024, Lunar Navigation Satellite System for Entire Moon Surface: HDOP and SISE Evaluation, In 2024 International Technical Meeting of The Institute of Navigation, Long Beach, California, January 23-25 2024, pp.778-786. https://doi.org/10.33012/2024.19495
Nakajima, Y. & Yamamoto, T. 2024, Enhancing Navigation Accuracy in a Geostationary Orbit by Utilizing a Regional Navigation Satellite System, NAVIGATION: Journal of the Institute of Navigation, 71. https://doi.org/10.33012/navi.641
Navigation Center 2022, GPS Technical References [Internet], cited 2025 Aug 8, available from: https://www.navcen.uscg.gov/gps-technical-references
Noh, J. H., Jo, G. H., Lee, J. Y., & Lee, S. J. 2022, Performance Analysis of GNSS Navigation Messages in the Structure Viewpoint, Journal of Positioning, Navigation, and Timing, 11, 135-146. https://doi.org/10.11003/JPNT.2022.11.2.135
Parker, J. J., Dovis, F., Anderson, B., Ansalone, L., Ashman, B., et al. 2022, The Lunar GNSS Receiver Experiment (LuGRE), In 2022 International Technical Meeting of The Institute of Navigation, Long Beach, California, 25-27 January 2022, pp.420-437. https://doi.org/10.33012/2022.18199
Popescu, O. 2017, Power Budgets for CubeSat Radios to Support Ground Communications and Inter-Satellite Links, IEEE Access, 5, 12618-12625. https://doi.org/10.1109/ACCESS.2017.2721948
SAIC 2022, Navstar GPS Space Segment/ User Segment L5 Interfaces (IS-GPS-705J) [Internet], cited 2025 Aug 8, available from: https://www.gps.gov/technical/icwg/IS-GPS-705J.pdf
Teunissen, P. J. & Montenbruck, O. 2017, Springer Handbook of Global Navigation Satellite Systems (Cham: Springer International Publishing).
United Nations Office for Outer Space Affairs 2021, The Interoperable Global Navigation Satellite Systems Space Service Volume Second Edition [Internet], cited 2025 Aug 8, available from: https://www.unoosa.org/res/oosadoc/data/documents/2021/stspace/stspace75rev_1_0_html/st_space_75rev01E.pdf
Wang, M., Shan, T., Liu, L., Huan, H., & Tao, R. 2022, On-orbit BDS signals and transmit antenna gain analysis for a geostationary satellite, Advances in Space Research, 69, 2711-2723. https://doi.org/10.1016/j.asr.2022.01.022
Wang, T., Ruf, C., Block, B., McKague, D., & Gleason, S. 2018, Characterization of GPS L1 EIRP: Transmit Power and Antenna Gasin Pattern, In 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, Florida, 24-28 September 2018, pp.2879-2890. https://doi.org/10.33012/2018.16101
Williams, J., Lee, D. E., Whitley, R. J., Bokelmann, K. A., Davis, D. C., et al. 2017, Targeting Cislunar Near Rectilinear Halo Orbits for Human Space Exploration. In AAS/AIAA Space Flight Mechanics Meeting, San Antonio, Texas, 5-9 February 2017.
Winternitz, L. B., Bamford, W. A., Long, A. C., & Hassouneh, M. 2019, GPS Based Autonomous Navigation Study for the Lunar Gateway, In Annual American Astronautical Society (AAS) Guidance, Navigation, and Control Conference, Breckenridge, Colorado, 1-6 February 2019.