Department of Electronic Engineering, Hanyang University, Seoul 04763, South Korea
†Corresponding Author: Sunwoo Kim, E-mail: remero@hanyang.ac.kr
Citation: Seo, H., Jung, H., Yang, D., & Kim, S. 2025, GNN-based Localization with Beam RSRP in 5G Systems, Journal of Positioning, Navigation, and Timing, 14, 259-264.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 259-264. https://doi.org/10.11003/JPNT.2025.14.3.259
Received on Aug 12, 2025, Revised on Aug 23, 2025, Accepted on Aug 29, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In this study, we propose a Graph Neural Network (GNN)-based localization approach utilizing beam Reference Signal Received Power (RSRP) measurements in 5G networks. Existing GNN-based localization approaches have mainly targeted indoor environments with dense Base Station (BS) deployments and are less effective in outdoor scenarios where the number of BSs is limited. To overcome this limitation, we construct an expanded graph extracted by features such as RSRP, angle, and Line of Sight/None-Line of Sight (LoS/NLoS) indicators, assuming that such information is available at the User Equipment (UE). We validate the proposed approach through ray-tracing simulations in a realistic outdoor 5G environment and evaluate its localization accuracy compared to the triangulation approach.
5G localization, outdoor localization, beam RSRP, GNN, AI-based localization
최근 위치 정보는 산업 자동화, 자율주행, 긴급 구조와 같이 다양한 분야에서 활용되며, 높은 정밀도의 측위 기술은 서비스 품질을 보장하기 위해 필수적이다 (Laoudias et al. 2018). 기존의 실외 환경에서는 Global Navigation Service System (GNSS) 기반의 측위 기술이 핵심적인 기술로 사용되어 왔으며, 자동차 네비게이션 등 다양한 위치 기반 서비스에 효과적으로 적용되어 왔다. 그러나 GNSS 기반의 측위 기술은 도심의 고층 건물 밀집 지역과 같이 위성과의 Line of Sight (LoS)가 보장되지 않는 환경에서는 성능이 현저히 저하되는 한계가 존재한다. 이러한 문제를 해결하기 위하여 무선 통신 신호를 이용한 측위 기술이 대안으로 주목받고 있으며, 특히 5G 이동통신 기술의 발전과 함께 그 중요성이 더욱 부각되고 있다 (Mogyorósi et al. 2022). 이에 따라 무선 이동통신 국제 표준화 단체 3rd Generation Partnership Project (3GPP)에서는 5G New Radio (NR) 규격에 측위를 위한 전용 신호를 새롭게 도입하였으며, 3GPP Release 16에서는 시행 횟수의 80%에 대하여 실외 환경에서 수평 10 m, 수직 3 m 이내의 높은 측위 정확도를 요구하고 있다 (3GPP 2019).
하지만, 무선 통신 환경에서는 장애물에 의하여 신호가 차단되거나 반사되는 Non-Line of Sight (NLoS) 특징으로 인해 Time of Arrival (ToA), Angle of Arrival (AoA)과 같은 측위에 활용되는 측정값 에러가 크게 증가하여 측위 성능이 크게 저하되는 문제점이 있다 (Kirmaz et al. 2023). 이러한 무선 통신 신호 환경을 효과적으로 모델링하기 위해 최근에는 데이터 기반의 Artificial Intelligence (AI) 기법을 적용한 연구가 활발히 진행되고 있으며, 대표적인 사례로는 Convolutional Neural Network (CNN)와 Multi-Layer Perceptron (MLP)을 기반으로 한 무선 통신 측위 기법이 다수 제안되었다. 그러나 이러한 기존 AI 기법들은 무선 통신 환경의 특성을 충분히 반영하지 못하는 근본적인 한계를 지닌다. 예를 들어, CNN의 경우 격자 형태로 구조화된 데이터를 유클리드 공간에서 처리하는 것에 특화되어 있어 NLoS 및 다중 경로의 영향으로 송수신기 간의 관계가 단순한 거리 기반으로 표현되기 어려운 비유클리드적 공간 구조에서는 적합하지 않다. 또한 MLP는 입력 특징들을 독립적으로 처리하기 때문에 무선 채널에서 발생하는 송수신기 간의 복잡한 공간적 관계에 대한 효과적인 학습이 어렵다 (Shen et al. 2023).
이러한 기존 AI 기법들의 한계를 극복하고, 무선 통신 환경의 비유클리드 공간적 특성을 보다 정밀히 모델링하기 위한 대안으로 최근에는 Graph Neural Network (GNN) 기반의 측위 연구가 등장하였다. 그래프 기반의 모델링 기법은 데이터의 형태가 유클리드 공간에 국한되지 않고, 그래프를 구성하는 노드들의 연결 관계를 엣지로 표현하여 송수신기 간의 기하학적 관계와 네트워크 토폴로지를 현실적으로 반영할 수 있다는 장점을 갖는다 (Kipf & Welling 2017, Wu et al. 2020). 이러한 GNN의 구조적 강점을 활용한 무선 통신 기반 측위 연구가 활발히 이루어지고 있다. 예를 들어, Wang et al. (2024)과 Zhang et al. (2025)은 WiFi 신호를 기반으로 복잡한 실내 환경에서도 높은 정확도와 WiFi 기반의 적은 비용으로 효율성을 갖는 위치 추정이 가능함을 입증하였다. 이러한 실내 환경에서는 수십에서 수백 개의 Base Station (BS)을 그래프의 노드로 설정함으로써 노드 간 message passing을 기반으로 학습하는 GNN에 적합한 그래프를 구성하여 높은 위치 추정 정확도를 보일 수 있다. Liang & Meyer (2021), Jung et al. (2024, 2025)의 연구는 BS의 수가 제한되는 상황임에도 다중 단말을 노드로 추가하여 BS 및 다중 단말 간의 협력을 활용한 높은 위치 추정 정확도를 보였다.
그러나 실외 환경에서는 3GPP 38.901 (2025)에서 정의한 바와 같이 Urban Macro cell (UMa)의 셀 간 간격은 500 m, Urban Micro cell (UMi)의 셀 간 간격은 200 m에 이르며, 수십에서 수백 개의 BS가 밀집되는 실내 환경에 비하여 드문 간격의 BS 배치를 보인다. 이러한 특성은 실내 환경에서 가능했던 다수의 BS를 활용한 그래프 구성을 실외 환경에 적용하기에 현실적으로 불가능하게 만든다 . 또한 단말 간의 협력 정보를 이용한 측위는 참여하는 다중 단말 간의 동기화 수준에 의해 성능이 크게 좌우되며, 단말 간 측정 정보 공유 과정에서 프라이버시 침해 및 보안 위협이 발생할 수 있다 (Şahin et al. 2023, Yu et al. 2023). 이와 같은 요인들로 인하여 BS의 수가 제한된 실외 환경에서 단일 단말을 이용한 위치 추정은 적은 수의 노드를 갖게 되며, 이는 message passing 기반의 GNN 학습 구조에 적합하지 않은 그래프를 조성한다 (Jung et al. 2025). 또한 노드 간의 연결성이 부족할 경우 GNN이 송수신기 간의 공간적 관계나 무선 통신 환경의 전역적인 환경 정보를 학습하지 못하여 측위 성능이 크게 저하될 수 있다. 따라서 실외의 제한된 BS 환경에서도 무선 통신 신호에 내재된 공간적 특성을 효과적으로 표현하고 활용할 수 있는 새로운 그래프 구조 모델링 기법의 개발이 필수적이다.
이에 따라 본 논문에서는 5G 네트워크의 multi-beam 특성을 활용하여, 실외 환경에서의 BS 수 제한 문제를 해결할 수 있는 새로운 GNN 기반 측위 기법을 제안한다. 제안 기법의 핵심은 beam Reference Signal Received Power (RSRP) 측정값에 포함된 각도 정보 및 NLoS 경로 특성을 그래프 노드의 feature로 활용함으로써 그래프의 규모를 확장하고, 이를 통해 실외 환경에서 BS 수 제약을 극복하는 데 있다. 단말과 beam 간의 LoS/NLoS 관계를 기반으로 그래프의 엣지를 구성하여 공간적 연관성을 모델링하고, Graph Attention Network (GAT)를 적용하여 각 노드의 특징 벡터를 이웃 노드로부터 전달받은 정보를 이용해 갱신함으로써 LoS 환경에서의 주요 beam 정보에 높은 중요도가 반영되도록 한다 (Veličković et al. 2018). 특히, attention 메커니즘을 통해 이웃 노드의 중요도를 학습 과정에서 동적으로 반영함으로써, 환경 변화나 NLoS 환경에서도 강건성을 확보한다. 이러한 GAT의 구조적 특성은 각 beam의 기여도를 적응적으로 반영하여 측위 정확도를 향상시키는 중요한 역할을 한다. 이를 통해 제한된 수의 BS 환경에서도 충분한 그래프 복잡성을 확보함으로써 높은 측위 정확도를 달성할 수 있다. 마지막으로 실제 환경을 반영한 무선 채널 모델을 기반의 시뮬레이션을 통해 제안 기법의 성능을 정량적으로 분석하고 우수성을 입증한다.
서론에 이어 2장에서는 시스템 모델에 대해 서술하고 3장에서는 beam ID를 활용한 그래프 구성과 GAT 기반 측위 기법에 대해 서술한다. 4장에서 시뮬레이션 환경과 측위 결과 및 분석에 대해 서술하고 5장에서는 결론을 맺는다.
본 논문에서는 Fig. 1과 같은 시나리오를 따르며, 5G의 Orthogonal Frequency Division Multiplexing (OFDM) 기반 Multiple Input Multiple Output (MIMO) 시스템을 고려하여 총 $N_{tx}$개의 송신 안테나와 $N_{rx}$개의 수신 안테나를 사용하는 구조를 가정한다. 시간 슬롯 기반의 블록 페이딩 채널을 적용하여 각 OFDM 심볼 내에서 채널 응답이 고정되며, 최대 지연은 cyclic prefix의 길이 $T_{cp}$이내로 제한된다. 이때, 심볼 시간 $T_s$ 간격으로 샘플링된 이산 시간 $t=1,2,\ldots,T$에서 수신된 신호 $\mathbf{r}_t \in \mathbb{C}^{N_{\mathrm{rx}}\times 1}$는 Eq. (1)과 같이 표현된다.
$$\mathbf{r}_{t}
=
\sum_{\tau = 0}^{T_{cp}}
\mathbf{H}_{\tau}\, \mathbf{y}_{t-\tau}
+
\mathbf{N}_{t}$$
여기서 $\mathbf{H}_{\tau} \in \mathbb{C}^{N_{rx} \times N_{tx}}$는 베이스밴드 MIMO 채널에서 신호가 수신기에 도달하는 다양한 경로들을 표현하는 단위인 $\tau$-th tap에 대한 행렬이며, $\mathbf{y}_t \in \mathbb{C}^{N_{tx} \times 1}$는 송신 신호, $\mathbf{N}_t \in \mathbb{C}^{N_{rx} \times 1}$는 가우시안 백색 잡음으로 가정한다.
일반적인 OFDM 심볼 시간 내에서 MIMO 채널 $\mathbf{H}_{\tau}$은 여러 경로로 구성된 모델로 표현될 수 있으며, 각각의 경로 $ p = 1, 2, \ldots, P $는 Eq. (2)와 같이 모델링 된다.
$$\mathbf{H}_{\tau}
=
\sum_{p=0}^{P}
m_{p}\,
\mathbf{a}_{rx}\!\left(\phi_{rx,p},\, \psi_{rx,p}\right)\,
\mathbf{a}_{tx}^{\top}\!\left(\phi_{tx,p},\, \psi_{tx,p}\right)\,
g\!\left(\tau – \tau_{p}\right)$$
각 경로는 다음과 같은 요소들로 정의된다. 먼저, 복소 페이딩 계수 $m_p$는 해당 경로의 세기를 나타내며, 송신 안테나 어레이 응답 $\mathbf{a}_{tx}(\cdot) \in \mathbb{C}^{N_{tx} \times 1}$은 Angle of Departure (AoD)인 방위각 $\phi_{tx, p}$ 및 고도각 $\psi_{tx, p}$에 따른 송신 방향성을 나타낸다. 마찬가지로 수신 안테나 어레이 응답 $\mathbf{a}_{rx}(\cdot) \in \mathbb{C}^{N_{rx} \times 1}$은 AoA인 방위각 $\phi_{rx, p}$ 및 고도각 $\psi_{rx, p}$에 따라 수신 방향성이 정의된다. 신호는 각 경로 지연 $\tau_p$만큼 지연된 펄스 파형 $g(\cdot)$과 함께 전달되며, 모든 경로의 지연은 $\max(\tau_p) \le T_{cp}$를 만족한다고 가정한다 (Italiano et al. 2024).
본 연구에서는 측위를 위한 beam 별 RSRP 측정을 위해, 3GPP 표준에서 정의된 Positioning Reference Signal (PRS)을 활용한다. 앞서 정의한 OFDM 기반 MIMO 수신 신호 모델에 따라, 단말은 시간 t에서 수신된 신호 $\mathbf{r}_t$ 중 PRS가 할당된 자원 요소에 대해 각 beam의 수신 전력을 계산한다. BS는 초기 beam 설정 단계에서 선택된 넓은 각도 범위 내에서 보다 정밀한 송신 beam으로 PRS를 전송하고, 단말은 고정된 수신 beam을 통해 이를 신호를 수신한다. 이후 단말은 각 방향에 대해 수신된 PRS 심볼의 평균 전력을 계산하여 $m=1,2,\ldots,M$개 BS에 대해 $n=1,2,\ldots,N$개의 PRS beam RSRP 값 $ρ_m^{(n)}$을 추정한다. 해당 값은 수신 복소 신호의 절댓값 제곱을 모든 안테나에 대해 합산한 후 평균한 값으로 Eq. (3)과 같이 계산할 수 있다.
$$\rho_{m}^{(n)}
=
\frac{1}{S}
\sum_{s=1}^{S}
\left\lVert
\mathbf{c}_{s}^{(m,n)} \,
\right\rVert^{2}$$
여기서 $\mathbf{c}_{s}^{(m,n)} \in \mathbb{C}^{N_{rx} \times 1}$은 수신 신호 $\mathbf{r}_t$ 중 PRS가 할당된 $m$번째 BS의 $n$번째 beam 방향의 복소수 샘플이며, $S$는 해당 beam 방향에 대해 수신된 총 PRS 심볼의 수를 의미한다.
Beam RSRP를 포함한 $m$번째 BS의 $n$번째 beam에서 얻어지는 측정값 벡터 $\mathbf{z}_{m}^{(n)} \in \mathbb{R}^{1 \times 4}$은 Eq. (4)와 같다.
$$\mathbf{z}_{m}^{(n)}
=
\left[
\, b_{m},\;
c_{m},\;
l_{m},\;
\rho_{m}^{(n)}
\right]$$
여기서 $b_m$은 BS의 인덱스, $c_m$은 단말과 연결된 BS cell의 인덱스이며, $l_m$은 해당 BS와 단말 간의 LoS/NLoS 상태를 나타내는 지표이다. 측정값 벡터 $\mathbf{z}_m^{(n)}$는 $m$번째 BS에 대해 행렬 $\mathbf{Z}_{m} \in \mathbb{R}^{N \times 4}$로 나타낸다.
$$\mathbf{Z}_m
=
\left[
\, \mathbf{z}_m^{(1)},\; \ldots,\; \mathbf{z}_m^{(N)}
\right]^{\top}$$
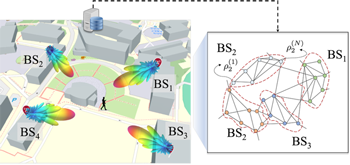
Fig. 1. The 5G MIMO scenario in an outdoor environment, with a graph representation.
BS의 beam과 단말 사이의 무선 통신 환경을 그래프 $g=(V,E)$ 형태로 모델링한다. 여기서 집합 $V=(v_1,\ldots,v_I)$는 BS에 속하는 beam으로 구성되는 총 i = {1,2, … ,I}개 노드의 집합이며, 각 노드는 Eq. (4)와 같은 측정값 벡터를 노드의 특징으로 갖는다. 집합 E는 노드 간의 연결성을 나타내는 엣지의 집합이다. 노드 간의 연결성은 무선 신호의 전파 특성을 반영하여 차별적으로 설정된다. LoS 환경에서는 BS와 단말이 직접적인 신호 전달이 가능하므로 노드 간 강한 연관성을 가정하여 노드 $i,j$에 대하여 $e_{i,j}=1$로 연결성을 부여하는 반면, 장애물로 인한 신호 감쇠와 다중 경로 전파가 존재하는 NLoS 환경에서는 $e_{i,j}=0$으로 노드 간의 연관성을 제거한다.
각 BS의 beam으로 구성된 초기의 노드 특징 행렬 $\mathbf{H}^{(0)} \in \mathbb{R}^{(M \times N)\times 4}$는 Eq. (6)과 같이 구성된다.
$$\mathbf{H}^{(0)}
=
\left[
\mathbf{Z}_{1},\; \ldots,\; \mathbf{Z}_{M}
\right]^{\top}$$
여기서, GAT 기반 측위 모델의 입력으로 주어지는 노드의 초기 특징은 각 BS의 beam에 대한 측정값 벡터 $\mathbf{z}_m^{(n)}$을 결합하여 구성된다. 따라서, 총 $I=M \times N$개 노드에 대해 $\mathbf{H}^{(0)} = [\, \mathbf{h}_1^{(0)},\, \mathbf{h}_2^{(0)},\, \ldots,\, \mathbf{h}_I^{(0)} \,]^{\top}$, $\mathbf{h}_i^{(0)} \in \mathbb{R}^{1 \times 4}$와 같이 정의된다.
앞서 서술한 바와 같이, 그래프를 기반으로 모델링 된 무선 통신 환경에서의 측위를 위해 GAT 모델을 사용한다. GAT는 이웃 노드의 상대적 중요도를 동적으로 조정함으로써, 다양한 환경에서도 위치 추정의 강건성을 보일 수 있다. 노드 $i$에 대한 $j$의 중요도를 나타내는 attention 계수 $\alpha_{i,j}$는 Eq. (7)과 같이 구할 수 있다.
$$\alpha_{i,j}
=
\frac{
\exp\!\left(
\mathrm{LeakyReLU}\!\left(
\mathbf{v}^{\top}
\left[
\mathbf{Wh}_i \,\|\, \mathbf{Wh}_j
\right]
\right)
\right)
}{
\displaystyle
\sum_{j,k \in \mathcal{N}(i)}
\exp\!\left(
\mathrm{LeakyReLU}\!\left(
\mathbf{v}^{\top}
\left[
\mathbf{Wh}_i \,\|\, \mathbf{Wh}_k
\right]
\right)
\right)
}$$
여기서, $\mathbf{v} \in \mathbb{R}^{2(k+1)}$는 attention score 생성을 위한 가중치 벡터로 $f$는 k = {0,1, … ,K}번째 레이어의 노드 특징의 차원을 나타낸다. $\mathbf{W} \in \mathbb{R}^{(f+1)\times f}$는 각 노드의 특징을 고차원으로 표현하기 위한 학습 가능한 가중치 행렬이며, $N(i)$는 노드 $i$의 이웃 노드를 의미한다. LeakyReLU는 음수 영역에 기울기 $\alpha=0.2$를 갖는 비선형 함수이며, $\Vert$는 concatenation 연산을 의미한다.
GAT의 $k$번째 레이어에서의 노드 특징 $\mathbf{h}_i^{(k)}$은 Eq. (8)과 같이 이웃 노드 간의 정보를 가중치를 이용하여 갱신된다.
$$\mathbf{h}_i^{(k)}
=
\sigma\!\left(
\sum_{j \in N(i)}
\alpha_{i,j}\,
\mathbf{W}^{(k)}
\, \mathbf{h}_j^{(k-1)}
\right)$$
여기서 $\sigma$는 activation function이며, 주로 ReLU, Leaky ReLU가 사용된다.
최종 $K$번째 레이어를 통과한 후 얻어진 노드 임베딩 $\mathbf{h}_i^{(K)}$는 위치 추정을 위한 입력으로 사용된다. 이를 MLP에 입력하여 단말의 추정 위치 $\hat{\mathbf{u}}$를 Eq. (9)와 같이 계산한다.
$$\hat{\mathbf{u}}
=
\mathrm{MLP}\!\left( \mathbf{h}_i^{(K)} \right)$$
이후 모델은 추정된 위치 $\hat{\mathbf{u}}$와 실제 위치$\mathbf{u}$ 간의 평균 제곱 오차(Mean Squared Error, MSE)를 최소화하도록 학습된다.
본 논문에서는 한양대학교 캠퍼스를 배경으로 5G 기반 측위 시뮬레이션을 수행하였다. 시뮬레이션 환경은 MATLAB의 ray-tracing을 활용하였으며, 총 4개의 BS를 약 133 m × 133 m 크기의 환경에 배치하였다. 각 BS당 3개의 cell을 구성하여, 총 12개의 cell이 단말을 중심으로 다양한 방향에서 신호를 송수신할 수 있도록 설정하였다. 각 BS는 8×8 Uniform Planar Array (UPA) 구조의 송신 안테나 배열을 갖고, 단말은 2×2 안테나 배열을 적용하였다. 각 위치에서 하향링크 PRS 신호의 beam RSRP를 측정하여 측위에 사용하였으며, 채널 모델은 2차 반사를 포함하는 Shooting and Bouncing Rays (SBR) 기반으로 구성하여 NLoS에서도 다중 경로 특성을 반영하였다. GAT 기반 위치 추정 모델의 구성은 Fig. 2와 같다. 여기서의 b는 배치 사이즈, N는 그래프 노드의 크기이다.
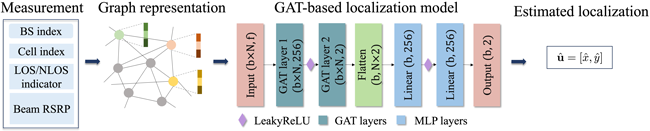
Fig. 2. Architecture of the proposed GAT-based localization approach.
본 논문에서는 상기 시뮬레이션 환경을 기반으로, GNN 구조를 활용하여 단말 위치 추정 성능을 다양한 조건에서 정량적으로 평가한다. 특히 제안하는 GAT 기반의 위치 추정 모델의 효과를 입증하기 위하여, 직접 경로 신호의 도착 시간인 ToA 기반의 삼변측량 측위 기법과의 비교 실험을 수행한다. 이를 통하여 GNN이 무선 채널에서의 공간적 관계와 신호 세기 정보를 얼마나 효과적으로 학습하고 활용할 수 있는지를 분석한다. 실험에서는 동일한 PRS 기반 시뮬레이션 데이터를 활용하되, 각 모델에 맞는 입력 형식으로 변환하여 학습 및 평가를 진행하며, 예측된 위치와 실제 위치 간의 평균 제곱 오차와 누적 분포 함수(Cumulative Distribution Function, CDF)를 기반으로 정확도를 측정한다.
첫번째로, GAT 기반 위치 추정 기법과 전통적인 ToA 기반 삼변측량 위치 추정 기법의 성능 차이를 분석하기 위한 시뮬레이션을 진행하였으며 이를 통해 얻어진 위치 추정 오차의 누적 CDF를 Fig. 3에 나타낸다. Fig. 3에 따르면 CDF 80%를 기준으로 보았을 때 GAT 기반 기법은 약 7.68 m의 성능을 보이는 반면, ToA 기반 삼변측량 기법은 약 85.32 m의 위치 추정 오차가 발생하는 등 전체적으로 낮은 추정 성능을 보였다. Fig. 4는 각 BS로부터 측정된 ToA의 거리 오차를 분석한 결과이며 2, 4번 BS에서 상당히 큰 거리 오차를 볼 수 있다. 이러한 특정 BS에서의 상당한 거리 추정 오차가 누적되어 전체 ToA 기반 삼변측량 기법 성능 저하의 주요 원인으로 작용되었다. 이는 본 시뮬레이션 환경이 NLoS 및 다중 경로 특성이 복합적으로 존재하는 복잡한 외부 환경임을 반영하여 ToA 기반 삼변측량 기법이 이러한 NLoS 환경에서 오차에 민감하다는 기존 연구의 결과와도 일치한다. 반면, GAT는 beam 별 공간 정보와 관계를 학습하여 노드 간 유사성을 기반으로 비선형적인 공간 구조를 파악할 수 있으므로, 복잡한 채널 조건에서도 안정적인 위치 추정이 가능함을 수치적으로 증명하였다.
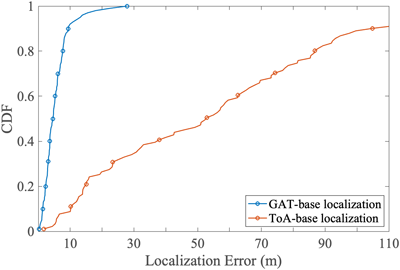
Fig. 3. CDF of localization error for proposed vs. triangulation.
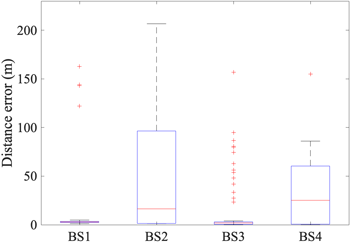
Fig. 4. ToA measurement error between the actual ToA and the measured ToA for each BS in Ray-tracing.
두번째로는 beam 수의 변화에 따른 GAT 기반 위치 추정 성능의 민감도를 확인하기 위해 동일한 학습 조건 하에 입력되는 beam RSRP 수를 64개와 12개로 구성하여 실험을 수행하였고 위치 추정 오차의 CDF를 Fig. 5에 나타내었다. CDF의 80% 지점에서 64개 beam 사용 시 위치 오차는 약 7.68 m, 12개 beam 사용 시 약 15.1 m로 약 49.13%의 성능 향상이 있었으며, CDF의 50% 지점에서도 각각 4.67 m, 8.83 m로 약 48.24% 오차 차이를 보였다. 이러한 성능 차이는 beam 수가 증가함에 따라 그래프 내 노드 수가 증가하고, 각 노드는 세밀한 방향성 정보를 가지게 되어 보다 풍부한 공간 정보를 제공하게 된다. 결과적으로 GAT의 message passing 과정에서 노드 간의 유의미한 관계성이 보다 명확히 학습되고, attention 기반의 가중치 학습을 통해 위치 결정에 중요한 정보가 강조되므로 위치 추정 정확도가 향상된 것으로 판단된다. 다만 beam 수의 증가는 그래프 내 노드 수 확대로 이어지며, 이는 곧 message passing 과정에서 고려해야 할 엣지의 수도 함께 증가시킨다. 본 논문에서 사용한 GAT의 연산 시간 복잡도는 그래프의 엣지 수 $|\varepsilon|$에 비례하는 $O\bigl(|\varepsilon|\bigr)$로 표현되며, 이를 고려하였을 때 beam 수가 많아질수록 위치 추정 성능은 증가하지만 연산 복잡도가 커지는 trade-off가 발생한다 (Wu et al. 2020). 이러한 점은 성능 향상과 더불어 실시간 서비스 적용 가능성을 논의할 때 반드시 고려되어야 할 요소이다.
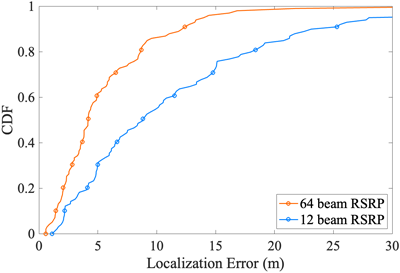
Fig. 5. Comparison of the proposed approach with different numbers of beam-RSRP.
본 논문에서는 실외 환경에서 BS 수가 제한된 상황에서도 효과적인 위치 추정을 가능하게 하는 GAT 기반 측위 기법을 제안하였다. 제안 기법은 5G 네트워크에서 수신되는 beam RSRP LoS/NLoS 정보 등을 노드 feature로 활용하고, 단말과 beam의 공간적 관계를 기반으로 그래프를 구성한 후, GAT를 적용하여 중요한 beam 정보에 가중치를 부여함으로써 단말의 위치를 추정하였다. 시뮬레이션을 통하여 GAT 기반 위치 추정 기법이 기존의 ToA 기반 삼변측량 기법에 비해 NLoS 환경에서 우수한 성능을 보임을 확인하였고, beam 수 확장을 통해 공간 정보의 세밀함이 증가할수록 위치 추정 정확도가 향상됨을 수치적으로 검증하였다. 하지만, beam 수에 따라 그래프의 노드 수 및 엣지의 수가 증가하고 이는 GAT의 연산 시간 복잡도를 증가시키므로 실시간 위치 추정 서비스에 적용하기 위해서는 성능 향상과 연산 부담 간의 균형을 고려한 beam 수 선택이 중요하다. 향후에는 다양한 환경 조건과 시간 변화에 따른 단말 이동성까지 고려할 수 있는 확장된 GNN 기반 측위 기법에 대한 연구가 필요하다.
이 연구 성과는 정부(방위사업청)의 재원으로 미래도전국방기술과제를 통해 수행된 연구임 (No.915087201).
Conceptualization, H. Seo, H. Jung, and D. Yang; software, H. Seo, and H. Jung; validation, H. Seo, H. Jung, and D. Yang; formal analysis, H. Seo, H. Jung, D. Yang, and S. Kim; data curation H. Seo, H. Jung, D. Yang, and S. Kim; writing—original draft preparation, H. Seo; writing—review and editing, H. Seo, H. Jung, D. Yang, and S. Kim; visualization, H. Seo, H. Jung, D. Yang, and S. Kim; supervision, S. Kim; project administration, S. Kim; funding acquisition, S. Kim.
The authors declare no conflict of interest.
3GPP 2019, Study on NR positioning support, TR 38.855. https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3501
3GPP 2025, Study on channel model for frequencies from 0.5 to 100 GHz, TR 38.901. https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3317
Italiano, L., Tedeschini, B. C., Brambilla, M., Huang, H., Nicoli, M., et al. 2024, A Tutorial on 5G Positioning, IEEE Communications Surveys & Tutorials, 27, 1488-1535. https://doi.org/10.1109/COMST.2024.3449031
Jung, H., Jeong, M., Hameed, I., & Kim, S. 2024, GCN-based Cooperative Localization using Sidelink Communication in 3GPP Urban Environment, IEEE Vehicular Technology Conference, Washington DC, USA, 07-10 October 2024, pp.1-6. https://doi.org/10.1109/VTC2024-Fall63153.2024.10758057
Jung, H., Ko, S.-W., & Kim, S. 2025, Towards cooperative localization with implicit connectivity: graph neural network approach, IEEE Wireless Communications Letters, Early access, 1. https://doi.org/10.1109/LWC.2025.3588339
Kirmaz, A., Şahin, T., Michalopoulos, D. S., & Gerstacker, W. 2023, ToA and TDoA estimation using artificial neural networks for high-accuracy ranging, IEEE Journal on Selected Areas in Communications, 41, 3816-3830. https://doi.org/10.1109/JSAC.2023.3322803
Kipf, T. N. & Welling, M. 2017, Semi-supervised classification with graph convolutional networks (ICLR 2017), arXiv:1609.02907. https://doi.org/10.48550/arXiv.1609.02907
Laoudias, C., Moreira, A., Kim, S., Lee, S., Wirola, L., et al. 2018, A Survey of Enabling Technologies for Network Localization, Tracking, and Navigation, IEEE Communications Surveys & Tutorials, 20, 3607-3644. https://doi.org/10.1109/COMST.2018.2855063
Liang, M. & Meyer, F. 2021, Neural Enhanced Belief Propagation for Cooperative Localization, IEEE Statistical Signal Processing Workshop, Rio de Janeiro, Brazil, 11-14 July 2021, pp.326-330. https://doi.org/10.1109/SSP49050.2021.9513853
Mogyorósi, F., Revisnyei, P., Pašić, A., Papp, Z., Törös, I., et al. 2022, Positioning in 5G and 6G networks-a survey, Sensors, 22, 4757. https://doi.org/10.3390/s22134757
Şahin, T., Chiarello, L., Michalopoulos, D. S., & Panzner, B. 2023, Performance Evaluation of 5G Sidelink Positioning, IEEE Conference on Standards for Communications and Networking, Munich, Germany, 6-8 November 2023, pp.177-182. https://doi.org/10.1109/CSCN60443.2023.10453141
Shen, Y., Zhang, J., Song, S. H., & Letaief, K. B. 2023, Graph neural network for wireless communications: from theory to practice, IEEE Transactions on Wireless Communications, 22, 3554-3569. https://doi.org/10.1109/TWC.2022.3219840
Veličković, P., Cucurull, G., Casanova, A., Romero, A., Liò, P., et al. 2018, Graph attention networks, in Proc. of International Conference on Learning Representations, arXiv:1710.10903. https://doi.org/10.48550/arXiv.1710.10903
Wang, S., Zhang, S., Ma, J., & Dobre, O. A. 2024, Graph-neural-network-based WiFi indoor localization system with access point selection, IEEE Internet of Things Journal, 11, 33550-33564. https://doi.org/10.1109/JIOT.2024.3430087
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., et al. 2020, A Comprehensive Survey on Graph Neural Networks, IEEE Transactions on Neural Networks and Learning Systems, 32, 4-24. https://doi.org/10.1109/TNNLS.2020.2978386
Yu, D., Shi, X., Chai, L., Zhang, W., & Chen, J. 2023, Balancing Localization Accuracy and Location Privacy in Mobile Cooperative Localization, IEEE Transactions on Signal Processing, 71, 2804-2818. https://doi.org/10.1109/TSP.2023.3292505
Zhang, W., Shen, X., & Xia, S. 2025, GLoc: GNN in indoor localization, IEEE Internet of Things Journal, 12, 15090-15100. https://doi.org/10.1109/JIOT.2025.3529901