1Principal Researcher, Maritime R&D Center, LIG Nex1, Seongnam, Gyeonggi-do 13488, Korea
2Senior Researcher, Maritime R&D Center, LIG Nex1, Seongnam, Gyeonggi-do 13488, Korea
†Corresponding Author: Chul Hyun, E-mail: chul.hyun@gmail.com
Citation: Hyun, C., Kim, H., Kim, D. G., & Lee, S. 2025, GNSS-Synchronized Surface Buoy Network TDOA for Underwater Target Localization, Journal of Positioning, Navigation, and Timing, 14, 291-297.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 291-297. https://doi.org/10.11003/JPNT.2025.14.3.291
Received on Aug 14, 2025, Revised on Aug 21, 2025, Accepted on Aug 23, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Time Difference of Arrival (TDOA) localization using GNSS-synchronized surface buoys offers a promising solution for underwater emitter tracking without direct cable or acoustic links. However, the achievable localization accuracy depends on the interplay of buoy geometry, time-synchronization errors, and dynamic tracking constraints. This paper presents a quantitative analysis of these trade-offs using both static and dynamic scenarios. For static localization, Geometric Dilution of Precision (GDOP) and Root Mean Square Error (RMSE) are evaluated under varying buoy formations and clock errors. For dynamic tracking, an Extended Kalman Filter (EKF) framework incorporating realistic ping update rates is applied to evaluate track persistence and accuracy over time. Simulation results show that the buoy geometry strongly influences GDOP patterns and error sensitivity, time-synchronization errors above the millisecond scale rapidly degrade localization performance, and in dynamic tracking, slower ping rates combined with unfavorable geometries can cause error plateaus even when filtering is applied. These findings provide practical guidelines for designing GNSS-synchronized buoy networks by balancing geometry selection, synchronization precision, and update rate according to operational requirements.
GNSS synchronization, surface buoy network, time difference of arrival, underwater
수중에서 운용되는 자율무인잠수정(Autonomous Underwater Vehicle, AUV)은 해양 탐사, 군사 작전, 환경 모니터링 등 다양한 분야에서 활용되고 있다. 그러나 수중 환경에서는 전파가 급격히 감쇠되어 글로벌 위성항법시스템(Global Navigation Satellite System, GNSS)을 직접 수신할 수 없으므로, 정확한 위치 추정을 위해 별도의 항법·위치결정 기법이 요구된다. 전통적으로 사용되는 장거리측위(Long Baseline, LBL), 단거리측위 (Short Baseline, SBL), 초단거리측위(Ultra Short Baseline, USBL) 방식은 각각의 장점에도 불구하고 설치·운용 비용, 기준점 고정 설치에 따른 제약, 시야 제한 등 구조적 한계를 가진다 (Kilfoyle & Baggeroer 2000, Stojanovic & Preisig 2009, Paull et al. 2014).
이러한 한계를 극복하기 위해 GNSS 수신이 가능한 수상 플랫폼과 수중 음향 수신기를 결합하는 하이브리드 방식이 제안되어 왔다. 이 방식은 수상에서 고정밀 위치와 시간 기준을 확보한 뒤, 수중 표적과의 음향 신호 도달시간(Time of Arrival, TOA) 또는 도달시간차(Time Difference of Arrival, TDOA)를 계산하여 위치를 산출한다. GNSS 동기화 기반의 표면 노드 네트워크는 설치·회수의 편의성, 확장성, 시야 제약 완화 등의 장점이 있으며 (Han et al. 2015, Zhang et al. 2016), 특히 부이형 또는 소형 자율수상정(autonomous surface vehicle)을 활용할 경우 작전 환경에 맞춘 유연한 배치가 가능하다.
대표적인 관련 연구로 Otero et al. (2023)는 Global Positioning System (GPS)와 음향 모뎀을 결합한 표면 부이 네트워크를 제안하고, 부이 배치 기하와 채널 환경에 따른 성능 특성을 분석하였다. Aparicio et al. (2016)는 GPS 동기 표면 노드와 직접확산스펙트럼(direct sequence spread spectrum) 기반 양방향 음향 통신을 이용하여, 마스터 노드(예: 모선)에서 AUV 위치를 계산하는 방식을 제시하였다. 이러한 구조는 AUV가 부이 신호를 수신·응답하여 자율적으로 위치를 계산하거나 항로 계획을 갱신할 수 있다는 점에서 장점이 있다.
본 연구는 이에 비해 AUV가 단방향으로 송신하는 ping 신호를 다중 부이가 수신하고, 네트워크 상에서 TDOA를 계산한 뒤 중앙 처리 노드에서 위치를 추정하는 구조를 제안한다. 이 방식은 AUV 측의 하드웨어·연산 부담을 최소화하고, 부이 네트워크 확장성 및 멀티-AUV 지원 가능성을 높인다. 또한 운용 개념상, 외부에서 종합 위치 정보를 처리한 후 필요한 핵심 정보만 AUV에 재전송하거나 해상시험장에서 실시간 모니터링 용도로 활용하는 데 적합하다. GNSS 기반 동기화만 확보되면, 부이 간 RF 네트워크를 통해 실시간 위치 계산이 가능하므로, 운용 편의성과 비용 효율성 측면에서 이점을 가진다.
수중 위치결정의 정밀도는 부이 배치 기하학적 정밀도 희석(Geometry of Dilution of Precision, GDOP)과 시계 동기 오차( )에 크게 영향을 받으며, 여기에 표적의 속도와 위치 업데이트 주기 등이 복합적으로 작용한다 (Chan & Ho 1994, Zhang et al. 2016, Shaukat et al. 2021). 예를 들어 Shaukat et al. (2021)는 복수 센서와 필터 기반 융합기법을 통해 수중 플랫폼의 위치 정확도를 향상시킬 수 있음을 보였는데, 이는 본 연구에서 확장 칼만 필터(Extended Kalman Filter, EKF)를 활용하여 동적 추적 정밀도를 개선하는 접근과도 맥락을 같이 한다.
본 논문에서는 우선 정적 시나리오에서 부이 간격, 형상, $\sigma_t$ 조합에 따른 평균제곱근오차(Root Mean Square Error, RMSE) 변화를 시뮬레이션으로 분석하여 최적 배치 지침을 도출한다. 이어 동적 시나리오에서는 Loosely Coupled EKF를 적용하여 표적 속도($v$)와 ping 주기($T_{ping}$)의 조합이 추적 오차에 미치는 영향을 정량화한다. 분석 결과를 토대로, 위치 오차의 RMSE가 2 m 이하로 유지될 수 있는 $v$, $T_{ping}$, $\sigma_{t}$ 조합 범위를 제시하고, GNSS-denied 환경에서 실용적인 설계 가이드를 제공한다.
본 연구에서 제안하는 수중 위치 추적 시스템은 GNSS 동기 기반의 해상 부이 네트워크를 중심으로 구성된다. AUV는 자체적으로 위치 계산이나 시간 동기화를 수행하지 않고, 일정 주기로 수중 음향 ping 신호만 송신한다. 수면에 배치된 다수의 부이는 GNSS 수신기를 통해 실시간 절대 위치와 Pulse Per Second (PPS) 신호를 확보하여 공통 시간 기준을 유지하며, AUV로부터 송신된 ping 신호의 TOA를 측정한다. 각 부이는 측정된 TOA 데이터를 RF 무선 링크를 통해 중앙 처리 노드로 전송하고, 중앙 처리 노드는 기준 부이(reference buoy)에 대한 TDOA를 계산하여 AUV의 위치를 추정한다.
Fig. 1은 이러한 시스템 구조와 신호 흐름을 개념적으로 나타낸 것이다. 회색 점선은 각 부이가 GNSS 위성으로부터 시간·위치 정보를 수신하여 동기화하는 과정을, 노란색 음영 박스는 부이와 중앙 노드가 동일 RF 네트워크에 연결되어 있음을 나타내며, 파란 실선은 AUV ping의 수중 음향 전파 경로를 나타낸다. 부이는 ping의 TOA를 측정하고 이를 RF 링크로 전송하며, 중앙 노드에서는 기준 부이에 대한 TDOA를 계산하여 위치를 산출한다.
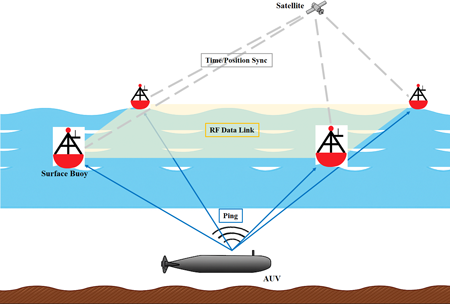
Fig. 1. Conceptual diagram of GNSS-synchronized buoy network for AUV localization.
이러한 구조는 전통적인 LBL 시스템과 달리, 부이 수량과 배치를 임무 환경에 맞추어 유연하게 변경할 수 있으며, 동일 네트워크에서 다수의 AUV를 동시에 추적할 수 있다. 또한 위치 연산과 시간 동기화가 부이 측에서 이루어지므로, AUV의 하드웨어·연산 부담이 크게 줄어든다. 더 나아가 해상 시험장과 같이 외부에서 전 과정의 데이터를 종합·분석한 후, 필요한 핵심 정보만을 AUV로 송신하는 운용 형태에도 적합하여, 운용 편의성과 확장성을 동시에 확보할 수 있다.
본 시스템의 모든 표면 부이는 GNSS 수신기를 통해 자신의 위치 좌표와 PPS 신호를 확보하여, 공통 기준 시각을 유지한다. 이를 통해 각 부이에서 측정한 TOA는 동일한 시간축 상에서 비교 가능하다.
본 연구에서는 AUV가 일정한 수심을 유지하며 수평면에서 이동한다고 가정하였다. 이에 따라 부이 𝑖의 좌표를 ($x_i,y_i$), AUV의 실제 위치를 ($x,y$), 그리고 수중 음속을 $c$라 하면, 부이 $i$와 AUV 사이의 실제 거리는 Eq. (1)과 같이 정의된다.
$$r_i = \sqrt{(x – x_i)^2 + (y – y_i)^2}$$
기준 부이 $j$를 선택했을 때, 부이 $i$와 $j$ 간의 TDOA는 Eq. (2)와 같다.
$$\tau_{ij} = t_i – t_j$$
여기서 $t_i$와 $t_j$는 각각 부이 $i$와 $j$에서 측정한 ping 신호의 도착시각이다. TDOA는 등가 거리 차이로 변환될 수 있으며, Eq. (3)과 같이 표현된다.
$$\Delta r_{ij} = r_i – r_j = c \cdot \tau_{ij}$$
이때, 실제 운용 환경에서는 도착시각 추정 과정의 불확실성은 $\sigma_{t}$로 표현되며, 주요 원인은 PPS 동기화 지터(jitter)와 측정 잡음이다. 이 오차는 위치 추정 정확도에 직접적인 영향을 미치며, TDOA 기반의 하이퍼볼릭 측위식의 오차 전파(error propagation)에 선형적으로 반영된다.
수중에서의 음속은 대략 1410~1570 m/s 범위에서 온도, 염분, 압력 등의 환경 요소에 따라 변동한다. 그러나 본 연구에서는 음속 변화에 따른 영향보다는 부이의 기하학적 배치와 시계 동기 오차가 위치 추정 성능에 미치는 영향에 초점을 두었으므로, 시뮬레이션은 음속을 𝑐 = 1500 m/s로 고정하였다. 이 조건하에서 $\sigma_{t}$를 0.5 ms와 1.0 ms로 설정한 두 가지 경우를 대표 시나리오로 하여 분석을 수행하였다. 이는 상용 GNSS 모듈과 수중 음향 수신기를 조합했을 때 해상 시험 환경에서 현실적으로 달성 가능한 수준이며, 이후 장에서 GDOP 분석 및 동적 추적 성능 평가의 기준값으로 사용된다.
AUV의 위치는 먼저 TDOA 측정값을 기반으로 한 비선형 최소자승법(Nonlinear Least Squares, NLS)으로 산출된다. NLS는 여러 부이에서 수신된 도착시각 차이를 바탕으로 AUV의 위치를 기하학적으로 계산하는 방식으로, 비교적 단순하면서도 정적 환경에서의 성능 평가에 유용하다.
정적 환경에서는 이러한 NLS 결과만으로도 부이 배치, 간격, $\sigma_{t}$의 영향을 명확히 파악할 수 있다. 반면, AUV가 움직이는 동적 환경에서는 단일 추정만으로는 시간에 따른 연속적인 궤적을 안정적으로 얻기 어렵다. 이를 보완하기 위해 본 연구에서는 EKF를 적용하여, NLS 기반의 위치 추정값을 동역학 모델과 결합하고, 측정 잡음을 완화하며 추적 성능을 향상시켰다.
이러한 접근은 정적·동적 조건에서 각각의 강점을 살릴 수 있도록 설계되었으며, NLS와 EKF의 적용 과정과 성능 비교는 이후 장에서 구체적으로 다룬다.
본 절에서는 AUV가 정지한 상태에서 부이 네트워크의 기하 구조와 시각 동기 오차가 위치 추정 성능에 미치는 영향을 분석하였다. 이를 통해 부이 간격 𝐿의 합리적인 범위를 도출하고, 이후 동적 분석에서 사용할 대표 $\sigma_{t}$값을 설정한다. 분석은 2장에서 제시한 측정 모델과 추정 절차를 그대로 적용하였으며, 참조 부이는 최근접 부이(nearest reference) 방식으로 선택하고 Chan & Ho (1994)의 폐형 해를 초기값으로 한 NLS 추정기를 사용하였다.
부이 네트워크는 해수면 위에 정사각형 형상으로 배치된 네 개의 부이로 구성하였다. 부이 간격 𝐿은 600 m에서 1800 m까지 50 m 간격으로 변화시키면서 성능을 비교하였다. 평가 영역은 네 부이로 형성된 면적 내부의 1000 m × 1000 m 정사각형 구역이며, 이를 균일 격자로 분할하여 각 지점에서 몬테카를로 시뮬레이션을 반복 수행하였다.
Fig. 2는 대표적인 네 가지 부이 간격(𝐿 = 600, 1000, 1400, 1800 m)에 대해 해수면에 정사각형으로 배치된 부이 네트워크 형상을 나타낸다. 붉은 삼각형은 부이의 위치를, 노란색 선은 부이 간 기하학적 형상(geometry)을, 청색 음영 영역은 성능 평가를 수행한 1000 m × 1000 m Region of Interest (ROI)를 나타낸다. 이를 통해 부이 간격 변화에 따른 배치 기하 구조와 ROI의 상대적 위치를 직관적으로 비교할 수 있다.
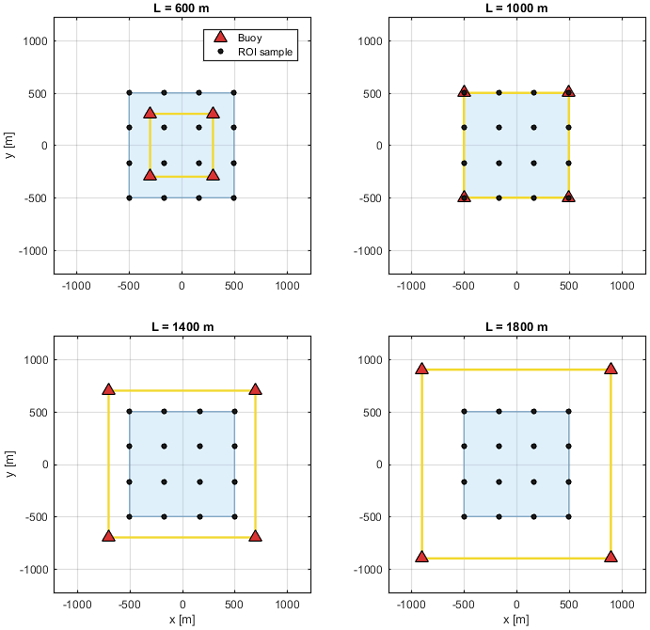
Fig. 2. Square buoy network configurations for selected spacing.
시뮬레이션에서는 $\sigma_{t}$를 채널 전파 손실, 상관 대역폭, PPS 지터 등을 반영하여 모델링하였다. 거리에 따른 신호대잡음비(Signal to Noise Ratio, SNR) 저하와 흡수 손실을 고려하였으며, TOA 추정 오차 분산은 SNR의 역비례 함수로 설정하였다. 본 논문에서는 실무적인 조건을 반영하기 위해 상관 대역폭 𝐵=500 Hz, 동기화 지터 $\sigma_{sync} \approx 0.5 ms$, 확산지수 $n \approx 1.6$, 흡수계수 $\alpha \approx 0.06 \text{dB/km}$를 대표 값으로 사용하였다. 음속은 전술한 바와 같이 𝑐 = 1500 m/s로 고정하였다.
TDOA 기반 위치 추정에서 $\sigma_t$는 GDOP와 곱 형태로 RMSE에 기여한다. 이를 선형 근사하면 Eq. (4)와 같다.
$$\text{RMSE}_{xy} \approx c\, \sigma_{t}\, \text{GDOP}_{TDOA}$$
Eq. (4)에서 $\sigma_t$를 고정하면 RMSE의 𝐿 의존성은 순수하게 기하학적 특성을 반영한다. 반대로 𝐿을 고정하면 RMSE는 $\sigma_t$와 거의 선형적으로 비례한다.
시뮬레이션 결과, 부이 간격 L이 지나치게 작을 경우에는 교차각이 줄어들어 위치 산출 성능이 저하되었고, 반대로 L이 지나치게 크면 거리 증가로 인한 SNR 저하와 TOA 측정 분산 증가가 누적되어 오차가 커졌다. 이 두 요인의 상반된 영향으로 인해 RMSE는 작은 L 영역에서 감소하다가 L≈1 km 전후에서 비교적 안정적인 값으로 유지되었고, 이후에는 완만하게 증가하는 경향을 나타냈다. 이러한 형태는 짧은 간격에서의 기하학적 불리함과 긴 간격에서의 거리 기반 오차 증가가 서로 다른 기울기로 작용한 결과로 해석된다.
Fig. 3은 이러한 경향을 정량적으로 나타낸 것으로, 파란색 실선은 평균 RMSE와 95% 신뢰구간(좌측 축), 빨간색 점선은 90백분위 값(우측 축)을 표시한다. 평균 RMSE는 600 m에서 약 1.6 m 수준에서 시작해 900~1200 m 구간에서 최소 약 1.2 m까지 낮아진 후, 다시 완만히 증가하는 모습을 보인다. 90백분위 값 역시 유사한 패턴을 따르며, 최소값은 약 2.1 m 수준으로 나타났다. 이를 통해, 기하학적 조건과 거리 의존 오차가 균형을 이루는 간격이 존재하며, 이 시뮬레이션에서는 약 1.0–1.2 km 부근이 해당 구간에 해당함을 확인할 수 있다.
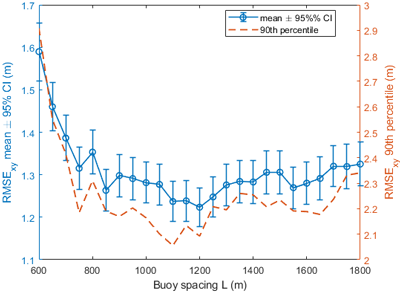
Fig. 3. Mean RMSExy and 90th percentile versus buoy spacing L.
대표 파라미터 조건에서 𝐿=1.2 km일 때 평균 RMSExy는 1.22 m, 상위 10% 분위(p90)는 2.09 m로 나타났으며, 이 구간에서는 간격을 약간 줄이거나 늘려도 성능 저하가 거의 없었다. 이러한 결과는 기하학적 이득과 채널 열화 간의 절충점이 존재함을 보여준다. 이후 동적 분석에서는 𝐿 =1.0 km를 고정값으로 사용한다. 이 값은 평탄 최적대의 중앙에 해당하여 기하·채널·동기화 제약 간 균형을 이루며, 실제 운용 환경에서도 배치 유연성을 확보할 수 있다.
또한 Fig. 4는 L=1.0 km에서 $\sigma_t$를 변화시켰을 때의 RMSExy 변화를 나타낸다. 시뮬레이션 결과는 거의 완벽한 선형 관계($R^2 \approx 0.996$)를 보였으며, $\sigma_t=0.5 \, \text{ms}$와 $1.0 \, \text{ms}$ 지점을 주석으로 표시하여 각각 정밀 동기화와 보급형 동기화 조건을 대표하도록 선정하였다. 이를 통해 이후 장에서 두 조건 간 성능 비교가 가능하도록 기준점을 확립하였다.
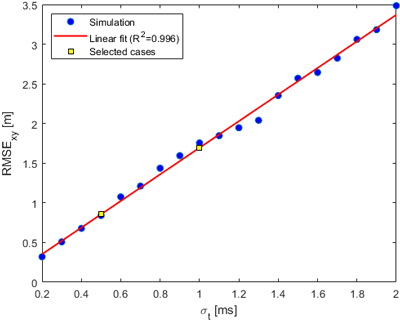
Fig. 4. RMSExy vs. σt at L = 1.0 km.
앞서 3장에서 정적 조건에서의 최적 부이 간격과 시계 동기화 조건을 도출하였다. 그러나 실제 운용 환경에서는 AUV가 이동하면서 위치를 갱신하게 되며, 이때 속도나 갱신 주기와 같은 동적 요인이 위치 정확도에 영향을 미친다. 본 장에서는 이러한 동적 상황에서의 위치 추정 성능을 살펴보고, 필터링 기법을 적용했을 때의 개선 효과를 분석한다.
특히, 부이 네트워크로부터 얻은 개별 위치 추정값을 기반으로 EKF를 적용하여 시계 동기화 오차와 측정 노이즈로 인한 순간적인 위치 변동을 줄이고, 이동 궤적을 보다 안정적으로 추적하는 방법을 다룬다. 분석 대상은 AUV의 이동 속도와 갱신 주기($T_{ping}$)를 변화시키면서, 각 조건에서 필터 적용 전후의 위치 정확도를 비교하는 것이다.
본 연구에서는 AUV의 수평 운동을 등속도(constant velocity) 모델로 근사하였다. 상태 벡터는 위치와 속도 성분으로 구성되며, $k$번째 시각의 상태는 Eq. (5)와 같이 정의된다.
$$\boldsymbol{x}_k
=
\begin{bmatrix}
x_k \quad y_k \quad v_{x,k} \quad v_{y,k}
\end{bmatrix}^{T}$$
여기서 $x_k, y_k$는 위치 좌표, $v_{x,k}, v_{y,k}$는 각각의 속도 성분이다.
상태 전이(state transition)는 ping 주기 $\Delta_t$에 따라 Eqs. (6, 7)과 같이 표현된다.
$$\boldsymbol{x}_{k}
=
\boldsymbol{F}\boldsymbol{x}_{k-1}
+
\boldsymbol{w}_{k-1}$$
$$\mathbf{F}
=
\begin{bmatrix}
1 & 0 & \Delta t & 0 \\
0 & 1 & 0 & \Delta t \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}$$
여기에서 $w_{k-1} \sim \mathcal{N}(0,Q)$는 프로세스 잡음(process noise)이다.
관측 모델은 각 ping 시점에서 NLS로 계산된 2D 위치 추정값 ($\hat{x}_{k},\, \hat{y}_{k}$)을 관측치로 사용한다. 이는 Eqs. (8, 9)와 같이 나타낼 수 있다.
$$\boldsymbol{z}_k
=
\begin{bmatrix}
\hat{x}_k \\
\hat{y}_k
\end{bmatrix}
=
\boldsymbol{H}\,\boldsymbol{x}_k + \boldsymbol{v}_k$$
$$\mathbf{H}
=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{bmatrix}$$
여기서 $v_k \sim \mathcal{N}(0,R)$이며, $R$은 $\sigma_t$와 GDOP를 기반으로 산출한 측정 공분산이다.
본 연구에서 사용한 EKF는 등속도(constant velocity) 상태 모델과 2D 위치 관측모델을 기반으로 하는 표준 구조를 따른다 (Bar-Shalom et al. 2001). 각 ping 주기마다 예측(prediction)과 갱신(update) 단계를 수행하며, 관측치는 NLS로 계산된 2차원 위치 추정 결과를 사용한다. 관측 잡음 공분산은 시계 동기화 오차 $\sigma_t$와 GDOP 값을 통해 산출하며, 관측 결측 시에는 예측 단계만 수행하여 연속적인 추정을 유지한다.
동적 분석에서는 3장에서 도출한 정적 최적 간격 𝐿=1.0 km와 시계 동기화 오차 $\sigma_t$={0.5,1.0} ms를 대표 조건으로 사용하였다. AUV의 수평 속도 $v$는 1 m/s, 3 m/s, 5 m/s, 10 m/s의 네 가지 값을 고려하였으며, ping 주기 $T_{ping}$은 0.5 s, 1.0 s, 2.0 s로 설정하여, 속도와 ping 주기 조합이 성능에 미치는 영향을 평가하였다.
초기 속도는 첫 두 번의 관측 결과로부터 계산하였으며, 관측 불가 구간이 발생하면 해당 스텝은 예측 단계만 수행하였다. 성능 평가는 평균 RMSExy, CEP50, 그리고 EKF 적용 시 NLS 대비 오차 감소율(%)로 수행하였다.
동적 시나리오 시뮬레이션은 3장에서 도출된 정적 기하 최적화 조건(𝐿=1.0 km, 기준 부이=최근접, $\sigma_t$=1.0 ms)에서 수행되었다. AUV의 속도 $v$와 ping 주기 $T_{ping}$을 변화시키며, 속도–주기 조합에 따라 위치 추정 정확도가 어떻게 달라지는지를 분석하였다. 각 조건에서 AUV는 직선 등속 경로를 따라 이동하며, 매 ping 시점에서 NLS로 계산된 2D 위치를 EKF 관측치로 사용하였다. RMSExy는 시뮬레이션 전 구간에 대한 평균값으로 정의하였다.
Fig. 5는 EKF 기반 RMSExy를 ping 간 변위 $d=v \cdot T_{\mathrm{ping}}$ [m]에 대해 나타낸 것이다. 네 가지 속도(𝑣=1, 3, 5, 10 m/s)에서 동일한 경향이 나타나며, 𝑑가 작을수록 RMSE가 완만하게 유지되다가 약 𝑑≈5–6 m 부근부터 급격히 증가한다. 예를 들어, 𝑣=3 m/s에서 $T_{\mathrm{ping}}$ =1.0 s (𝑑=3 m)일 때 RMSE는 약 1.1 m이지만, $T_{\mathrm{ping}}$ =2.0 s (𝑑=6 m)에서는 RMSE가 2 m에 근접한다. 이러한 경향은 속도와 ping 주기 변화에 따른 성능 저하가 ping 간 변위 증가에 직접적으로 기인함을 보여준다.
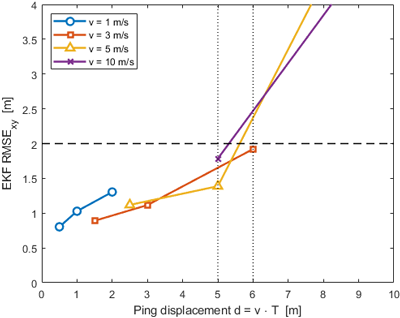
Fig. 5. EKF positioning vs. ping displacement.
Fig. 6은 𝑣=3 m/s, $T_{\mathrm{ping}}$=1.0 s (𝑑=3 m)의 대표 시나리오에서 참 궤적(검은 실선), NLS 추정치(붉은 점), 그리고 EKF 결과(파란 실선)를 비교한 예시이다. NLS 결과에서는 측정 노이즈와 시계 동기화 오차($\sigma_t$=1.0 ms)로 인해 ping 간 위치 변동이 뚜렷하게 나타나지만, EKF 결과는 이러한 고주파 변동을 상당 부분 억제하여 궤적이 참값에 가깝고 부드럽게 재구성된다. 이는 EKF가 순간 오차를 줄이는 것뿐 아니라, 동적 일관성을 강화하여 궤적 품질을 향상시킴을 의미한다.
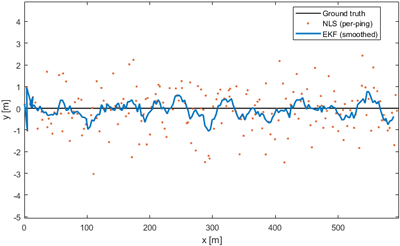
Fig. 6. Example EKF-smoothed trajectory vs. NLS estimates.
이러한 결과를 종합하면 다음과 같다.
1) $v \cdot T_{\mathrm{ping}}$ ≲ 5–6 m 구간에서는 EKF 적용 시 RMSExy를 2 m 이하로 유지할 수 있다.
2) EKF의 상대적 이득은 저속–짧은 주기 조건에서 두드러지며, 이는 ping 간 변위가 작을수록 필터가 시간적 상관성을 효과적으로 활용하기 때문이다.
3 ) 운용 측면에서는 속도와 ping 주기를 적절히 조합해 𝑑를 관리하는 것이 중요하며, EKF는 이러한 제약 내에서 위치 추정 안정성을 크게 향상시킬 수 있다.
본 연구에서는 AUV의 위치 추정 정확도 향상을 위해 부이 네트워크 기반 TDOA 측위 시스템을 대상으로 정적 및 동적 환경에서의 성능을 분석하였다. 정적 기하 분석에서는 부이 간격 𝐿과 $\sigma_t$가 위치 추정 정확도에 미치는 영향을 평가하였다. 시뮬레이션 결과, 간격이 지나치게 작으면 교차각 감소로 기하학적 성능이 저하되고, 반대로 간격이 지나치게 크면 거리 증가로 인한 SNR 저하 및 TOA 측정 분산 증가로 오차가 커졌다. 두 효과가 맞물리면서 𝐿≈1.0–1.2 km 구간에서 평균 RMSExy가 약 1.2 m 수준으로 유지되는 평탄 최적대가 형성됨을 확인하였다. 이를 바탕으로 이후 동적 분석에서는 𝐿=1.0 km를 고정값으로 설정하였다.
동적 분석에서는 EKF를 적용하여 이동 중인 AUV의 위치 추정 성능을 평가하였다. EKF는 시계 동기화 오차와 측정 노이즈로 인한 순간적인 위치 변동을 효과적으로 억제하였으며, 속도–ping 주기($v$–$T_{\mathrm{ping}}$) 조합이 성능에 미치는 영향을 정량적으로 분석하였다. 시뮬레이션 결과, 𝑣⋅$T_{\mathrm{ping}}$ ≲5–6 m 범위에서 RMSExy가 2 m 이하로 유지되었으며, EKF 적용 시 NLS 대비 20–50%의 개선 효과를 확인하였다. 특히, 속도가 낮고 ping rate가 높은 조건에서 성능 향상이 가장 크게 나타났다.
정적–동적 통합 분석을 통해, 부이 간격·시계 동기화 정밀도·이동 속도·ping 주기 등 주요 설계 및 운용 변수가 위치 정확도에 미치는 상관관계를 종합적으로 파악하였다. 이를 통해 실제 운용 환경에서 안정적인 성능을 유지할 수 있는 조건 범위를 확인하였으며, 이러한 결과는 시스템 배치와 운용 스케줄을 설계하는 데 참고가 될 수 있다. 또한, EKF 적용을 통해 다양한 시나리오에서 순간적인 위치 변동이 효과적으로 억제되고, 전반적인 위치 추정 정확도가 향상됨을 확인하였다.
향후에는 본 연구에서 제시한 분석 방법을 보다 다양한 해양 환경 조건에 확장하고, 해류·다중경로·음속 분포 변화와 같은 현실적인 해양 요소를 반영한 시뮬레이션을 수행할 예정이다. 이를 통해 다양한 운용 시나리오에서의 신뢰도를 높이고, 시스템 설계 및 최적화에 적용 가능한 범용성을 확보하고자 한다.
Conceptualization, C.H.; methodology, C.H. and H.K.; software, C.H. and H.K.; validation, C.H., D.K., and S.L.; formal analysis, C.H. and H.K.; investigation, C.H. and D.K.; resources, D.K. and S.L.; data curation, C.H.; writing—original draft preparation, C.H.; writing—review and editing, C.H., H.K., and D.K.; visualization, C.H. and H.K.; supervision, C.H.
The authors declare no conflict of interest.
Aparicio, J., Jiménez, A., Álvarez, F. J., Ruiz, D., De Marziani, C. et al. 2016, Characterization of an underwater positioning system based on GPS surface nodes and encoded acoustic signals, IEEE Transactions on Instrumentation and Measurement, 65, 1773-1784. https://doi.org/10.1109/TIM.2016.2552699
Bar-Shalom, Y., Li, X. R., & Kirubarajan, T. 2001, Estimation with applications to tracking and navigation: theory, algorithms and software (New York, NY: John Wiley & Sons, Inc.).
Chan, Y. T. & Ho, K. C. 1994, A simple and efficient estimator for hyperbolic location, IEEE Transactions on Signal Processing, 42, 1905-1915. https://doi.org/10.1109/78.301830
Han, Y., Zheng, C., & Sun, D. 2015, Accurate underwater localization using LBL positioning system, In OCEANS 2015 – MTS/IEEE Washington, Washington, DC, USA, 19-22 October 2015, pp.1-4. https://doi.org/10.23919/OCEANS.2015.7401893
Kilfoyle, D. B. & Baggeroer, A. B. 2000, The state of the art in underwater acoustic telemetry, IEEE Journal of Oceanic Engineering, 25, 4-27. https://doi.org/10.1109/48.820733
Otero, P., Hernández-Romero, Á., Luque-Nieto, M. Á., & Ariza, A. 2023, Underwater positioning system based on drifting buoys and acoustic modems, Journal of Marine Science and Engineering, 11, 682. https://doi.org/10.3390/jmse11040682
Paull, L., Saeedi, S., Seto, M., & Li, H. 2014, AUV navigation and localization: A review, IEEE Journal of Oceanic Engineering, 39, 131-149. https://doi.org/10.1109/JOE.2013.2278891
Shaukat, N., Ali, A., Iqbal, M. J., Moinuddin, M., & Otero, P. 2021, Multi-sensor fusion for underwater vehicle localization by augmentation of RBF neural network and error-state Kalman filter, Sensors, 21, 1149. https://doi.org/10.3390/s21041149
Stojanovic, M. & Preisig, J. 2009, Underwater acoustic communication channels: Propagation models and statistical characterization, IEEE Communications Magazine, 47, 84-89. https://doi.org/10.1109/MCOM.2009.4752682
Zhang, T., Chen, L., & Li, Y. 2016, AUV underwater positioning algorithm based on interactive assistance of SINS and LBL, Sensors, 16, 42. https://doi.org/10.3390/s16010042