1Department of Electrical and Computer Engineering, Inha University, Incheon 22212, Korea
2Department of Geoinformatic Engineering, Inha University, Incheon 22212, Korea
3PP-Solution Inc., Seoul 08504, Korea
Citation: Noh, N.-W. & Park, K.-D. 2025, Comparison of Static and Kinematic GNSS Positioning Performance Using Qinertia Software, Journal of Positioning, Navigation, and Timing, 14, 321-330.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2025 September, Volume 14, Issue 3, pages 321-330. https://doi.org/10.11003/JPNT.2025.14.3.321
Received on Aug 12, 2025, Revised on Aug 23, 2025, Accepted on Aug 28, 2025, Published on Sep 15, 2025.
Copyright © The Institute of Positioning, Navigation, and Timing
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This study evaluates the performance of Global Navigation Satellite System (GNSS) data processing using the Qinertia software (SBG Systems). Three processing modes—Single Base Station (SBS) Post-Processing Kinematic (PPK), Virtual Base Station (VBS) PPK, and Precise Point Positioning (PPP)—were applied to both static and kinematic positioning scenarios. The results were compared against coordinates derived from the high-precision GipsyX scientific software as well as real-time highaccuracy methods including Real-Time Kinematic (RTK) and Virtual Reference Station (VRS) RTK. For static positioning, all three methods achieved high accuracy, with average horizontal and vertical root mean square error (RMSE) of 0.8 cm and 1.5 cm, respectively, relative to GipsyX and RTK reference solutions. Notably, VBS PPK maintained a fix rate of approximately 99% for baseline distances exceeding 30 km. In kinematic positioning, both SBS-PPK and VBS-PPK achieved centimeter-level accuracy compared to VRS-RTK. Under open-sky conditions, average horizontal and vertical RMSE were 3.5 cm and 2.5 cm, respectively, while in dense urban environments they were 3.0 cm and 5.8 cm. Performance differences between the two PPK methods under open-sky conditions were minimal, within about 1-2 cm.
GNSS, Qinertia, PPK, PPP, RTK
Global Navigation Satellite System (GNSS) is widely used due to its capability of estimating a user’s position with only four satellites (Hofmann-Wellenhof et al. 2001). GNSS is applied not only to various modes of transportation, such as ships, aircraft, and automobiles, but also to personal devices, including smartphones. Accordingly, many research institutes are actively developing GNSS-based positioning algorithms and validating their performance through comparative analyses with precise reference coordinates. These reference coordinates are obtained using high-precision positioning methods such as GipsyX, Real-Time Kinematic (RTK), and Virtual Reference Station (VRS) RTK.
GipsyX, developed by the Jet Propulsion Laboratory (JPL), is a high-precision GNSS data processing software that generates precise coordinates based on Precise Point Positioning (PPP) and is widely used for coordinate and velocity estimation (Ha et al. 2021). It computes precise positions by applying GNSS orbit and clock products from the International GNSS Service (IGS) or JPL—available in precise, rapid, and ultra-rapid forms—together with various error correction models. The accuracy depends on the product type, with the precise product providing the highest accuracy but requiring more than two weeks for availability. Meanwhile, the ultra-rapid product achieves accuracies of about 3-5 cm and is available within approximately two hours (Ha et al. 2012). Therefore, GipsyX has inherent limitations in providing precise coordinates in real time.
RTK is a positioning technique that computes centimeter-level coordinates in real time by receiving correction data from a single reference station, typically via NTRIP or TCP/IP protocols. This approach is advantageous due to its simplicity and rapid connectivity. However, as the baseline distance from the reference station increases to several tens of kilometers, the spatial correlation of atmospheric errors (ionospheric and tropospheric) diminishes, resulting in longer times for integer ambiguity resolution (AR) and a reduced likelihood of obtaining fixed solutions. Furthermore, RTK is less applicable in areas with sparse or no reference station infrastructure (El-Mowafy 2012).
In contrast, VRS-RTK is a type of network RTK that utilizes data from multiple base stations to generate a virtual reference station near the user, thereby providing correction information. This method offers the advantage of maintaining high accuracy over wide areas without baseline distance limitations. However, it is highly dependent on communication networks such as LTE or Wi-Fi, and when the communication environment is unstable, correction information may not be received reliably, leading to failure to obtain a fixed solution or to meter-level positioning errors (No et al. 2012).
As an alternative to these limitations, Qinertia, developed by SBG Systems, has been attracting increasing attention. Qinertia is a tightly coupled post-processing software that integrates GNSS and Inertial Navigation System (INS) data (SBG SYSTEMS 2025). It is applicable to diverse mobile platforms, including vehicles, drones, ships, and aircraft. For GNSS applications, it offers centimeter-level positioning accuracy through three data processing modes: Single Base Station (SBS) Post-Processing Kinematic (PPK), Virtual Base Station (VBS) PPK, and Precise Point Positioning (PPP). Among these, the PPK method uses the Receiver INdependent Exchange (RINEX) data from reference stations, enabling precise position estimation without constraints in communication conditions or baseline length, and previous studies have reported that it can achieve accuracy within 1-10 cm compared with RTK (Saidani et al. 2020). However, there has been insufficient quantitative evaluation of Qinertia’s data processing performance in Korea. In particular, empirical assessments are lacking on whether SBS-PPK and VBS-PPK results can serve as reference coordinates, providing a viable alternative to GipsyX or RTK.
This study evaluates the accuracy and applicability of three GNSS data processing modes in Qinertia—SBS-PPK, VBS-PPK, and PPP—applied to both static and kinematic positioning cases. Section 2 provides an overview of Qinertia along with a summary of the principles and technical distinctions of each data processing method. Section 3 presents a quantitative accuracy assessment based on processing results obtained with Qinertia using RINEX data supplied by the domestic GNSS reference station service operated by PPSOL Co., Ltd. (PPSOL, https://ppsol.com). For static positioning, results processed using GNSS RINEX data collected at a fixed receiver were compared with reference coordinates from GipsyX and RTK. For kinematic positioning, results processed from RINEX data collected during vehicle operation were compared to reference coordinates from VRS-RTK. The performance of the three methods was evaluated using metrics such as root mean square error (RMSE), standard deviation (SD), and bias to assess the practical applicability and reliability of Qinertia’s processing capabilities.
This section provides an overview of the Qinertia software, its data processing methods, and the data used for performance validation. In this study, only GNSS data were processed with Qinertia, which supports multiple GNSS processing modes, including SBS-PPK, VBS-PPK, and PPP. Qinertia also improves overall positioning accuracy by automatically selecting reliable data through quality control techniques such as Receiver Autonomous Integrity Monitoring (RAIM) applied to the received GNSS signals. For rover data processing, users may either manually input reference station data or allow the software to automatically download data from nearby Continuously Operating Reference Stations (CORS).
Qinertia provides three types of data processing results: Forward, Backward, and Merged. The Forward solution processes GNSS data in the forward time direction, while the Backward solution processes it in the reverse direction. The Merged solution combines both results to minimize errors and achieve the highest accuracy. It is generally regarded as the most reliable reference among the data processing outputs. In addition, a fixed solution in Qinertia indicates that the integer ambiguity of the GNSS carrier phase has been successfully resolved through the AR technique, which serves as a key indicator of high-accuracy results. Conversely, failure of AR yields a float solution, which has relatively lower accuracy.
In this analysis, a total of seven permanent stations were used, including IHUA and IHUB located on the rooftop of Building 4 at Inha University, and PPHQ, PPHS, PPGH, PPCH, and PPYJ operated by PPSOL. The receiver and antenna specifications for each site, along with their coordinates as of September 1, 2023, are summarized in Table 1. The reference frame for these coordinates is IGb14 as defined by the IGS, and the coordinates of the antenna reference point (ARP) were calculated using GipsyX. Fig. 1 presents the geographical location of IHUB, where the baseline distance between IHUB and IHUA is very short at 0.983 m. Fig. 2 presents the locations of PPHS (Hwaseong), PPGH (Ganghwa), PPCH (Pocheon), and PPYJ (Yeoju). Finally, Fig. 3 presents the location of PPHQ (Seoul).
Table 1. Base stations used in Qinertia processing. All the antennas are fitted with SCIS radomes.
| Site | Receiver | Antenna | ECEF [m]: IGb 14 Coordinates @ Sep 1st, 2023 | ||
|---|---|---|---|---|---|
| X | Y | Z | |||
| IHUA | Septentrio AsteRx SB3 | TWIVC6150 | -3026676.332 | 4067187.742 | 3857246.827 |
| IHUB | Septentrio AsteRx SB3 | TWIVC6150 | -3026675.527 | 4067188.306 | 3857246.748 |
| PPHQ | Javad TRE_3L | TWIVC6050 | -3041232.493 | 4053906.693 | 3859927.421 |
| PPHS | Septentrio AsteRx SB | JAVRINGANT_DM | -3049045.924 | 4071455.693 | 3835250.836 |
| PPGH | Javad TRE_3SDELTA | JAVRINGANT_DM | -3003051.620 | 4059905.969 | 3838100.055 |
| PPCH | Septentrio AsteRx SB Pro | JAVRINGANT_DM | -3047202.244 | 4014485.287 | 3895961.513 |
| PPYJ | Javad TRE_3S | JAVRINGANT_DM | -3102739.141 | 4023043.419 | 3843228.700 |
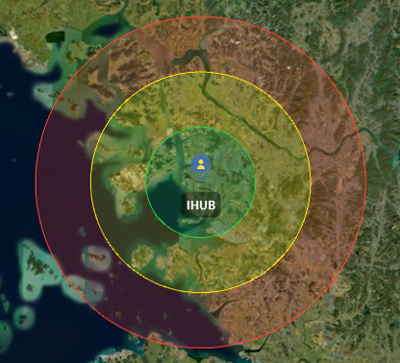
Fig. 1. SBS-PPK coverage map for the base station of IHUB.
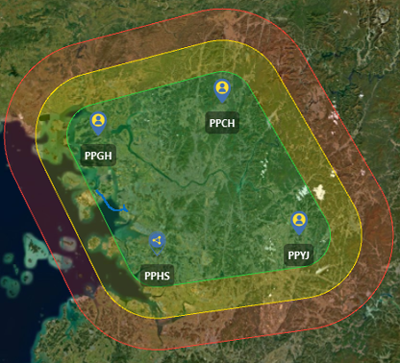
Fig. 2. VBS-PPK coverage map for four base stations of PPHS, PPGH, PPCH, and PPYJ.
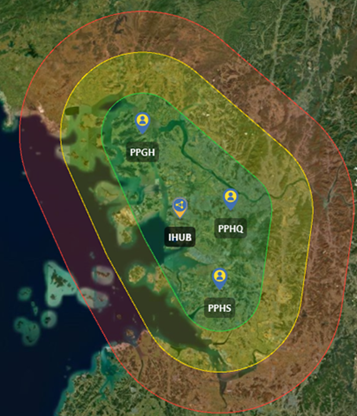
Fig. 3. VBS-PPK coverage map for four base stations of PPHS, IHUB, PPGH, and PPHQ.
SBS-PPK is a positioning method that post-processes RINEX data from a rover station using RINEX data from a specific base station. It assumes a short baseline distance between the base and rover, typically less than 20 km, and provides fixed solutions by performing AR with the double-difference technique to mitigate common errors such as satellite orbit, clock, and atmospheric effects. However, as the baseline distance increases, the similarity of atmospheric conditions between stations decreases, which reduces AR feasibility and increases positioning errors. Consequently, accuracy degrades and the likelihood of failing to obtain fixed solutions grows. Performance degradation generally begins when the baseline exceeds 20 km, and AR becomes fundamentally difficult beyond 60 km.
Fig. 1 illustrates the implementation of SBS-PPK with IHUB designated as the base station, highlighting the performance limitations based on baseline distance. The green circle, with a radius of approximately 20 km, indicates an area where stable fixed solutions are expected. The yellow circle, with a radius of about 40 km, marks a boundary zone where AR performance may become challenging and accuracy may deteriorate. The red circle, with a radius of approximately 60 km, represents a range where achieving AR is difficult.
VBS-PPK is a positioning method that uses RINEX data from multiple base stations to generate a virtual base station near the rover in post-processing. The core of this method is to precisely model the error characteristics around the rover, which requires at least three base stations to operate. Among these, one must be designated as the Master Base, serving as the reference point within the network. The Master Base calculates the ionospheric residuals between itself and the other base stations using long-baseline RTK. It then applies spatial interpolation with Least Squares Collocation (LSC) to estimate the ionospheric errors near the rover. By default, the Master Base is automatically selected based on Qinertia’s quality control methods, but it can also be specified manually by the user. The virtual base station generated through these principles is configured to maintain a short baseline to the rover, which allows double-difference and AR to be performed more stably and enables precise positioning.
Due to its ability to accurately model ionospheric errors, VBS-PPK provides stable and highly accurate positioning results over wide areas without baseline constraints. As a result, it can maintain robust performance even in environments with widely spaced reference stations or where RTK is impractical. However, when the quality of the reference station data forming the network is low or observations at certain epochs are missing, the accuracy of error correction may degrade and fixed solutions may not be achieved.
Figs. 2 and 3 are examples of VBS-PPK implementation based on networks composed of four base stations in each case, with PPHS, PPGH, PPCH, and PPYJ in Fig. 2 and PPHS, IHUB, PPGH, and PPHQ in Fig. 3. The green area indicates the network center, where a rover station can be expected to achieve a stable fixed solution. The yellow area represents a boundary zone at a greater distance from the network, where AR performance may become difficult or accuracy may degrade. The red area represents the outer boundary of the network, where imbalances in baseline geometry make successful AR unlikely. These observations demonstrate that although VBS-PPK performance is influenced by the spatial configuration of the reference station network, it has the advantage of achieving centimeter-level positioning accuracy over wide areas.
PPP is a positioning method that estimates the receiver position independently by utilizing precise orbit and clock correction information without relying on base station data (Lee & Park 2020). Precise positions are obtained by correcting for various error sources, including satellite orbit and clock errors, phase center offsets and variations of satellite and receiver antennas, and ionospheric and tropospheric delays. Qinertia performs PPP processing using precise correction products from the International GNSS Service (IGS) and other providers.
In this section, the data processing performance of Qinertia is quantitatively evaluated in both static (S) and kinematic (K) positioning environments. The static analysis consists of four cases. In S1, SBS-PPK is evaluated using 24-hour datasets from GPS, Global Navigation Satellite System (GLONASS), Galileo, and BeiDou constellations. In S2, under the same receiving conditions, 1-hour datasets are evaluated with two constellation configurations—GPS, Galileo (G+E) and GPS, GLONASS, Galileo, and BeiDou (G+R+E+C)—to assess the effect of constellation expansion. In S3, the accuracy of VBS-PPK is evaluated when the network is configured with either three or four base stations. In S4, the performance of PPP in terms of fixed and float solutions is evaluated using 24-hour datasets from GPS, Galileo, and BeiDou (G+E+C). All static cases are evaluated against reference coordinates derived from GipsyX and RTK, with detailed configurations summarized in Table 2.
Table 2. Details on test setups for four static (S) cases and two kinematic (K) cases.
| Case | Processing | Constellation | Data span (hours:mins) | Reference |
|---|---|---|---|---|
| S1 | SBS-PPK | G+R+E+C | 24:00 | GipsyX |
| S2 | G+E, G+R+E+C | 01:00 | RTK | |
| S3 | VBS-PPK | G+R+E+C | 24:00 | GipsyX |
| S4 | G+E+C | |||
| K1 | PPK | G+R+E+C | 00:15 | VRS-RTK |
| K2 | 00:45 |
The final two cases in Table 2 correspond to kinematic analyses, in which the performance of SBS-PPK and VBS-PPK is evaluated using rover datasets of 15 minutes and 45 minutes for K1 and K2, respectively. Both cases use G+R+E+C constellations, and accuracy is evaluated against reference coordinates derived from VRS-RTK. Detailed descriptions of each test case, together with the positioning results, are provided in sub-sections 3.1 and 3.2.
For each case, GipsyX and RTK are taken as reference solutions, and dX, dY, dZ errors in the three-dimensional Cartesian coordinate system are computed by comparing them with the coordinates obtained from Qinertia. These errors are then converted into dN, dE, dV errors in the north-south, east-west, and vertical directions of the topocentric coordinate system, which are subsequently used to calculate RMSE, SD, and bias.
Case S1 evaluates the results of processing 24 hours of RINEX data using the SBS-PPK method with the GipsyX reference coordinates in two configurations, one with IHUA as the rover station and IHUB as the base station, and the other with IHUB as the rover station and IHUA as the base station. As shown in Table 1, both IHUA and IHUB are permanent stations equipped with high-grade geodetic surveying instruments, including Septentrio AsteRx SB3 receivers and Tallysman choke-ring antennas. The ARP distance between the two stations is only 0.983 m. Thus, this experiment evaluates the accuracy of data processing with a baseline shorter than 1m and assesses Qinertia’s ability to deliver precise results over such short baselines.
The 24-hour dataset collected on June 12, 2025, at 30-second intervals is processed, and the differences between the SBS-PPK results and the GipsyX reference coordinates are less than 0.3 cm in terms of RMSE in the three directions, with the horizontal RMSE as small as 0.1 cm. These results indicate that SBS-PPK provides highly reliable performance for static positioning over short baselines. While PPK generally produces coordinates at each sampling epoch, Qinertia also provides a batch-processing mode that generates a single coordinate estimate for the entire duration of the RINEX file. According to the batch-processing results, the rover station coordinates, regardless of the base station, differ by 0.06 cm in the north-south direction, 0.01-0.02 cm in the east-west direction, and 0.27-0.34 cm in the vertical direction, corresponding to horizontal differences of less than 1 mm and approximately 3 mm vertically. Overall, these findings confirm that the SBS-PPK approach is capable of achieving millimeter-level positioning accuracy when applied to geodetic-grade receivers over very short baselines.
In Case S2, a tripod and tribrach were temporarily installed on the rooftop of Building 4 at Inha University, and a Javad G5T antenna was connected to an RTAP2U receiver (Kim et al. 2021) to collect RINEX data at 1-second intervals. This dataset represents observations obtained with a lower-cost receiver compared to the S1 case. The experiment was conducted for one hour, from UT 07:43:00 to 08:42:59 on May 19, 2025. As shown in Fig. 4, this temporary dataset was designated CAMP, and the baseline to each of the two reference stations was shorter than 3.4 m.
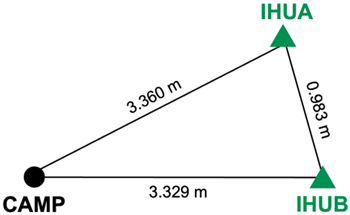
Fig. 4. Geometry and baseline distances of the campaign site CAMP with respect to the base stations of IHUA and IHUB.
The latest version of Qinertia is capable of processing data from all four global navigation satellite constellations, G+R+E+C. However, at some GNSS stations, the receivers are capable of receiving all four types of satellite navigation signals, but only G+E data are available. Thus, the objective of the S2 experiment is to compare positioning performance with respect to constellation expansion. The collected 1-hour dataset is processed using both the G+E and G+R+E+C configurations, and the results are compared with RTK reference coordinates from IHUA. The horizontal errors are presented in Fig. 5, and the RMSE, SD, and bias in the three coordinate directions are summarized in Table 3.
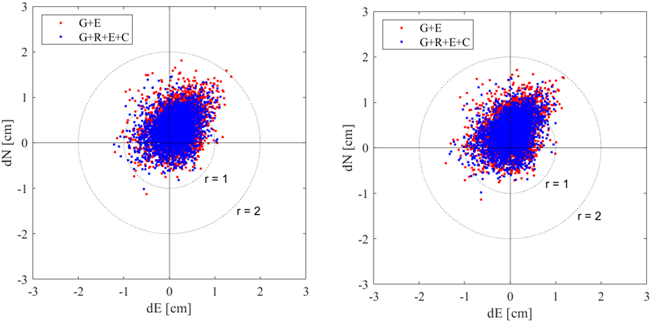
Fig. 5. Horizontal errors for the S2 case: (left) positioning errors of CAMP with IHUA as a single base; (right) positioning errors of CAMP with IHUB as a single base.
Table 3. RMSE, SD and bias for each dN, dE, dV direction for the S2 case.
| Metric [cm] | Direction | IHUA as single base | IHUB as single base | ||||
|---|---|---|---|---|---|---|---|
| G+E | G+R+E+C | G+E | G+R+E+C | ||||
| RMSE | dN | 0.55 | → | 0.45 | 0.55 | → | 0.48 |
| dE | 0.37 | → | 0.34 | 0.33 | → | 0.32 | |
| dV | 0.97 | → | 0.83 | 0.92 | → | 0.77 | |
| SD | dN | 0.38 | → | 0.32 | 0.39 | → | 0.34 |
| dE | 0.33 | → | 0.32 | 0.33 | → | 0.32 | |
| dV | 0.75 | → | 0.73 | 0.74 | → | 0.71 | |
| bias | dN | 0.39 | → | 0.31 | 0.38 | → | 0.34 |
| dE | 0.16 | → | 0.12 | 0.03 | → | 0.02 | |
| dV | 0.61 | → | 0.39 | 0.55 | → | 0.30 | |
As shown in Fig. 5, in the G+E constellation, most horizontal errors fall within a circle of approximately 2 cm in radius, whereas in the G+R+E+C constellation, they are more tightly concentrated within about 1 cm. The horizontal RMSE is 0.65 cm for G+E and 0.57 cm for G+R+E+C. As shown in Table 3, the three metrics—RMSE, SD, and bias—consistently show better performance for G+R+E+C, regardless of the base station or coordinate direction. Notably, consistent results were obtained for both IHUA and IHUB, confirming that the G+R+E+C based SBS-PPK method can provide stable sub-centimeter accuracy under favorable observation conditions.
The S3 case evaluates 24-hour RINEX data using the VBS-PPK method, which applies a network-based approach. The analysis focuses on the permanent station PPHQ, located on the rooftop of the PPSOL headquarters, with its equipment specifications summarized in Table 1. The 24-hour dataset collected on June 14, 2025, at 30-second intervals is processed using Qinertia’s VBS-PPK mode, and the results are compared with reference coordinates from GipsyX. To assess the effect of the number of base stations on coordinate differences, the network is configured with either four or three stations. The four-station configuration corresponds to the layout shown in Fig. 2, while in the three-station configuration, PPYJ, the easternmost site with the longest baseline from PPHQ, is excluded. The baseline lengths from PPHQ are 31 km to PPHS, 45 km to PPGH, 54 km to PPCH, and 71 km to PPYJ.
The positioning errors from the S3 case are presented for each direction in Fig. 6, while Fig. 7 shows the RMSE values for different numbers of base stations as a bar chart. As shown in Fig. 6, the results indicate that, regardless of the number of base stations, the average horizontal RMSE remains within 2 cm and the vertical RMSE within 3 cm. In addition, the RMSE, SD, and bias for all directions are within 3 cm. However, increasing the number of base stations from three to four results in a slight increase in the vertical error. This is likely due to the inclusion of PPYJ, located about 71 km from the rover station, suggesting that incorporating a base station with an excessively long-baseline in VBS-PPK processing can degrade accuracy in specific direction. Therefore, in VBS-PPK data processing, careful selection of base stations within an appropriate baseline range is essential to ensure reliable positioning accuracy.
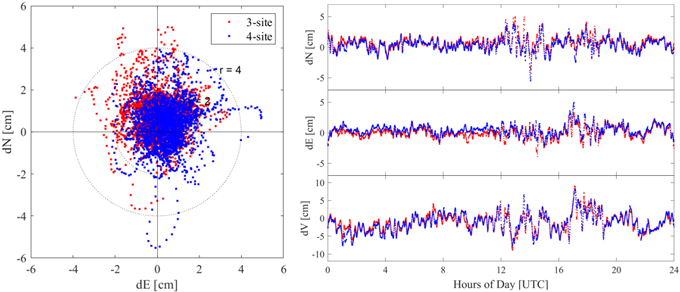
Fig. 6. Scatters of horizontal errors (left) and time series of dN, dE, and dV for the case of S3 (right).
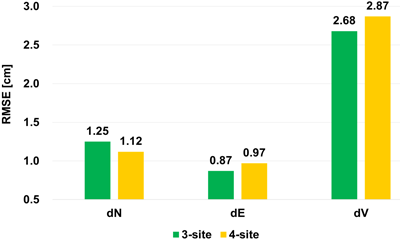
Fig. 7. RMSE comparison in each direction between 3-site vs 4-site VBSPPP processing.
In the S4 case, 24-hour RINEX data are processed in PPP mode to generate daily fixed and float solutions to evaluate which option provides higher accuracy. The analysis focuses on the permanent station PPHQ, located on the rooftop of PPSOL headquarters, with its equipment specifications summarized in Table 1. The 24-hour datasets collected between June 11 (DOY 162) and June 17 (DOY 168), 2025, at 30-second intervals are batch-processed using Qinertia’s PPP mode, and the results are compared with coordinates from GipsyX. Fig. 8 presents the coordinate errors for each direction over the 7-day period. Based on the experimental results, the horizontal RMSE is 0.41 cm for the fixed solution and 0.84 cm for the float solution. In the east-west direction, however, the bias is 0.15 cm for the fixed solution, whereas the float solution shows a relatively large bias of -0.72 cm. This difference is also evident in the east-west time series of Fig. 8. Overall, the PPP fixed solution confirms that stable precision within 1 cm can be achieved in all three directions.
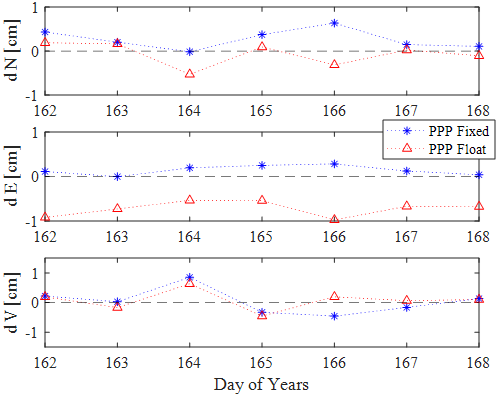
Fig. 8. Time series of dN, dE, and dV for the case of S4.
For each case, the VRS-RTK coordinates are set as the reference, and the dX, dY, dZ errors are calculated by comparing them with the coordinates derived from Qinertia. These errors are then converted into dN, dE, dV errors, from which RMSE, SD, and bias are calculated. The analysis also compares the accuracy of the SBS-PPK method, which uses a base station located within about 10 km of the rover, with that of the VBS-PPK method employing four base stations. In both cases, either a single base station (IHUB) or a network consisting of IHUB, PPHQ, PPHS, and PPGH is used, with the station locations and network configuration shown in Fig. 3.
In the K1 case, RINEX data was collected at 1-second intervals during a 5 km vehicle drive for approximately 15 minutes, from 07:18 to 07:34 on April 25, 2025, in both open and semi-urban areas near Solchan Park in Songdo, Incheon. The trajectory is shown on Fig. 9. The data, acquired with an RTAP2U receiver and a Javad G5T antenna, are processed using both SBS-PPK and VBS-PPK methods, and the results are compared with VRS-RTK reference coordinates. The average baseline distances between the rover and each base station are 8.2 km for IHUB, 25 km for PPHQ, 26 km for PPHS, and 43 km for PPGH.
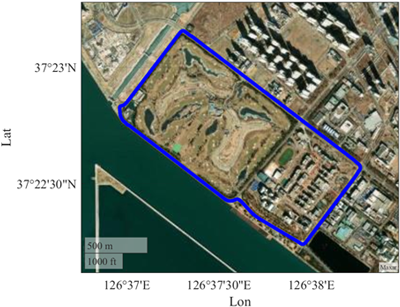
Fig. 9. Vehicle trajectory in the K1 case. The total length is about 5 km.
As shown in Fig. 10 and Table 4, both methods achieve horizontal and vertical RMSE within 4 cm and 3 cm, respectively, with RMSE, SD, and bias for all directions remaining within 5 cm. Notably, SBS-PPK yields slightly lower errors than VBS-PPK, indicating that when observation conditions are favorable and a nearby base station is available, high accuracy can be achieved with SBS-PPK alone. Both methods achieved a fixed solution rate of approximately 99%.
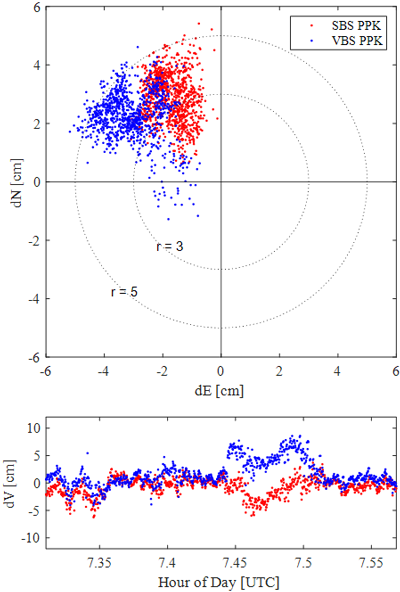
Fig. 10. Scatters of horizontal errors (up) and time series of dV for the case of K1 (down).
Table 4. RMSE, SD, and bias for each dN, dE, dV direction in the K1 case.
| Metric [cm] | Direction | Processing method | |
|---|---|---|---|
| SBS-PPK | VBS-PPK | ||
| RMSE | dN | 2.99 | 2.67 |
| dE | 1.81 | 3.21 | |
| dV | 1.78 | 2.97 | |
| SD | dN | 0.82 | 1.40 |
| dE | 0.57 | 0.94 | |
| dV | 1.63 | 2.49 | |
| bias | dN | 2.87 | 2.28 |
| dE | -1.71 | -3.07 | |
| dV | -0.72 | 1.63 | |
However, during the 7.45-7.50 h interval in Fig. 10, when the trajectory transitions from an open-sky area to a semi-urban environment, both methods exhibit increased vertical errors due to AR failures for some satellites, reducing the number of fixed solutions. The increase is more pronounced in VBS-PPK, likely because changes in the observation environment weaken the spatial correlation of ionospheric errors and degrade correction accuracy. These findings confirm that variations in observation conditions directly affect the positioning accuracy of VBS-PPK.
In the K2 case, RINEX data was collected at 1-second intervals during a 25 km drive lasting approximately 45 minutes, from 07:47 to 08:35 on June 12, 2025, along the route between Incheon International Airport and Inha University. The trajectory is shown on Fig. 11. The route includes open-sky areas, urban areas, and GNSS signal-blocked sections. RINEX data acquired with an RTAP2U receiver and a Javad G5T antenna are processed using both SBS-PPK and VBS-PPK methods, and the results are compared with VRS-RTK reference coordinates. The average baseline distances between the rover and each base station are 9.7 km for IHUB, 29 km for PPHQ, 34 km for PPGH, and 36 km for PPHS.

Fig. 11. Vehicle trajectory in the K2 case. The total length is about 25 km.
The K2 results, analyzed using the same procedure as in the K1 case, are presented in Fig. 12 and Table 5. In Fig. 12, the gap in the graph between 7.9 and 8.0 h corresponds to a period when the VRS-RTK solution remains in a float state while the vehicle passes near an overpass and the Incheon Bridge tollgate. This interval is excluded from the analysis. Abrupt variations in the positioning results at other times correspond to segments where the vehicle enters or exits dense urban areas or passes beneath elevated roadways.
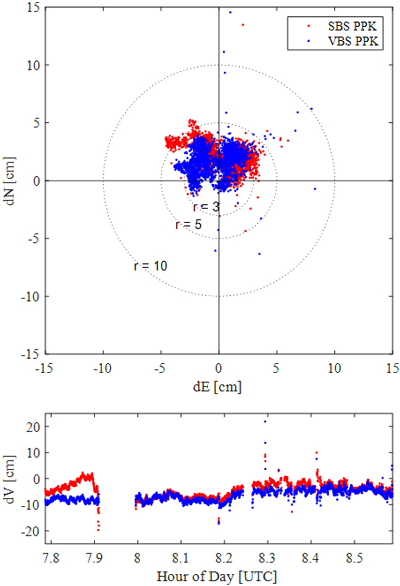
Fig. 12. Scatters of horizontal errors (up) and time series of dV for the case of K2 (down).
Table 5. RMSE, SD, and bias for each dN, dE, dV direction in the K2 case.
| Metric [cm] | Direction | Processing method | |
|---|---|---|---|
| SBS-PPK | VBS-PPK | ||
| RMSE | dN | 2.43 | 2.04 |
| dE | 1.93 | 1.68 | |
| dV | 5.20 | 6.84 | |
| SD | dN | 1.06 | 1.17 |
| dE | 1.90 | 1.65 | |
| dV | 2.77 | 2.23 | |
| bias | dN | 2.18 | 1.66 |
| dE | 0.33 | -0.31 | |
| dV | -4.40 | -6.47 | |
As shown in Table 5, both processing methods achieve horizontal RMSE within 3 cm and vertical RMSE within 7 cm, with RMSE, SD, and bias for all directions remaining below 7 cm. Both methods also attain a fixed solution rate of approximately 90%. However, Fig. 12 shows that while the horizontal errors of SBS-PPK are distributed within a 5 cm radius, those of VBS-PPK are more tightly concentrated within 3 cm, indicating that VBS-PPK provides higher accuracy. Taken together, these results suggest that under constrained observation conditions in kinematic environments, VBS-PPK delivers greater accuracy than SBS-PPK, in contrast to the K1 case.
In this study, the performance of three Qinertia processing methods was evaluated through a series of static and kinematic positioning cases, with accuracy assessed against reference coordinates from GipsyX, RTK, and VRS-RTK. In static cases, all methods achieved errors at most 3 cm. In Case S1 (SBS-PPK batch-processing), the results showed sub-millimeter-level accuracy in horizontal direction and approximately 3 mm in vertical. In Case S2 (SBS-PPK with the G+R+E+C constellation), the horizontal RMSE was 0.57 cm, demonstrating high accuracy. Case S3 (VBS-PPK) yielded horizontal and vertical RMSE values within 2 cm and 3 cm, respectively, while Case S4 (PPP) achieved a horizontal RMSE of 0.41 cm in the fixed daily solution, demonstrating stable precision. These findings confirm that in static positioning, all evaluated methods can attain high accuracy and precision. Notably, high performance was maintained even with reference stations located 30-70 km from the rover, demonstrating the robustness of these methods over long baselines. In kinematic cases, both SBS-PPK and VBS-PPK achieved errors within 7 cm. In Case K1, where the baseline was short and observation conditions were favorable, SBS-PPK alone achieved sufficient accuracy. In contrast, in Case K2, which involved challenging environments such as dense urban areas, VBS-PPK produced more stable results. These findings highlight the importance of selecting the appropriate processing method according to the observation environment. Although this study was conducted using GNSS only data, the results demonstrated the high accuracy of Qinertia’s processing across various cases. In future work, the integration of GNSS and INS data is expected to further enhance the performance validated in this study.
This research was supported by Korea Agency for Infrastructure Technology Advancement grant funded by the Ministry of Land, Infrastructure and Transport (RS-2022-00141819, Development of Advanced Technology for Absolute, Relative, and Continuous Complex Positioning to Acquire Ultra-precise Digital Land Information).
Conceptualization, N.N. and K.P.; software, N.N.; validation, N.N. and K.P.; formal analysis, N.N.; methodology, N.N. and K.P.; investigation, N.N.; resources, N.N. and K.P; data curation, N.N.; writing—original draft preparation, N.N.; writing—review and editing, N.N. and K.P.; visualization, N.N. and K.P; supervision, K.P.; project administration, K.P.; funding acquisition, K.P.
The authors declare no conflict of interest.
El-Mowafy, A. 2012, Precise real-time positioning using network RTK, Global Navigation Satellite Systems – Signal, Theory and Applications, ed. S. Jin (Rijeka, Croatia: InTech), pp.161–188.
Ha, J.-H., Heo, M.-B., & Nam, G.-W. 2012, Accuracy Analysis of Precise Point Positioning Using Predicted GPS Satellite Orbits, Journal of Advanced Navigation Technology, 16, 752–759. https://doi.org/10.12673/jkoni.2012.16.5.752
Ha, J.-H., Park, K.-D., & Kim, H.-I. 2021, Available analysis of precise positioning using the LX-PPS GNSS permanent stations, Journal of Cadastre & Land Information, 51, 23–38. http://doi.org/10.22640/lxsiri.2021.51.1.23
Hofmann-Wellenhof, B., Lichtenegger, H., & Collins, J. 2001, Global Positioning System – Theory and Practice (Vienna: Springer-Verlag).
Kim, H.-I., Kim, Y.-G., & Park, K.-D. 2021, Performance Evaluation of the Low-cost, High-precision RTK Device RTAP2U for GPS-based Precise Localization, Journal of Positioning, Navigation, and Timing, 10, 67–73. https://doi.org/10.11003/JPNT.2021.10.1.67
Lee, H.-C., & Park, K.-D. 2020, Development of Code-PPP Based on Multi-GNSS Using Compact SSR of QZSS-CLAS, Journal of the Korean Society of Surveying, Geodesy, Photogrammetry and Cartography, 38, 521–531. https://doi.org/10.7848/ksgpc.2020.38.6.521
No, S.-J., Han, J.-H., & Kwon, J.-H. 2012, Accuracy Analysis of Network-RTK (VRS) for Real Time Kinematic Positioning, Journal of Korean Society of Surveying, Geodesy, Photogrammetry and Cartography, 30, 389–396. https://doi.org/10.7848/ksgpc.2012.30.4.389
Saidani, M., Sarri, P., Guinamard, A., & Maya, D. G. 2020, Virtual Base Station algorithm and performance assessment, Proceedings of the International Technical Meeting of The Institute of Navigation (ION GNSS+ 2020), online, 21–25 September 2020, pp.2696–2709. https://doi.org/10.33012/2020.17533
SBG SYSTEMS, Qinertia GNSS+INS Post-Processing Software (PPK) [Internet], cited 2025 Aug 5, available from: https://www.sbg-systems.com/softwares/qinertia-gnss-ins-ppk/