1Department of Geoinformatic Engineering, Inha University, Incheon 22212, Korea
2PP-Solution Inc., Seoul 08504, Korea
†Corresponding Author: Kwan-Dong Park, E-mail: kdpark@inha.ac.kr
Citation: Park, B.-G, & Park, K.-D, 2024, Analysis of Double-Differenced Code-Pseudorange Noise Characteristics of GNSS Receiver Combinations using Zero-Baseline Test, Journal of Positioning, Navigation, and Timing, 13, 245-256.
Journal of Positioning, Navigation, and Timing (J Position Navig Timing) 2024 September, Volume 13, Issue 3, pages 245-256. https://doi.org/10.11003/JPNT.2024.13.3.245
Received on Jul 24, 2024, Revised on Aug 04, 2024, Accepted on Aug 14, 2024, Published on Sep 15, 2024.
License: Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Following the introduction of civilian navigation, the commercial Global Navigation Satellite System (GNSS) receivers’ market has been expanding in various fields such as autonomous driving and smart cities. With improved receiver performance and widespread use of GNSS, the configurations of base and rover receivers are becoming more complex. As a result, user must consider combinations of base stations with different qualities, costs, and performances. To address these issues, we conducted zero-baseline tests to analyze the double-differenced code-pseudorange noise of various receiver combinations, ranging from low- to high-cost. The results showed that the noise varied depending on the receiver combination. Notably, receivers from the same manufacturer exhibited similar noise and positioning errors despite significant price differences. We also found that the double-differenced noise of all receiver combinations was correlated with the Carrier-to-Noise Density Ratio (C/N0), the satellite elevation angle, and the Doppler shift, and it did not perfectly follow a normal distribution. Further analysis based on Modified Allan Deviation (MDEV) showed that different types of noise were observed for each receiver combination and the double-differenced noise and positioning errors have similar statistical characteristics. From this study, the importance of receiver combinations and their various characteristics can be better understood.
GNSS, GNSS receiver, double-differenced noise, zero-baseline analysis
Global Navigation Satellite System (GNSS)이 민간용으로 도입된 이후에, 자율주행과 스마트 도시와 같은 분야에서 GNSS 수신기 시장이 확장되고 있다. 또한, 수신기 개발 기술과 성능이 향상되고 있으며, 과거부터 사용되었던 고가의 측지용 수신기에 비해 저렴한 비용을 가진 소형 단말의 공급이 증가하고 있는 추세이다 (Egea-Roca et al. 2022). 이러한 경향은 기준국-이동국 수신기 구성에도 영향을 미치고 있다. 과거에는 기준국-이동국이 고가의 측지용 수신기로 구성되었지만, 현재는 이동국에 저가의 소형 단말이 주로 사용되고 있다. 뿐만 아니라, 2024년 한국에 서비스를 시작한 Point One Navigation의 Polaris는 소형 단말 형태의 기준국을 운용하고 있다 (Inside GNSS 2024). 앞으로 사용자는 다양한 품질, 가격, 성능을 가진 기준국과의 조합을 고려해야 하는 상황에 직면할 것이고, 이용하는 기준국에 따라 이중차분 관측값과 측위의 정밀도가 달라질 것으로 보인다. 이에 대응하기 위하여, 저가에서 고가에 이르는 다양한 수신기들을 대상으로 이중차분 잡음과 측위 오차 특성을 분석할 필요성이 있다.
관측값의 이중차분 잡음 분석을 위해서, 수신기의 안테나간 기선거리를 0으로 만들어 공통오차를 소거하는 영기선 분석을 주로 수행한다. Kersten & Paffenholz (2020)은 u-blox M8T, Septentrio PolaRx5, Javad TRE-G3T 그리고 Leica GRX1200+ 수신기를 사용하여 Global Positioning System (GPS) L1과 GLObal NAvigation Sateliite System (GLONASS) G1을 대상으로 영기선 분석을 수행하였다. 해당 연구에서는 저가의 수신기인 u-blox M8T 2개를 기준국-이동국으로 사용함으로써, 고가의 측지용 수신기와 조합을 이루는 것에 비해 이중차분 잡음의 Root Mean Squares (RMS)를 코드 의사거리에서 약 0.8 m, 반송파 위상에서 약 0.1 mm를 줄일 수 있음을 보였다.
수신기 조합별로 이중차분 잡음을 비교하는 것보다 잡음의 유형을 특정하는 하는 것에 초점을 맞춘 연구는 Prochniewicz et al. (2022)이 있다. 해당 연구에서는 2개의 Trimble NetR9으로 GPS, GLONASS, Galileo 항법위성군의 L1, L2, L5 대역 신호를 취득하여 영기선 분석을 수행하였다. 해당 연구의 분석 과정에서는 코드 의사거리와 반송파 위상의 이중차분 잡음이 어떤 잡음인지 특정하기 위해 Modified Allan Deviation (MDEV)을 활용하였다. 분석 결과에 따르면, 코드의사거리는 모든 항법위성군에서 Flicker Phase Modulation (FPM)이나 White Phase Modulation (WPM)으로 특징지어졌으며, GPS, Galileo의 반송파 위상은 WPM의 잡음 형태를 가지고 있고, GLONASS는 FPM과 WPM으로 특징지을 수 있음을 보였다.
잡음 유형 분석 방식을 측위 오차에 적용한 연구는 Niu et al. (2014)이 있다. 해당 연구에서는 Trimble NetR8과 NetR9으로 GPS 신호를 취득하여 Standard Point Positioning (SPP), Precise Point Positioning (PPP), Differential GPS (DGPS)의 측위 오차를 잡음으로 모델링하고자 하였다. 모델링을 위해 측위 오차의 Allan Variance (AVAR)를 계산하였고, SPP, PPP, DGPS 측위 오차의 남북방향 (N), 동서방향 (E), 수직방향 (V) 성분에 1st Order Gauss-Markov process, White Noise (WN), random walk noise, 그리고 flicker noise가 지배적으로 나타남을 보였다. 해당 연구는 GPS 측위 오차가 WN뿐만 아니라 다양한 잡음과 함께 모델링됨으로써, 오차 분석과 측위 성능 향상에 기여할 수 있을 것으로 보았다.
앞서 기술한 선행 연구들은 수신기 조합별 이중차분 잡음 비교, 이중차분 잡음과 측위 오차의 잡음 유형 분석으로 구분할 수 있다. 기존의 연구들은 항법위성군과 수신기 조합에 따르는 이중차분 잡음과 측위 오차의 크기, 잡음의 유형이 종합적으로 분석되지 않았으며, Carrier to Noise Density Ratio (C/N0), 도플러 천이 그리고 관측 위성의 고도각과의 관계에 대한 분석이 부족하다. 또한, AVAR은 WPM에서 FPM를 분리하지 못하는 단점이 있어 잡음의 유형을 구체적으로 분석하기 위해서는 AVAR보다 MDEV를 도입하는 것이 용이하다 (Allan & Barnes 1981).
코드 의사거리는 반송파 위상에 비해 잡음이 크지만 모호성이 없는 반면, 반송파 위상은 잡음의 크기가 작지만 모호성을 가지고 있는 관측이다 (Misra & Enge 2006). 이러한 이유로 코드의사거리를 이용한 이중차분 측위에서는 잡음의 크기가 측위 정밀도 측면에 지배적인 영향을 미칠 수 있다. 따라서, 코드의사거리 이중차분 잡음의 특성과 유형을 분석하고, 측위 오차에서 어떠한 형태로 발현되는 지 확인할 필요성이 있다. 하지만, 국내에서는 이러한 연구 사례가 부족한 실정이다.
따라서, 이 연구에서는 저가에서 고가에 달하는 다양한 수신기 조합을 구성하여 코드의사거리 관측값의 잡음 특성과 유형을 비교 분석하고, 측위 오차와의 연관성을 탐색한다. 우선, 선행 연구에 사용되지 않았던 Septentrio SB3 PRO+ (SB3), mosaic-X5 (MX5), Javad TRE-3S (TRE), u-blox ZED-F9P (F9P)를 사용하여 선행연구들과 같은 GNSS 수신기 기술분야의 연구결과를 확장하고자 한다. 그리고, GPS L1, GLONASS G1, Galileo E1의 코드 의사거리 이중차분 잡음을 집중적으로 다루어 여러 항법위성군의 코드의사거리에 대한 종합적인 분석결과를 제시하고자 한다. 또한, 추가적으로 측위 오차와의 관계성을 분석함으로써, 측위 오차와 이중차분 잡음이 분리되어 분석되었던 선행연구들보다 심층적인 분석 결과를 보이고자 한다.
이 연구의 2장에서는 실험의 구성과 취득 데이터의 후처리 대하여 설명한다. 3장에서는 영기선 이중차분 잡음 도출에 관한 이론적 배경을 기술하고, 4장에서는 이중차분 잡음과 측위 오차의 RMS를 통해 최적의 기준국-이동국 수신기 조합을 분석한다. 5장에서는 C/N0, 관측 위성의 고도각, 도플러 천이와 이중차분 잡음의 상관성을 분석한다. 또한, 정규확률 그래프 그리고 MDEV를 활용하여 통계적 분석을 수행한다. 마지막으로 6장에서는 분석 결과에 대한 논의와 함께 향후 연구 계획과 방향에 대하여 기술한다.
이번 장에서는 영기선 테스트를 통한 데이터 취득과 데이터의 후처리 과정을 기술한다. 2.1절에서는 테스트에 사용한 안테나와 수신기 구성을 설명하고, 2.2절에 데이터 후처리 과정에 대하여 기술한다.
영기선 분석을 위해 2024년 1월 14일 인하대학교 4호관 옥상 안테나를 통해 GPS L1, Galileo E1, GLONASS G1의 코드의사거리를 24시간 동안 1초 간격으로 취득하였고, 수신기 안테나간 기선거리를 0으로 설계하기 위하여 하나의 안테나에서 취득한 신호를 스플리터로 분배하였다. 구체적인 실험의 구성은 Fig. 1에 나타내었다.
데이터 취득에 사용한 안테나는 Tallysman VC6510이며 Fig. 1a의 A에 해당한다. Fig. 1b를 통해서 확인할 수 있듯이 안테나에서 수집한 신호는 Tallysman TW165 스플리터를 통해 SB3, MX5, TRE, F9P로 분배된다. SB3와 TRE는 천 만원에 달하는 가격대를 형성하고 있고, 이에 반해 MX5, F9P는 수 십에서 1~2백만원 수준으로 상대적으로 저가이며, 소형 단말에 해당한다. 고가형 수신기와 저가형 수신기를 함께 실험에 사용함으로써 고가의 기준국 수신기와 저가의 사용자 수신기간의 상대 측위 시나리오를 모의 실험할 수 있고, 4가지 수신기에서 발생할 수 있는 6가지 조합을 대상으로 영기선 분석이 가능하다. Table 1에 수신기별 채널 수를 표기하였으며, 수신기 약어는 가독성 향상을 목적으로 편의에 따라 정리하였다.
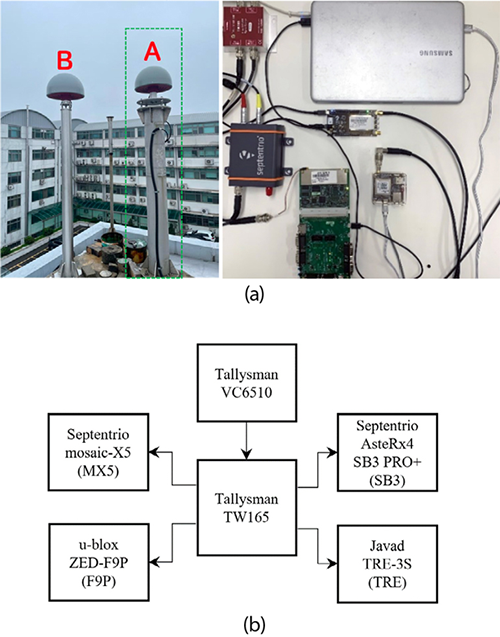
Fig. 1. Configuration of zero-baseline test, (a) antenna and receiver, (b) block diagram for signal path from antenna to receiver.
Table 1에서 확인할 수 있듯이 F9P가 물리적인 채널의 수가 가장 적다. 이는, F9P가 다른 수신기에 비해 취득되는 위성군의 수가 많지 않다는 것을 나타낸다. 이 연구의 실험에서 F9P를 통해 취득한 BeiDou의 위성 수가 다른 수신기들에 비해 적게 나타났다. 따라서, 다른 항법위성군에 비해 신호의 양이 분석을 수행하는데 충분하지 않다고 판단하여 이 논문의 분석에서는 제외하였다.
Table 1. Number of available hardware channels of zero baseline receiver.
| Receiver | # of channel |
|---|---|
| Septentrio AsteRx4 SB3 PRO+ (SB3) | 544 |
| Javad TRE-3S (TRE) | 874 |
| Septentrio mosaic-X5 (MX5) | 448 |
| u-blox ZED-F9P (F9P) | 184 |
이 연구에서는 Kawamoto et al. (2023)의 RINGO 소프트웨어를 사용하여 1초 간격의 관측값을 5초 간격으로 편집하였다. 취득 데이터의 해상도를 5초 간격으로 줄임으로써 대용량 처리 속도를 줄일 수 있으며, 이 연구에서 분석하고자 하는 이중차분 잡음의 특성도 상실되지 않는다. 또한, 매 시점마다 모든 수신기의 공통위성들의 관측값을 추출하여 정확한 비교 분석이 이루어질 수 있도록 하였다.
이번 장에서는 영기선 코드의사거리 관측값의 이중차분 잡음 도출에 필요한 이론적 배경을 기술한다. 영기선 관측을 통해 임의의 시점 $t$에서 취득한 위성의 코드 의사거리 $\rho_r^s(t)$는 Eq. (1)과 같이 수신기와 위성간 3 차원 기하거리 $r_r^s(t)$와 추가적인 오차 항으로 구성되어 있다.
$$\rho_r^s(t) = r_r^s(t) + c[\delta t_r(t) – \delta t^s(t – \tau) + \delta_r(t) – \delta^s(t)]
+ \delta I_r^s(t) + \delta T_r^s(t) + \delta M_r^s(t) + \epsilon_\rho(t) \, [\text{m}]$$
Misra & Enge (2006), Kaplan & Hegarty (2006), Hofmann-Wellenhof et al. (2008)에 의하면, $c$는 빛의 속도를 의미하며, 수신기 시계오차 $\delta t_r(t)$은 GPS Time (GPST)와 수신기에 탑재된 시계 간의 시간 차이를 나타낸다. 위성 시계오차 $\delta t^s(t-\tau)$은 GPST와 위성에 탑재된 시계 간의 시간 차이에 해당하고, $\tau$는 신호전달시간을 의미한다. 수신기 하드웨어 바이어스 $\delta _r$은 신호가 안테나 위상 중심에서 취득되고 코드의사거리가 생성되기까지의 시간을 나타내며, 위성 하드웨어 바이어스 $\delta _s$는 신호가 위성 하드웨어에서 생성되고 방사되기까지의 시간을 의미한다. 이온층 오차 $\delta I_r^s(t)$와 대류권 오차 $\delta S_r^s(t)$는 신호가 대기를 통과하면서 굴절하여 발생하는 오차이다. 다중경로 오차 $\delta M_r^s(t)$는 신호가 대기를 통과해 지상에 도달할 때 장애물, 지형 지물 등에 의해 산란되거나 반사되어 발생하는 오차이다. $\epsilon_\rho(t)$은 일반적으로, 유선 상에서 발생하는 열 잡음을 의미하며, 세부적으로는 하드웨어 구성 등에 의해 발생하는 관측값 오차를 포함한다.
영기선 코드 의사거리의 차분을 수행하기 위하여 매 시점 t마다 관측 위성들 중에서 고도각이 가장 높은 위성을 선택하여 차분의 기준으로 정한다. Pivot Satellite (PS)와 Other Satellite (OS)에 대하여 앞서 기술한 Eq. (1)의 수신기간 단일 차분을 수행하면 Eqs. (2, 3)을 도출할 수 있다.
$$\rho_{r_1, r_2}^P(t) = c[\delta t_{r_1, r_2}(t) + \delta_{r_1, r_2}(t)] + \epsilon_{r_1, r_2}^P(t) \, [\text{m}]$$
$$\rho_{r_1, r_2}^0(t) = c[\delta t_{r_1, r_2}(t) + \delta_{r_1, r_2}(t)] + \epsilon_{r_1, r_2}^0(t) \, [\text{m}]$$
여기서 $\rho_{r_1, r_2}^P(t)$과 $\rho_{r_1, r_2}^0(t)$는 시점 t에서의 PS와 OS의 수신기간 단일 차분 결과이다. 수신기간 단일 차분을 통해 위성시계오차 $\delta t^s(t-\tau)$, 위성 하드웨어 바이어스 $\delta ^s(t)$가 소거되고, 수신기 안테나 간의 기선거리가 0이기 때문에 수신기와 위성간 3차원 기하거리 $r_r^s(t)$, 이온층 오차 $\delta I_r^s(t)$와 대류권 오차 $\delta T_r^s(t)$, 다중경로 오차 $\delta M_r^P(t)$가 소거된다. 두 수신기의 시계가 동일하지 않으며, 내부 하드웨어 구성이 달라 하드웨어 바이어스의 양이 다르기 때문에 단일 차분을 통해서 소거되지 않는 오차는 수신기 시계오차, 수신기 시계 바이어스, 잡음이다. 또한, 일반적으로 유선 상에서 발생하는 열잡음은 평균이 0인 정규 분포를 따르기 때문에 덧셈이나 뺄셈을 수행함으로써 그 분산이 변할 수 있지만 사라지지는 않는다. 따라서, 수신기간 단일 차분에 따라 잔여하는 오차는 두 수신기 시계오차의 차이 $\delta t_{r_1, r_2}(t)$, 두 수신기의 하드웨어 바이어스 차이 $\delta _{r_1, r_2}(t)$, 단일 차분 잡음 $\epsilon_{r_1, r_2}(t)$이 된다.
마지막으로, Eqs. (2, 3)를 차분 하면, Eq. (4)의 영기선 이중차분 잡음을 도출할 수 있다.
$$\rho_{r_1, r_2}^{P, 0}(t) = \epsilon_{r_1, r_2}^{P, 0}(t) \equiv \nabla \Delta \epsilon(t) \, [\text{m}]$$
여기서 $\rho_{r_1, r_2}^{P, 0}(t)$는 시점 t에서의 이중차분 결과이다. Eqs. (2, 3)의 차분을 통해 시계오차의 차이 $\delta t_{r_1, r_2}(t)$, 수신기 하드웨어 바이어스의 차이 $\delta _{r_1, r_2}(t)$가 소거되지만, 단일 차분 잡음 $\epsilon_{r_1, r_2}^P(t)$는 소거되지 않고 이중차분 잡음 $\epsilon_{r_1, r_2}^{P,O}(t)$로 남아있다. 분석에 사용될 이중차분 잡음은 편의상 $\nabla \Delta \epsilon(t)$로 표기하였다.
이번 장에서는 최적의 수신기 조합을 판단하기 위하여 이중차분 잡음과 측위 오차의 RMS를 비교한다. 4.1절에서는 코드의사거리 관측값의 이중차분 잡음의 RMS를 통해 6가지의 수신기 조합을 평가하고, 4.2절에서는 수신기 조합들의 코드의사거리 이중차분 측위 오차의 RMS를 비교하였다.
이 연구에 사용한 네 개의 수신기가 가질 수 있는 기준국–이동국 조합은 총 6개이다. 모든 항법 시스템으로부터 취득한 관측값의 이중차분 RMS 잡음은 Fig. 2와 Table 2를 따른다.
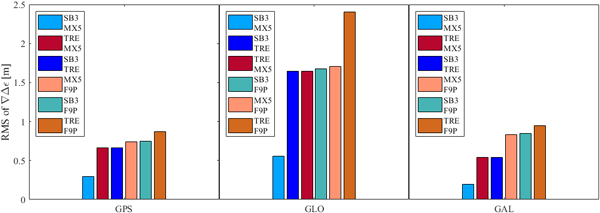
Fig. 2. RMS of double differenced noise of GPS, GLONASS, Galileo for each receiver combination.
Table 2. RMS value of double differenced noise of GPS, GLONASS, Galileo for each receiver combination.
| System | RMS of each receiver combination [m] | |||||
|---|---|---|---|---|---|---|
| SB3 – TRE | SB3 – MX5 | SB3 – F9P | TRE – MX5 | TRE – F9P | MX5 – F9P | |
| GPS | 0.667 | 0.295 | 0.748 | 0.666 | 0.872 | 0.739 |
| Galileo | 0.541 | 0.197 | 0.847 | 0.540 | 0.950 | 0.836 |
| GLONASS | 1.420 | 0.440 | 1.509 | 1.424 | 2.195 | 1.510 |
Fig. 2와 Table 2를 통해서 확인할 수 있듯이, 모든 항법 위성군에서 SB3-MX5의 이중차분 잡음이 가장 작게 나타났다. Kersten & Paffenholz (2020)의 연구에서는 동일한 수신기를 사용하여 잡음의 크기가 작아질 수 있음을 보였지만, 이 연구에서는 같은 제조사의 이기종 수신기를 조합할 경우에도 높은 관측 정밀도를 얻을 수 있음을 확인하였다. 또한, SB3-TRE, TRE-MX5는 1 cm 이내의 차이를 보였으며, SB3-F9P, MX5-F9P는 GPS, Galileo에서 약 1 cm, GLONASS에서 0.1 cm 수준의 작은 차이를 보였다. 이를 통해서 같은 제조사의 제품들은 다른 수신기들과 조합하여도 유사한 잡음 크기를 보인다는 것을 확인하였다.
측위 오차 부분에서도 4.1절의 분석이 유효한지 확인하기 위하여 영기선 이중차분 측위를 수행하였다. GPS, Galileo의 위성 좌표는 케플러 궤도 요소를 이용하여 계산하였으며, GLONASS의 궤도 계산에는 Runge-Kutta 4차 수치적분을 이용하였다. 이중차분 잡음에 의한 측위 오차 분석을 수행하기 위하여 고도각과 C/ N0에 따른 가중치 적용은 하지 않았으며, 관측의 정밀도만으로 얻을 수 있는 오차를 얻고자 최소제곱추정을 사용하였다. 확장형 칼만필터를 이용하여 위치 추정을 수행할 수 있지만, 필터의 파라미터에 따라 측위 오차가 달라질 수 있다는 점이 이번 분석의 목적에 부합하지 않기 때문에 확장형 칼만 필터를 사용하지 않았다. 영기선 측위의 수평오차 (dH), 수직오차 (dV)를 Figs. 3-4와 Table 3에 정리하였다.
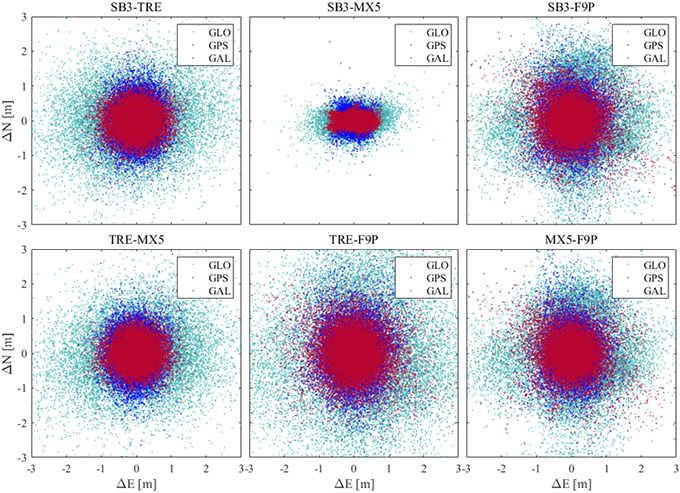
Fig. 3. Horizontal error of relative positioning using double-differenced code-pseudorange of GPS L1, GLONASS G1, Galileo E1.
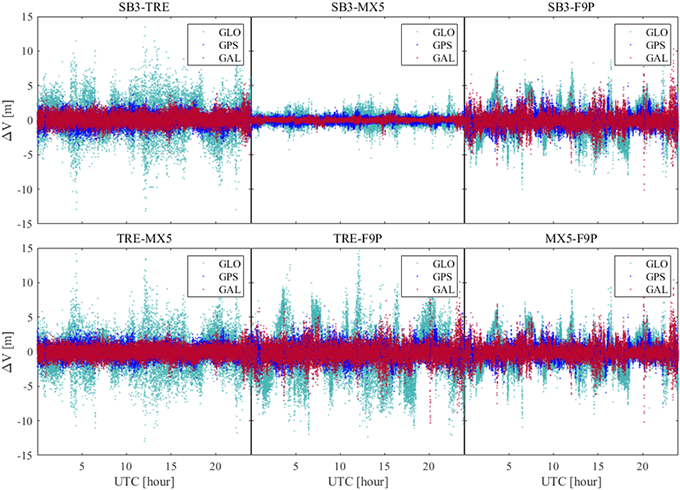
Fig. 4. Vertical error of relative positioning using double-differenced code-pseudorange of GPS L1, GLONASS G1, Galileo E1.
Table 3. Double differenced code-pseudorange noise and positioning RMS [m].
| Receiver combination | GPS | GLONASS | Galileo | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ∇Δε | dH | dV | ∇Δε | dH | dV | ∇Δε | dH | dV | |
| SB3-TRE | 0.667 | 0.610 | 0.870 | 1.420 | 1.379 | 2.446 | 0.514 | 0.540 | 0.799 |
| SB3-MX5 | 0.295 | 0.273 | 0.342 | 0.440 | 0.477 | 0.696 | 0.197 | 0.251 | 0.245 |
| SB3-F9P | 0.748 | 0.685 | 1.000 | 1.509 | 1.469 | 2.383 | 0.847 | 0.747 | 1.222 |
| TRE-MX5 | 0.666 | 0.609 | 0.862 | 1.424 | 1.388 | 2.439 | 0.540 | 0.531 | 0.801 |
| TRE-F9P | 0.872 | 0.789 | 1.152 | 2.195 | 2.134 | 3.631 | 0.950 | 0.849 | 1.388 |
| MX5-F9P | 0.739 | 0.671 | 0.976 | 1.510 | 1.462 | 2.396 | 0.836 | 0.734 | 1.203 |
Figs. 3-4와 Table 3에서 알 수 있듯이, 모든 항법 위성군에서 SB3-MX5가 가장 작은 수평 오차와 수직 오차를 보이고 있으며, TRE-F9P에서 가장 큰 오차가 나타나고 있다. 이를 통해서, 같은 제조사의 제품군으로 기준국-이동국을 구성하면, 이중차분 잡음의 크기가 작아지고, 측위 정밀도가 상승한다는 것을 확인하였다. 또한, SB3-TRE, TRE-MX5 그리고 SB3-F9P, MX5-F9P는 측위 오차의 차이가 각각 1 cm 수준으로 나타났으며, 수평 방향과 수직 방향 오차의 패턴이 비슷한 것으로 나타났다. 이를 통해서 같은 제조사의 수신기 기종은 다른 수신기와 조합하였을 때, 측위 오차 특성이 유사할 수 있음을 확인하였다.
이번 장에서는 6가지 수신기 조합의 이중차분 잡음 특성을 분석한다. 5.1절에서는 C/N0, 관측 위성의 고도각, 도플러 천이에 따른 이중차분 잡음 분석을 수행하고, 5.2 ~ 5.4절에서는 이중차분 잡음의 정규성을 평가하고, MDEV를 이용한 시계열 통계분석을 수행하였다. 또한, 이중차분 잡음과 측위 오차의 통계적인 특성을 비교 분석하였다.
수신기 조합마다 이중차분 잡음의 RMS는 다르지만 C/N0, 관측 위성의 고도각, 도플러 천이의 크기에 따라서 시계열 잡음에서 볼 수 없던 특징을 발견할 수 있다. 따라서, Figs. 5-8에 관측된 모든 공통 위성들의 이중차분 잡음을 시계열, C/N0, 관측위성의 고도각, 도플러 천이에 따라 나타내었다.
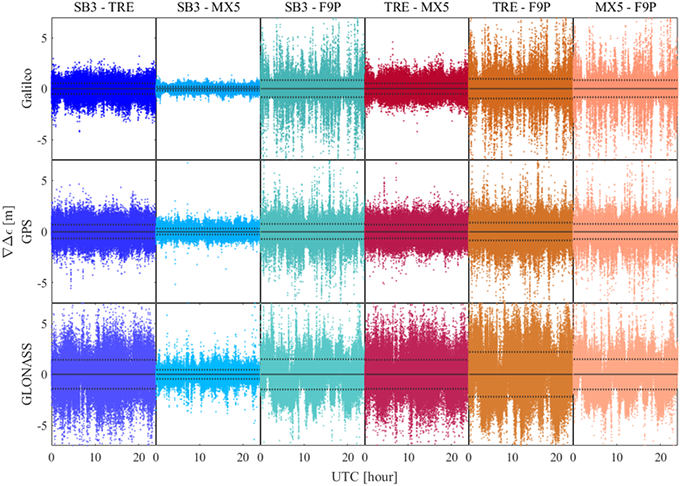
Fig. 5. Time series double-differenced code-pseudorange noise.
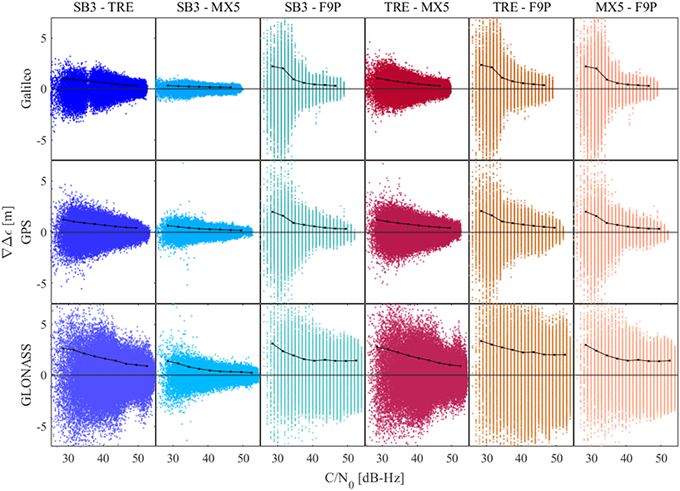
Fig. 6. Comparison plot of correlation of code-pseudorange double-differenced noise with respect to C/N0.
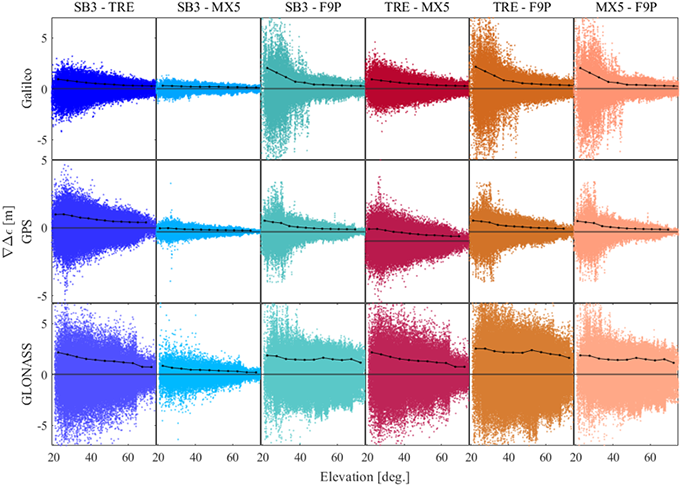
Fig. 7. Comparison plot of correlation of code-pseudorange double-differenced noise with respect to elevation.
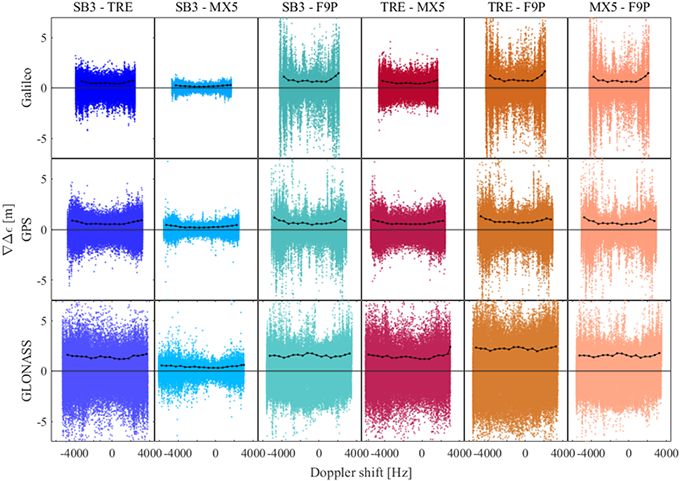
Fig. 8. Comparison plot of correlation of code-pseudorange double-differenced noise with respect to doppler shift between receiver and OS.
Fig. 5의 점선은 ±RMS를 나타내며, Figs. 6-8에는 C/N0 3 dBHz, 고도각 10도, 도플러 천이 500 Hz 간격의 RMS를 검정색 실선으로 표시하였다. Fig. 5에 나타낸 수신기 조합 중, SB3-F9P, TRE-F9P, MX5-F9P는 다른 조합에 비해 잡음이 시간에 따라 큰 폭으로 변하는 특성이 있다. 일반적으로, C/N0가 낮아진다는 것은 신호의 전력에 비해 잡음의 전력이 상대적으로 커진다는 것을 나타내며, 관측 위성의 고도각이 낮아지는 것은 신호 전달거리가 길어지면서 거리에 따른 신호 감쇄가 커지는 것을 의미한다.
Figs. 6-7을 통해서, 크기가 큰 잡음들은 낮은 C/N0과 관측 위성의 고도각에서 나타났으며, 수신기 조합에 따라 이중차분 잡음의 패턴이 유사함을 알 수 있다. SB3-TRE, SB3-MX5, TRE-MX5는 전체 항법위성군의 C/N0과 고도각이 낮아지면서 잡음의 분산이 일정하게 감소하는 패턴을 보이지만, GPS, Galileo의 SB3-F9P, TRE-F9P, MX5-F9P는 C/N0 약 35 dB-Hz, 고도각 약 40도 부근부터 잡음의 분산이 급격하게 증가하는 형태를 보이고 있다.
관측 위성과 수신기간의 상대속도에 의해 발생하는 도플러 천이에 따른 이중차분 잡음의 패턴은 Fig. 8과 같다. 측정된 도플러 천이의 범위가 항법 시스템별로 다르게 나타난다. GLONASS는 19,100 km, GPS는 20,200 km, Galileo는 23,222 km의 고도를 가지고 있어 위성의 운동 속도가 GLONASS, GPS, Galileo 순으로 빠르기 때문이다. 따라서, 도플러 천이의 범위는 GLONASS, GPS, Galileo 순으로 넓다. 모든 항법위성군에서 도플러 천이는 C/N0과 관측 위성의 고도각에 비해 뚜렷하지 않다. Fig. 8에 나타낸 것과 같이 도플러 천이가 높아질수록 크기가 큰 잡음이 주로 관측되지만, 도플러 천이가 낮음에도 불구하고 큰 잡음이 관측되는 경향이 있다.
Figs. 6-8에서 확인할 수 있듯이, C/N0, 도플러 천이, 관측위성의 고도각은 이중차분 잡음과 상관성을 보이고 있다. 하지만, 낮은 C/N0과 고도각에서도 작은 크기의 잡음들이 관측되고 있다. 따라서, 6가지 수신기 조합이 어떠한 분포를 가지고 있는지 분석한다.
일반적으로, GNSS 수신기의 잡음은 정규 분포를 따른다고 가정한다. 정규 분포는 덧셈이나 뺄셈을 수행하여도 정규 분포를 따르기 때문에 이중차분 잡음도 정규 분포를 따른다. 따라서, 분석에 사용한 수신기 조합이 이러한 가정에 부합하는지 확인하기 위하여 정규확률 그래프를 Fig. 9에 나타내었다.
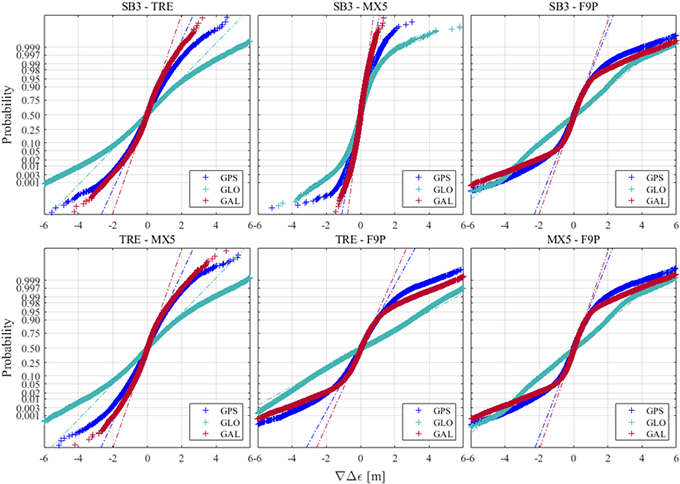
Fig. 9. Normal probability plot of double-differenced code-pseudorange noise GPS, GLONASS, Galileo for each combination of receivers.
정규확률 그래프는 표본 데이터의 분위 수를 정규 분포의 분위 수와 일치시켜 표본의 정규성을 나타낸다. 파선부분은 정규 분포의 1분위 수와 3분위 수의 연장선이다. 따라서, ‘+’로 도시한 이중차분 잡음들이 파선을 따라 분포하면 정규 분포를 만족하고, 심볼이 곡선으로 분포하면 정규분포를 만족하지 않는다. 모든 수신기 조합 중, GLONASS의 SB3-F9P, TRE-F9P, MX5-F9P가 이중차분 잡음이 정규성을 만족하고 있다. 또한, Galileo의 SB3-MX5는 약 99%가 정규성을 만족하고 있다. 이들을 제외한 나머지 조합들은 약 80%가 정규성을 만족하고 있으며, 이중차분 잡음의 크기가 커지면서 정규분포와 멀어지고 있다. 정규성을 만족하지 않는 잡음들은 약 1.5 m ~ 6 m의 크기를 가지고 있는데, 이러한 잡음들은 고도각과 C/N0이 낮거나 도플러 천이가 높을 경우에 발생하는 것임을 Figs. 6-8을 통해 확인할 수 있다.
분석에 사용한 일부 수신기 조합은 정규분포를 따르지만, 그렇지 않은 조합들도 있다. 이는, 이상값에 의한 영향이라고 볼 수도 있지만, 다른 유형의 잡음의 영향일 가능성도 존재한다. 따라서, 구체적인 잡음의 유형을 판독하기 위하여 MDEV를 도입하였다.
MDEV는 시계 또는 주파수 안정성을 평가하기 위해 사용되는 통계적 분석 방식으로, 임의의 시계열 신호 샘플의 시간지연에 따른 주파수 변동을 계산한다. Allan & Barnes (1981)에 따르는 MDEV는 Eq. (5)와 같다.
$$\text{mod} \, \sigma_y(\tau) = \sqrt{\frac{1}{2\tau^2} \left[ \frac{1}{n} \sum_{i=0}^{n-1} x_{i+2n} – 2x_{i+n} + x_i \right]^2}$$
여기서 MDEV $\text{mod} \, \sigma_y(\tau)$는 시간 지연 $\tau$를 늘려가며 주파수 $x_i$의 차이의 평균을 계산하고, 제곱한 뒤에 $2\tau ^2$로 정규화하고 제곱근을 취해 계산할 수 있다. 계산된 MDEV의 기울기를 통해서 짧은 시간 동안에 신호에 영향을 미치는 잡음의 특성을 알 수 있다.
Riley & Howe (2008)에 의하면 잡음의 종류를 파악하기 위해서는 MDEV의 기울기가 Table 4를 따라야 한다.
Table 4. Noise type and corresponding slope of MDEV.
| Slope of MDEV | ||||||
|---|---|---|---|---|---|---|
| White PM | Flicker PM | White FM | Flicker FM | RWFM | Freq. Drift | |
| τ-3/2 | τ-2/2 | τ-1/2 | τ0 | τ1/2 | τ2/2 | |
Riley & Howe (2008)에 의하면, MDEV의 기울기에 따라서 크게 6가지 형태로 잡음을 특정할 수 있다. White PM은 신호의 위상에 영향을 주는 고주파 잡음으로, 모든 주파수 대역에서 평탄한 잡음 밀도를 가진다. FPM은 주파수가 낮을수록 잡음 전력이 증가하는 특성을 가지고 있어, 신호의 저주파 대역에 영향을 미친다. White Frequency Modulation (WFM)은 WPM과 같이 고주파 잡음의 일종으로, 주파수의 무작위 변동을 발생시킨다. Flicker Frequency Modulation (FFM)은 FPM과 같이 저주파 잡음의 일종으로, 주파수의 변동을 일으켜 주파수의 일관성을 저하시킨다. Random Walk Frequency Modulation (RWFM)은 주파수가 시간이 지남에 따라 무작위로 변동하는 특성이 있으며, 주로 저주파 대역에 집중되어 있다. Freq. Drift (FD)는 주파수가 시간에 따라 서서히 변동하는 특성을 가지고 있으며, 장기적인 시간 스케일에서 관측할 수 있다.
이번 분석에서는 MDEV를 개별 위성 관측값의 이중차분 잡음에 적용하여 시간에 따른 주파수의 변동이 아닌 이중차분 잡음의 변동을 계산한다. 또한, 계산된 평균 MDEV의 기울기를 통해 분석에 사용한 항법위성군과 수신기 조합에 나타나는 잡음의 종류를 확인한다. 이때, IEEE (1998)에 따라 임의의 시간지연에서 개별 잡음 프로세스가 독립적으로 동시에 영향을 줄 수 있다고 가정한다. 각 수신기 조합별 평균 MDEV는 Fig. 10과 같다.
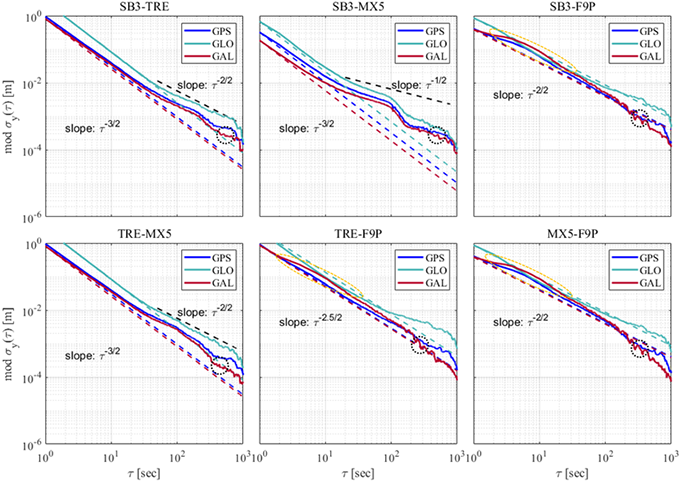
Fig. 10. Average MDEV of GPS, GLONASS, Galileo for double difference code-pseudorange noise.
Fig. 10에 나타낸 실선은 관측 위성의 평균 MDEV이며, 점선은 초기 지연 시간 동안 가장 적합하다고 판단되는 기울기를 나타낸 것이다. 앞서 수신기 조합별로 이중차분 잡음의 RMS를 비교 분석한 결과에 따르면, 같은 제조사의 수신기들은 다른 수신기와 조합하였을 때 잡음의 크기가 유사하게 나타났다. 이와 유사한 결과로써, 같은 제조사의 수신기들은 잡음의 유형도 유사함을 Fig. 10에서 확인할 수 있다. SB3-F9P, MX5-F9P는 전반적으로 FPM을 따르고 있으며, SB3-TRE, TRE-MX5는 WPM이 주로 나타나고 있다. SB3-MX5는 초기에 WPM을 따르다가 시간이 지남에 따라 WFM의 형태를 가지고 있다. TRE-F9P는 전반적으로 $\tau ^{-2.5/2}$를 따르고 있으며, WPM과 FPM이 동시에 영향을 주고 있을 것으로 예상하였다. 하지만, RWFM과 FD는 이 연구에 사용한 수신기 조합에서는 발견되지 않았다.
WPM, FPM, WFM 외에도 발견되는 잡음의 형태는 Fig. 10에 주황색과 검정색으로 표기하였다. SB3-F9P, TRE-F9P, MX5-F9P는 초기 지연 시간 구간에서 기울기가 변했다가 지연 시간 100초 이후에 다시 돌아오는 패턴이 모든 항법위성군에서 나타난다. 뿐만 아니라, SB3-MX5는 기울기가 100초 부근에서 기울기가 감소하다가 $\tau ^{-1/2}$로 다시 증가하는 패턴이 발생하였고, TRE-MX5의 GPS, Galileo MDEV의 100초 근방에서도 나타난다. IEEE (1998)에 따르면 이러한 형태의 잡음은 Correlated Markov Noise (CMN)이다. 또한, 모든 수신기 조합의 MDEV는 시간 지연이 1000초에 가까워지면서 진동하는 Sinusoidal Noise (SN) 형태의 잡음이 동시에 관측된다.
영기선 측위 오차가 이중차분 잡음과 어떠한 통계적 특성을 공유하고 있는지 확인하기 위하여 앞서 수행하였던 MDEV를 이용한 분석을 도입한다. 수평 방향과 수직 방향 오차 성분의 평균 MDEV를 계산하고, 이중차분 잡음의 평균 MDEV를 비교한 결과를 Fig. 11에 나타내었다.
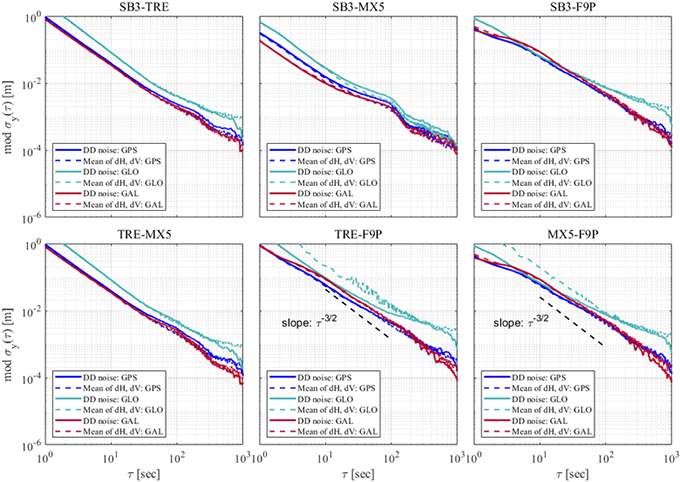
Fig. 11. Average MDEV of double-differenced code-pseudorange noise and positioning error (mean of dH, dV) of GPS L1, GLONASS G1, Galileo E1.
실선은 이중차분 잡음의 평균 MDEV를 나타내며 점선은 영기선 측위의 수평 방향과 수직 방향 오차의 평균 MDEV이다. Fig. 11에서 확인할 수 있듯이, 같은 제조사의 수신기들은 다른 제조사의 수신기와 조합하였을 때, 측위 오차의 통계적 특성도 비슷한 것으로 나타났다. SB3-F9P, MX5-F9P의 GPS와 Galileo는 측위 오차의 평균 MDEV가 유사하며, SB3-TRE, TRE-MX5는 모든 항법위성군에서 동일한 패턴을 보이고 있다.
또한, TRE-F9P, MX5-F9P의 GLONASS를 제외한 모든 조합에서 영기선 이중차분 잡음과 측위 오차가 유사한 특성을 보였다. 이는, 수평방향과 수직방향 오차의 평균은 이중차분 잡음과 같은 유형의 잡음으로 분류할 수 있다는 것을 의미한다. SB3-F9P, MX5-F9P의 측위 오차는 FPM을 따르고 있으며, SB3-TRE, TRE-MX5는 WPM의 형태로 나타났다. SB3-MX5은 WPM, WFM의 영향이 측위 오차에 동시에 나타나고 있으며, TRE-F9P는 WPM, FPM에 동시에 영향을 받는 특성을 보인다. 추가적으로, 이중차분 잡음에서 나타난 CMN과 SN도 측위 오차의 평균 MDEV에 나타나고 있다.
초기 지연시간동안 이중차분 잡음과 측위오차의 평균 MDEV가 일치하지 않는 조합도 존재한다. GLONASS에서 MX5-F9P는 이중차분 잡음이 FPM을 따르지만, 측위 오차는 WPM을 따르고 있다. TRE-F9P의 이중차분 잡음은 WPM과 FPM이 동시에 영향을 주는 형태였지만, 측위 오차는 WPM에 가까운 것으로 나타났다. 하지만, 지연시간이 길어지면서, 평균 MDEV가 유사해진다.
이 연구는 RTK, N-RTK의 기준국-이동국 수신기 구성이 다양해짐에 따라 발생할 수 있는 코드의사거리 관측값과 측위의 정밀도 차이를 비교하고 이중차분 잡음의 특성을 분석하기 위한 목적으로 수행되었다. 수신기 조합에 따른 비교를 위해서 Septentrio SB3 PRO+, mosaic-X5, Javad TRE-3S, u-blox ZED-F9P를 사용하여 GPS L1, GLONASS G1, Galileo E1의 코드의사거리 관측값에 대한 영기선 분석을 수행하였다.
분석 결과, 모든 항법위성군의 코드 의사거리 영기선 이중차분 잡음과 측위 오차의 RMS는 같은 제조사의 수신기 조합에서 가장 작았으며, GPS L1, Galileo E1, GLONASS G1에서 각각 0.295 m, 0.197 m, 0.440 m로 나타났다. 또한, 측위 오차의 수평 방향 성분의 RMS는 잡음의 RMS와 높은 연관성이 있음을 확인하였다. 수신기 조합에 따라 이중차분 잡음의 정밀도는 다르지만, 공통적으로 C/N0, 관측 위성의 고도각, 도플러 천이와 상관성을 가지고 있었으며, 잡음의 크기가 큰 관측들은 정규분포를 따르지 않는 것으로 나타났다. 뿐만 아니라, 모든 항법 위성군과 수신기 조합에 걸쳐 이중차분 잡음과 수평 방향과 수직 방향 측위 오차의 평균이 WPM, FPM, WFM, CMN, SN으로 구성됨을 확인하였다.
이전 연구들과 유사하게, 코드의사거리 이중차분 잡음은 WPM, FPM, WFM이 주로 나타났지만, 특정 조합에서는 FPM과 WFM의 영향이 동시에 있을 수 있는 유형이 관측되었다는 것에 차이가 있다. 이는, 수신기 조합에 따라 발생할 수 있는 잡음 유형이 다양하다는 것을 의미한다. 또한, CMN과 SN이 발견되었다는 것에서도 이전연구와 차이가 있다. 이러한 잡음이 외부환경에 의해서 발생된 것인지, 수신기 조합의 고유한 특성인지는 다양한 경우들을 고려한 실험들을 통해서 확인해야 할 것으로 예상한다. 또한, 이번 연구에서 사용한 영기선 이중차분이 아닌 단기선 이중차분을 통해서도 잡음을 도출할 수 있다. 이러한 경우에는, 다중경로 오차항의 제거에 적용한 방법에 따라 이 연구와 다른 결론이 나올 수 있다는 점을 유의해야 한다.
이 연구에서는 이중차분 코드의사거리 관측값에 대한 종합적인 분석을 통해서 수신기조합에 따라 달라지는 잡음의 특성들이 각각 측위 오차와 연관이 있음을 보였다는 것에 의의가 있다. 이를 통해서, 이중차분 잡음을 모델링하거나 줄임으로써 측위 성능이 향상될 수 있을 것으로 기대한다. 그러나, 분석이 GPS L1, GLONASS G1, Galileo E1에 국한되어 있으며, 동종의 수신기 조합에 대한 분석이 이루어지지 않았다는 한계점이 있다. 또한, 잡음의 모델링이 실질적으로 측위 성능을 향상에 기여하는지에 대하여 심층적인 연구가 추가로 필요하다.
향후 연구에서는 더 많은 항법위성군과 다양한 대역의 코드 의사거리와 반송파 위상에 대한 광범위한 분석이 필요하며, 동종의 수신기 조합이 가질 수 있는 잡음의 패턴과 유형에 대한 분석이 수행되어야 할 것이다. 또한, 잡음 유형들을 모델링함으로써 실질적으로 측위 성능향상에 기여할 수 있는지 구체적으로 검토해야 할 필요성이 있다.
최종적으로, 이번 연구는 다양한 가격대와 성능을 가진 수신기들의 조합과 코드 의사거리 이중차분 잡음 특성을 이해하는데 기여하고, 잡음과 측위 오차를 모델링할 수 있는 가능성을 제시함으로써, 정밀 GNSS 측위 분야에 기여할 수 있을 것으로 기대한다.
This work is supported by the Korea Agency for Infrastructure Technology Advancement grant funded by the Ministry of Land, Infrastructure and Transport (RS-2022-00141819, Development of Advanced Technology for Absolute, Relative, and Continuous Complex Positioning to Acquire Ultra-precise Digital Land Information).
Conceptualization, B.-G. Park and K.-D. Park; Formal analysis, B.-G. Park; Investigation, B.-G. Park; Methodology, B.-G. Park and K.-D. Park; Software, B.-G. Park; Supervision, K.-D. Park; Visualization, B.-G. Park; Writing – original draft, B.-G. Park; Writing – review & editing, B.-G. Park and K.-D. Park.
The authors declare no conflict of interest.
Allan, D. W. & Barnes, J. A. 1981, A Modified “Allan variance” with Increased Oscillator Characterization Ability, In Proceedings of the 35th Annual Frequency Control Symposium, Philadelphia, PA, 27-29 May 1981, pp.470-475. https://doi.org/10.1109/FREQ.1981.200514
Egea-Roca, D., Arizabaleta-Diez, M., Pany, T., Antreich, F., Lopez-Salcedo, J. A., et al. 2022, GNSS User Technology: State-of-the-Art and Future Trends, IEEE Access, 10, 39939-39968. https://doi.org/10.1109/ACCESS.2022.3165594
Hofmann-Wellenhof, B., Lichtenegger, H., & Wasle, E. 2008, GNSS – Global Navigation Satellite System: GPS, GLONASS, Galileo and more (Morlenbach: Strauss GmbH)
IEEE 1998, IEEE Standard Specification Format Guide and Test Procedure for Linear, Single-Axis Interferometric Fiber Optic Gyros, In IEEE Std 952-1997, 1-84. https://doi.org/10.1109/IEEESTD.1998.86153
Inside GNSS, Point One Navigation Expands Polaris Location Services to South Korea [Internet], cited 2024 Jan 25, available from: https://insidegnss.com
Kaplan, E. D. & Hegarty, C. J. 2006, Understanding GPS: principles and applications, 2nd ed. (Boston: Artech House Inc.)
Kawamoto, S., Takamatsu, N., & Abe, S. 2023, RINGO: A RINEX pre-processing software for multi-GNSS data, Earth Planets Space, 75, 54. https://doi.org/10.1186/s40623-023-01811-w
Kersten, T. & Paffenholz, J-A. 2020, Feasibility of Consumer Grade GNSS Receivers for the Integration in Multi-Sensor-Systems, Sensors, 20, 2463. https://doi.org/10.3390/s20092463
Misra, P. & Enge, P. 2006, Global Positioning System: Signals, Measurements, and Performance, 2nd ed. (Lincoln, MA: Ganga-Jamuna Press)
Niu, X., Chen, Q., Zhang, Q., Zhang, H., Niu, J., et al. 2014, Using Allan variance to analyze the error characteristics of GNSS positioning, GPS Solution, 18, 231-242. https://doi.org/10.1007/s10291-013-0324-x
Prochniewicz, D., Kudrys, J., & Maciuk, K. 2022, Noises in Double-Differenced GNSS Observations, Energies, 15, 1668. https://doi.org/10.3390/en15051668
Riley, W. J. & Howe, D. A. 2008, Handbook of frequency stability analysis (Boulder, CO: National Institute of Standards and Technology)